9.5. Теплопроводность плоской однослойной стенки

Рассмотрим плоскую однородную стенку толщиной δ, выполненную из материала, коэффициент теплопроводности которого λ не зависит от температуры. Левая поверхность стенки поддерживается при заданной постоянной по высоте стенки температуре t_ст1, правая – при более низкой, но тоже постоянной температуре t_ст2.

Т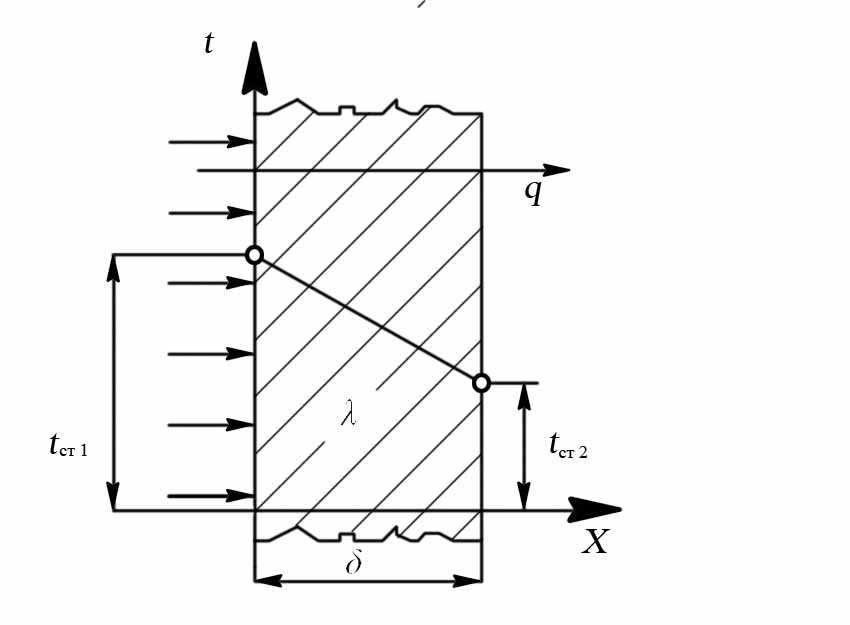 емпература стенки будет меняться только по её толщине, в направлении оси х (рис. 9.4.), т. е. температурное поле будет одномерным, а градиент температуры будет равен .

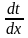Рис. 9.4. Плоская однослойная стенка

Найдём плотность теплового потока через заданную стенку и установим характер изменения температуры по толщине стенки.

Уравнение Фурье для одномерного температурного поля будет:

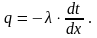
Чтобы проинтегрировать это уравнение, разделим переменные:

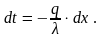
После интегрирования получим уравнение температурного поля для λ = const

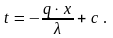^(9.16)

Чтобы найти постоянную интегрирования, используем известные значения температур: при х = 0, t = t_ст1 , а при х = δ, t = t_ст2.

Отсюда с = t_ст1, а следовательно, уравнение (9.16) будет иметь вид:

Решая уравнение относительно q, получаем:

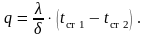(9.17)

Плотность теплового потока в плоской стенке прямо пропорциональна коэффициенту теплопроводности, перепаду температур и обратно пропорциональна толщине стенки.

В формуле (9.17) считается, что λ не зависит от температуры. Если λ зависит от температуры то вычисляется среднее значение коэффициента теплопроводности по выражению:

где λ₁ – коэффициент теплопроводности при температуре t_ст1;

λ₂ – коэффициент теплопроводности при температуре t_ст2.

Изменение температуры по толщине стенки описывается уравнением (9.16). Подставляя в него выражение для q из (9.17) и значение с = t_ст1, получим:

Температура по толщине однородной стенки изменяется по закону прямой линии.

9.6. Теплопроводность плоской многослойной стенки

В практике технических расчётов чаще встречаются многослойные плоские стенки. При условии плотного прилегания отдельных слоёв решение задачи теплопроводности, полученное для однослойной плоской стенки, можно распространить и на многослойную стенку.

Для примера рассмотрим задачу о теплопроводности плоской трёхслойной стенки (рис. 9.5.).

Рис. 9.5. Плоская многослойная стенка

Каждый из слоёв состоит из однородного материала с коэффициентом теплопроводности каждого слоя λ₁, λ₂, λ₃. Известны температуры наружных поверхностей многослойной стенки t_ст1 и t_ст4 и толщина каждого слоя δ₁, δ₂, δ₃. Предположим, что температуры t_ст1 и t_ст4 постоянны, т. е. рассматриваем опять одномерную задачу; тогда постоянной и одинаковой для всех слоёв будет и плотность теплового потока. Требуется определить величину q и температуры соприкасающихся поверхностей слоёв t_ст2 и t_ст3, которые по условиям задачи неизвестны.

Согласно закону Фурье плотность теплового потока через каждый из слоёв можно записать так:

Имеем три уравнения с тремя неизвестными:

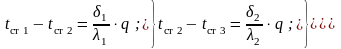(9.18)

Сложим левые и правые части уравнений (9.18):

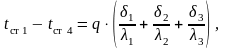
откуда:

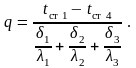(9.19)

Теперь, зная q, из уравнений (9.18) легко найти интересующие нас значения промежуточных температур t_ст2 и t_ст3:

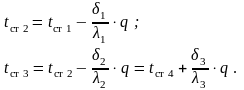
Очевидно, что если стенка будет иметь n слоёв, то:

(9.20)

Величины 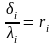называются частными тепловыми (термическими) сопротивлениями теплопроводности, а

(9.21)

общим тепловым (термическим) сопротивлением теплопроводности.

Теперь можно записать формулу (9.20) в таком виде:

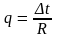(9.22)

Следовательно, плотность теплового потока через плоскую многослойную стенку пропорциональна разности температур на наружных поверхностях и обратно пропорциональна тепловому сопротивлению, равному сумме тепловых сопротивлений отдельных слоёв.

Температура в каждом слое стенки при λ = const меняется линейно. Следовательно, для многослойной стенки температурная кривая представляет собой ломаную линию.

Тангенс угла наклона каждого отрезка представляет собой градиент температуры в переделах данного слоя, значение которого можно найти из уравнения (9.16), если продифференцировать его:

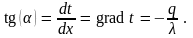(9.23)

Это уравнение показывает, что линия t = t (x) расположена тем круче, чем больше плотность теплового потока через стенку и чем меньше коэффициент теплопроводности материала стенки.

В многослойной стенке величина q одинакова для всех слоев. В этом случае угол наклона температурной линии тем ближе к 90°, чем меньше λ. Так, в примере на рис. 9.5. принято, что λ₃ < λ₁ < λ₂.