9.2. Температурное поле. Градиент температуры
Температурным полем называется совокупность значений температуры в каждый момент времени во всех точках рассматриваемого пространства. Если температура постоянна во времени, то поле называется стационарным или установившимся. Если же температура во времени меняется, то поле называется нестационарным (неустановившимся).
Температура может быть функцией трёх, двух и одной координат. В соответствии с этим различают трёх-, двух-, и одномерные температурные поля.
Математически нестационарное трёхмерное температурное поле, в общем случае задаётся уравнением, связывающим значение температуры в каждой точке тела со значением координат этой точки в данный момент времени и имеет вид1:
t = t (x,y,z,τ), (9.1)
где τ – время;
а стационарного поля:
t = t (x,y,z). (9.2)
Поверхности, представляющие собой геометрическое место точек с одинаковой температурой, называют изотермическими поверхностями, а линии пересечения изотермической поверхности с плоскостью – изотермами (рис. 9.1.).
В окрестности данной точки температура изменяется во всех направлениях, не совпадающих с касательной к изотерме. При этом наиболее резкое изменение температуры имеет место в направлении по нормали к изотермической поверхности.
Рис. 9.1. Температурное поле. Удельный тепловой поток, градиент температуры
Градиент температуры. Производная температуры по нормали к изотермической поверхности называется градиентом температуры:
(9.3)
Эта величина является вектором, направленным по нормали к изотермической поверхности в сторону увеличения температуры (см. рис. 9.1.).
Градиент температуры характеризует интенсивность изменения температуры в направлении нормали. Интенсивность изменения температуры в произвольном направлении меньшая, чем в направлении нормали, и равна проекции на это направление:
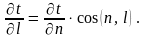
9.3. Тепловой поток. Плотность теплового потока. Закон Фурье
9.3.1. Тепловой поток
Количество
тепла, проходящее через данную поверхность
в единицу времени, называется тепловым
потоком Q,
Вт
.
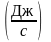Количество тепла, через единицу
поверхности в единицу времени, называется
плотностью
теплового потока или
удельным тепловым потоком и характеризует
интенсивность теплообмена.
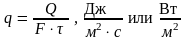(9.4)
Плотность теплового потока q, направлена по нормали к изотермической поверхности в сторону, обратную градиенту температуры, т. е. в сторону уменьшения температуры.
Если известно распределение q по поверхности F, то полное количество тепла Qτ, прошедшее через эту поверхность за время τ, найдется по уравнению:
(9.5)
а тепловой поток:
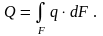(9.5')
Если величина q постоянна по рассматриваемой поверхности, то:
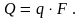(9.5")
9.3.2. Закон Фурье
Этот закон устанавливает величину теплового потока при переносе тепла посредством теплопроводности. Французский ученый Ж. Б. Фурье в 1807 году установил, что плотность теплового потока через изотермическую поверхность пропорциональна градиенту температуры:
(9.6)
Знак минус в (9.6) указывает, что тепловой поток направлен в сторону, обратную градиенту температуры (см. рис. 9.1.).
Плотность теплового потока в произвольном направлении l представляет проекцию на это направление теплового потока в направлении нормали:
