
- •Термодинамика и теплопередача. Учебное пособие
- •Раздел III. Теплопередача
- •Содержание
- •Раздел III
- •Тема 9. Основные положения. Теплопроводность тел при стационарном режиме
- •Тема 10. Теплообмен конвекцией. Конвективный теплообмен
- •Тема 11. Теплообмен излучением
- •Тема 12. Теплообменные аппараты
- •Тема 13. Методы тепловой защиты
- •Основные условные обозначения
- •Индексы
- •Предисловие
- •Раздел III теплопередача
- •Тема 9. Основные положения. Теплопроводность тел при стационарном режиме
- •9.1. Основные задачи теории теплообмена. Виды переноса тепла
- •9.2. Температурное поле. Градиент температуры
- •9.3. Тепловой поток. Плотность теплового потока. Закон Фурье
- •9.3.1. Тепловой поток
- •9.3.2. Закон Фурье
- •9.3.3. Коэффициент теплопроводности
- •9.4. Дифференциальное уравнение теплопроводности
- •9.5. Теплопроводность плоской однослойной стенки
- •9.6. Теплопроводность плоской многослойной стенки
- •9.7. Теплопроводность цилиндрической однослойной стенки
- •9.8. Теплопроводность цилиндрической многослойной стенки
- •9.9. Контактное тепловое сопротивление
- •9.10. Теплопроводность тел с внутренними источниками тепла
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Решение
- •Проверьте, как Вы усвоили материал
- •Тема 10. Теплообмен конвекцией. Конвективный теплообмен
- •10.1 Физические основы процесса
- •10.2.Дифференциальны уравнения конвективного теплообмена
- •10.3. Основы теории подобия процессов теплообмена
- •10.3.1 Основные понятия и определения теории подобия
- •10.3.2 Применение теории подобия к теплоотдаче
- •10.3.3 Критерии подобия процессов конвективного теплообмена.
- •10.3.4. Теоремы подобия
- •10.4. Моделирование физических явлений.
- •10.5. Определяющая температура
- •10.6. Конвективный теплообмен при вынужденном внешнем обтекании тел
- •10.6.1. Картина процесса.
- •10.6.2. Плотность теплового потока и уравнения подобия.
- •10.6.3 Особенности теплоотдачи при обтекании криволинейных поверхностей.
- •10.6.4. Теплоотдача с боковой поверхности вращающегося диска.
- •10.7. Конвективный теплообмен при вынужденном течении в каналах
- •10.7.1. Особенности теплоотдачи в каналах.
- •10.7.2. Плотность теплового потока; уравнения подобия.
- •10.8. Теплопередача
- •Проверьте, как Вы усвоили материал
- •Тема 11. Теплообмен излучением
- •11.1. Основные понятия
- •11.2. Закон Стефана-Больцмана
- •11.3. Закон Кирхгофа
- •11.4. Защитные экраны
- •11.5. Теплообмен в замкнутой полости
- •11.6. Излучение газов и паров
- •11.7. Излучение пламени
- •11.8. Расчёты при лучистом теплообмене
- •11.9. Лучисто-конвективный теплообмен
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Задача 11.4.
- •Решение
- •Решение
- •Проверьте, как Вы усвоили материал
- •Тема 12. Теплообменные аппараты
- •12.1. Основные типы теплообменных аппаратов
- •12.2. Анализ процесса в рекуперативном теплообменном аппарате
- •12.3. Эффективность теплообменника и способы её повышения
- •Примеры решения задач
- •Решение
- •Решение
- •Решение
- •Принципиальная схема лабораторной установки
- •Решение
- •Проверьте, как Вы усвоили материал
- •Тема 13. Методы тепловой защиты
- •13.1. Конвективное охлаждение
- •13.2. Пористое охлаждение
- •13.3. Заградительное (плёночное) охлаждение
- •13.4. Тугоплавкие теплозащитные покрытия
- •13.5. Уносимые теплозащитные покрытия
- •1 3.6. Применение методов тепловой защиты в охлаждении лопаток турбин гтд
- •Проверьте, как вы усвоили материал
- •Заключение
- •Список использованной литературы
- •Приложение
- •Извлечения из гост 8.417 – 2002
- •Единицы величин
- •Область применения
- •Нормативные ссылки
- •Определения
- •4. Общие положения
- •5. Единицы международной системы единиц (си)
- •Международная стандартная атмосфера (мса) гост 4401–81 (фрагмент)
- •Теплофизические величины
12.2. Анализ процесса в рекуперативном теплообменном аппарате
Различают конструктивный и проверочный тепловой расчёт теплообменного аппарата. Цель конструктивного расчёта состоит в определении величины рабочей поверхности теплообменника, которая является исходным параметром при его проектировании. При этом должно быть известно количество передаваемой теплоты или массовые расходы теплоносителей и изменение их температуры.
Проверочный расчёт выполняется для теплообменника с известной величиной поверхности. Цель расчёта состоит в определении температур теплоносителя на выходе из теплообменника и количество передаваемой теплоты.
На рис. 12.4. изображены температурные поля прямоточного (рис. 12.4, а) и противоточного (рис. 12.4, б) теплообменников. Индексами 1 и 2 отмечаются температуры и другие параметры соответственно горячего и холодного теплоносителя. Одним и двумя штрихами отмечаются параметры теплоносителя на входе и выходе из теплообменного аппарата.
В основе анализа процесса и расчёта рекуперативного теплообменного аппарата лежат два уравнения:
уравнение теплового баланса
Q1 = Q2 + ∆Q (12.1)
уравнение теплопередачи
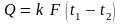 (12.2)
(12.2)
где Q1 и Q2 – количество тепла, отдаваемое горячим и воспринимаемое холодным теплоносителем; ∆Q – потери тепла в окружающую среду; k – коэффициент теплопередачи; t1, t2 – температуры теплоносителей; F – площадь поверхности теплообмена.
Изменение температуры теплоносителей в теплообменнике.
Учитывая, что
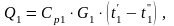
![]() (12.2′)
(12.2′)
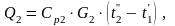 (12.3′)
(12.3′)
и пренебрегая потерями тепла в окружающую среду, уравнение (12.1) можно записать в виде
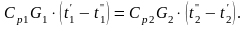 (12.3)
(12.3)
Здесь
G1,
G2,
Ср1,
Ср2
-
расходы и теплоёмкости горячего
(первого) и холодного (второго)
теплоносителей;
 —
их температуры на входе и выходе
теплообменника.
—
их температуры на входе и выходе
теплообменника.
Введём понятие водяного эквивалента W = Ср G. С учётом этого уравнение (12.3) примет вид:
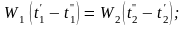
преобразуя, получим выражение
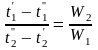 (12.4)
(12.4)
Отсюда следует, что изменение температуры теплоносителей в теплообменнике обратно пропорционально их водяным эквивалентам. При равенстве водяных эквивалентов изменение температуры теплоносителей одинаково. На рис. 12.4 показан характер изменения температуры теплоносителей в прямоточном (12.4, а) и в противоточном (12.4, б) теплообменных аппаратах при различных соотношениях водяных эквивалентов.
Площадь
рабочей поверхности теплообменника.
Исходя из того, что разность температур
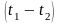 изменяется по длине теплообменного
аппарата, уравнение теплопередачи для
него запишется в виде
изменяется по длине теплообменного
аппарата, уравнение теплопередачи для
него запишется в виде
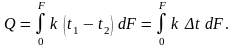
Величину ∆t в теории теплообменных аппаратов называют температурным напором. В расчетах используется величина среднего температурного напора, равного:
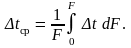
С учётом этого, а также принимая k = const, уравнение теплопередачи можно записать в виде
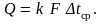 (12.5)
(12.5)
Это выражение является исходным для определения площади рабочей поверхности теплообменника:
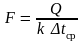 (12.6)
(12.6)
Таким образом, площадь рабочей поверхности, а следовательно, и масса теплообменника при данной величине Q зависят от коэффициента теплопередачи и среднего температурного напора.
а
б
F
F
F
F
F
F

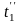

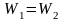
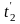
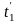
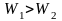

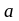
Рис.12.4. Схемы изменения температур t1, t2 в зависимости от схемы движения теплоносителей и значений водяных эквивалентов: а – прямоток, б – противоток
Определение F составляет основную задачу проектировочного расчета теплообменника. Обычно величина Q в этом случае бывает задана, а средний температурный напор может быть найден, если известны расходы теплоносителей, их температуры на входе и выбрана схема течения (см. ниже).
Коэффициент теплопередачи (см. тему 10) зависит от параметров теплопередающей стенки (λ, δ) и коэффициентов теплоотдачи. Последние, при неизменном режиме течения, определяются формой и размерами каналов и скоростью движения теплоносителей. При проектировании теплообменника эти величины выбирают из условия обеспечения наиболее эффективных характеристик аппарата (вопрос 12.3).
Средний температурный напор. Получим выражение среднего температурного напора для наиболее простого случая – прямоточной схемы теплообменника.

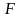
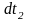
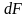
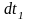
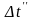

Рис. 12.5. К расчёту среднего температурного напора
Количество тепла, передаваемое в единицу времени через элементарный участок рабочей поверхности dF (рис. 12.5), составляет
dQ = k ∆t dF . (12.7)
При этом температура теплоносителей на участке dF изменяется на величины dt1,dt2, определяемые выражениями:
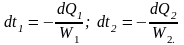
Уменьшение температурного напора равно:
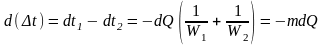 ,
,
где
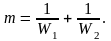 (12.8)
(12.8)
Подставляя в предпоследнее выражение dQ из (12.7) и разделяя переменные, получим
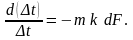
Интегрируем, считая k и m постоянными; тогда
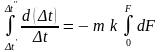
или
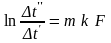 .
(12.9)
.
(12.9)
В этих выражениях (см. рис. 12.5)
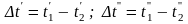 .
.
Выразим величины m из уравнений (12.2´) и (12.8) и kF из (12.5)


Подставляя
эти значения в уравнение (12.9) и разрешая
его относительно
 ,
получим:
,
получим:
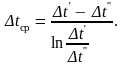 (12.10)
(12.10)
Значение
![]() определенное
по формуле (12.10), носит название
среднелогарифмического температурного
напора. Это выражение применимо также
и для противоточной схемы теплообменника.
Однако в этом случае величины
определенное
по формуле (12.10), носит название
среднелогарифмического температурного
напора. Это выражение применимо также
и для противоточной схемы теплообменника.
Однако в этом случае величины
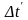
![]() и
и

![]() (см. рис. 12.4, б) определяются как
(см. рис. 12.4, б) определяются как
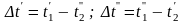
Если разница между и невелика, то величина среднего температурного напора может быть определена как среднеарифметическое крайних напоров:
 (12.11)
(12.11)
В
диапазоне
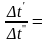 0,6
– 1,67 отличие между среднеарифметическим
и среднелогарифмическим температурными
напорами не превышает 3%.
0,6
– 1,67 отличие между среднеарифметическим
и среднелогарифмическим температурными
напорами не превышает 3%.
Аналитическое
определение среднего температурного
напора для более сложных схем движения
теплоносителей приводит к громоздким
формулам. С целью упрощения расчетов
результаты решения для наиболее часто
встречающихся схем теплообменных
аппаратов представлены в справочной
литературе в виде графиков. В этом случае
определение среднего температурного
напора сводится к следующему. Вначале
по формуле (12.10) определяют
средний температурный напор
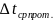 ,
cчитая рассматриваемую схему как чисто
противоточную. Затем рассчитывают
вспомогательные величины Р
и
R:
,
cчитая рассматриваемую схему как чисто
противоточную. Затем рассчитывают
вспомогательные величины Р
и
R:
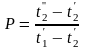

Используя график для рассматриваемой схемы теплообменного аппарата, находят величину поправочного коэффициента ε∆t и определяют средний температурный напор по формуле
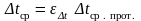
Зависимости коэффициента ε∆t от Р и R для двух типов теплообменных аппаратов приведены на рис. 12.6.
Определение конечных температур теплоносителей и интервалов теплового потока.
Задача
определения конечных температур
теплоносителей
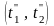 и теплового потока Q
является целью поверочного расчёта
выполненного или спроектированного
теплообменника. При решении этой задачи
известны площадь рабочей поверхности,
коэффициент
теплопередачи, водяные эквиваленты
теплоносителей и их начальные температуры.
и теплового потока Q
является целью поверочного расчёта
выполненного или спроектированного
теплообменника. При решении этой задачи
известны площадь рабочей поверхности,
коэффициент
теплопередачи, водяные эквиваленты
теплоносителей и их начальные температуры.
Рассмотрим приближённое решение задачи, считая, что температуры теплоносителей в теплообменнике изменяются по линейному закону. Тогда средний температурный напор как для прямоточной, так и противоточной схем на основании (12.11) определится по формуле
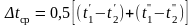 (12.12)
(12.12)
а

б
Рис.12.6. Графические зависимости ε∆t = f(P, R) для определения поправки ε∆t
При отсутствии потерь тепла в окружающую среду (∆Q =0) тепловой поток равен:
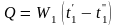 (12.13)
(12.13)
или
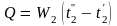 (12.14)
(12.14)
Выражая
отсюда значения
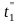 и
и
 подставляя их в уравнение (12.12),
получим:
подставляя их в уравнение (12.12),
получим:

На основании выражения (12.5)
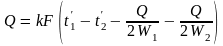 (12.15)
(12.15)
Решая (12.15) относительно Q, получим формулу для определения полного теплового потока:
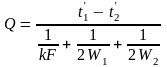 (12.16)
(12.16)
По
найденному значению Q
далее из (12.13) и (12.14) определяются
конечные температуры
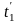 и
и
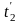
![]() .
Из (12.16), в частности, видно, что если при
изменении режима работы системы, в
которую включён теплообменник,
изменяется расход одного или обоих
теплоносителей, то тепловой поток и
конечные температуры будут также
изменяться. Это обусловлено изменением
соответствующих водяных эквивалентов
и коэффициентов теплоотдачи.
.
Из (12.16), в частности, видно, что если при
изменении режима работы системы, в
которую включён теплообменник,
изменяется расход одного или обоих
теплоносителей, то тепловой поток и
конечные температуры будут также
изменяться. Это обусловлено изменением
соответствующих водяных эквивалентов
и коэффициентов теплоотдачи.
В теории теплообменных аппаратов используется понятие степени регенерации:
 (12.17)
(12.17)
где Qmax – максимально возможное количество тепла, которое может быть передано от одного теплоносителя другому в единицу времени.
Нетрудно установить, что
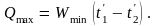 (12.18)
(12.18)
где Wmin – меньший из водяных эквивалентов. Отметим, что определение ϭрег, вытекающее из (12.17) и (12.18), является наиболее общим. Степень регенерации, рассмотренная в теме 5, является частным случаем при W1 = W2.
Подставив в (12.17) значение Qmax из (14.18) и Q из формулы (14.16), считая в последней один из водяных эквивалентов максимальным, а другой минимальным, получим
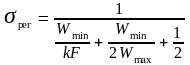 (12.19)
(12.19)
из (12.19) следует, что
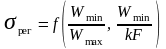 (12.20)
(12.20)
Формула (12.16), а следовательно, и формула (12.19) являются приближенными и применимыми в области параметров, где выполняется условие (12.11). При проведении точных расчетов в общем случае для определения теплового потока можно исходить из условия (12.17), т.е.
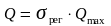
Значения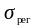 в
виде функции (12.20) для различных схем
теплообменников заранее рассчитаны
и приводятся в специальной литературе.
На рис. 12.7 приведены такие данные для
прямоточной (а) и противоточной (б)
схем.
в
виде функции (12.20) для различных схем
теплообменников заранее рассчитаны
и приводятся в специальной литературе.
На рис. 12.7 приведены такие данные для
прямоточной (а) и противоточной (б)
схем.

Рис. 12.7. Зависимости степени регенерации для различных схем теплообменников
