10.3.4. Теоремы подобия

Первая теорема подобия (Теорема Ньютона). Первая теорема подобия формулируется так:

У подобных явлений одноименные критерии подобия численно одинаковы. Следовательно, в подобных процессах конвективного теплообмена при вынужденном движении критерии Nu, Pe, Re, M этих подобных процессов имеют численно одинаковые значения. Данное условие записывается так:

Nu = idem, Pe = idem, Re = idem, M = idem (10.14)

Имея в виду, что Pe = Re · Pr, условие (10.14) можно заменить условием

Nu = idem, Pr = idem, Re = idem, M = idem (10.15)

В отдельных частных случаях условия подобия упрощаются. Например, при малых скоростях движений газа (M<0,3), когда можно пренебречь сжимаемостью газа, отпадает условие M = idem.

Поэтому подобные процессы конвективного теплообмена при малых скоростях движения характеризуются условием

Nu = idem, Re = idem, Pr = idem (10.16)

Таким образом, равенство одноименных критериев подобия является следствием подобия явлений. Вместе с тем, это обстоятельство может служить и признаком по которому устанавливается наличие или отсутствие подобия физических явлений.

Вторая теорема подобия. Выше отмечалось, что теория подобия позволяет решать вопрос о рациональном обобщении результатов исследований. Решение этой задачи базируется на второй теореме подобия. Согласно этой теореме решение системы уравнений, описывающих какое-либо явление, может быть представлено в виде зависимости между критериями подобия, получаемыми из данной системы уравнений.

Рассмотрим это положение на примере конвективного теплообмена. Введем в (10.10) и (10.11) критерии подобия, тогда

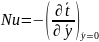(10.17)

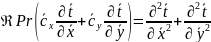(10.18)

Таким образом, конвективный теплообмен описывается безразмерными уравнениями (10.17) и (10.18), в которых безразмерные величины можно рассматривать как новые переменные; их две группы:

- независимые, составленные только из заданных размерных величин: Re, Pr, ;

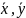- зависимые, включающие в себя искомые величины: Nu, .

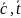Критерии подобия, являющиеся независимыми переменными (Re, Pr и др.), называют определяющими критериями, а зависимые – определяемыми.

Очевидно, что искомая (определяемая) величина является функцией независимых (определяющих) величин, входящих в систему уравнений. Поэтому на основе сказанного можно записать

Nu = f (Re, Pr, ). (10.19)

А для заданной точки пространства –

Nu = f (Re, Pr ). (10.20)

Уравнения (10.19) и (10.20), представляющие собой функциональную связь между критериями подобия, называются уравнения подобия (критериальными уравнениями). В частности, уравнения (10.19) и (10.20) представляют собой уравнения подобия стационарного конвективного теплообмена при вынужденном движении.

Таким образом, мы показали, что результаты исследований можно представить в виде уравнений подобия, а не только в виде функциональной связи между размерными величинами. Число критериев подобия меньше числа размерных величин, из которых они составлены. Поэтому число независимых переменных в уравнениях подобия меньше, чем в уравнениях, выражающих связь между размерными величинами, характеризующими процесс. Следовательно, результаты исследования конвективного теплообмена при вынужденном движении можно представить в виде зависимости (10.20). Если бы результаты такого исследования представлялись в виде функциональной зависимости между размерными величинами, характеризующими данный процесс, то полученное уравнение должно было бы иметь вид (10.2). Сравнение (10.2 и 10.20) позволяет сделать вывод, что использование критериальных уравнений подобия существенно упрощает постановку исследований и их обобщение.