10.3.2 Применение теории подобия к теплоотдаче

Критерии подобия. Критериями подобия (числами подобия) называются безразмерные комплексы, составленные из размерных величин, характеризующих данное явление. Вывод критериев подобия для каждого явления производится из анализа уравнений, описывающих это явление. Рассмотрим это на примере процесса конвективного теплообмена при стационарном движении.

Для простоты рассмотрим двухмерную задачу. Пусть имеются две подобные системы (см. рис. 10.4). В каждой из них теплообмен описывается уравнениями теплоотдачи (10.4) и переноса тепла (10.7). Приведем их к безразмерной форме. Для этого выберем масштабы приведения: для линейных величин – характерный размер l (например, длину поверхности теплообмена), для скоростей – скорость невозмущенного (набегающего) потока c₀, для температур – температурный напор ΔT.

Обозначим безразмерные величины

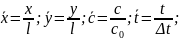
Тогда уравнения (10.4) и (10.7) с учётом того, что рассматривается стационарный процесс, принимают вид:

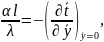(10.10)

(10.11)

У подобных явлений, как указывалось, безразмерные поля одноименных величин тождественны. Поэтому и уравнения, их описывающие, т.е. уравнения (10.10) и (10.11), должны быть одинаковы. Последнее возможно, если каждый из безразмерных комплексов, входящих в эти уравнения, имеет одно и то же значение для всех подобных явлений, т.е.

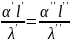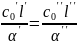, . (10.12)

Здесь индексами (Ι) и (ΙΙ) обозначены величины, соответственно относящиеся к первой и второй системам (см. рис.10.3). Аналогичный анализ уравнения движения (уравнение Навье-Стокса), который мы здесь опускаем, приводит при вынужденном движении к дополнительным условиям:

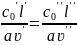(10.13)

а при больших скоростях движения также к условию

(10.13ʹ)

Безразмерные комплексы типа (10.12), 10.13) и (10.13ʹ) являются критериями (числами) подобия. Критериям присваиваются имена выдающихся учёных, их обозначают двумя первыми буквами выбранного имени.

10.3.3 Критерии подобия процессов конвективного теплообмена.

1. Критерий Рейнольдса –

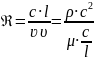
Этот критерий определяет соотношение между силами инерции и силами вязкости в потоке теплоносителя. Это следует из формулы, в которой числитель определяет силу инерции, пропорциональную скоростному напору, а знаменатель – силу вязкости (внутреннего трения). При малых числах Re преобладающими силами являются силы вязкости, при больших – силы инерции. В зависимости от соотношения этих сил меняются и условия течения жидкости, в частности режим течения; так как, при Re < Re_кр – течение ламинарное, а при Re > Re _кр – течение турбулентное. Таким образом, число Рейнольдса характеризует условия течения жидкости (газа) и в конечном итоге поле (распределение) скорости в потоке.

Критерий Re является определяющим критерием для конвективного теплообмена при вынужденном движении жидкости (газа), так как здесь задается скорость движения. Для процессов конвективного теплообмена при свободном движении скорость движения не задается, значит критерий Re является неопределяющим в процессах, связанных с естественной конвекцией.

2. Критерий Грасгофа – безразмерный комплекс определяется выражением:

Gr =

Где l – характерный линейный размер; Δt = (t_ст – t_ж); β – коэффициент объемного расширения при нагревании в 1К; для идеального газа β = l/Т

Критерий Грасгофа характеризует интенсивность свободного движения, которая зависит от соотношения между подъемной силой, обусловленной различием плотности в отдельных точках изотермического потока, и сил вязкого трения. Этот критерий является определяющим в процессах, связанных с естественной конвекцией.

3. Критерий Прандтля составлен из физических параметров вещества и является физическим параметром.

Pr =

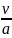
Данный критерий характеризует соотношение между скоростью обмена механической энергией между частицами жидкости (за счёт вязкости) и скоростью обмена тепловой энергией (за счёт температуропроводности – а). Критерий Pr – критерий физических средств вещества и является определяющим критерием. Для некоторых капельных жидкостей (вода, масло, глицерин) с ростом температуры в величина Pr сильно уменьшается. Критерий Прандтля жидких металлов меняется в пределах Pr = 0,005…0,05; также низкие значения критерия Pr жидких металлов в основном объясняются их высокой теплопроводностью. Многим нефтепродуктам свойственны, наоборот, высокие значения Pr из-за высокой вязкости.

Для газов значение критерия Прандтля практически не зависит от температуры, а зависит только от числа атомов в молекуле:

- для одноатомных газов Pr = 0,65;

- для двухатомных газов Pr = 0,72;

- для трехатомных газов Pr = 0,8;

- для многоатомных газов Pr = 1,0;

4. Критерий Пекле – безразмерный комплекс определятся выражением:

Pe = ,

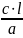Где а – коэффициент температуропроводности. Представим критерий Пекле следующим образом:

Pe =

Где Pr = v/а – Критерий Грандтля;

Re = c·l/v – критерий Рейнольдса.

5. Критерий Нуссельта –

Nu =

Этот критерий представляет собой безразмерный коэффициент теплоотдачи и характеризует соотношение между интенсивностью теплоотдачи α, и интенсивностью теплопроводности в пограничном слое потока жидкости (λ_ж). Коэффициент теплоотдачи α всегда является величиной искомой, неизвестной в задачах о конвективном теплообмене. Следовательно, критерий Nu является неопределяющим критерием и его значение всегда зависит от значения всех определяющих критериев

Nu = f (Re, Gr, Pr).

Это уравнение называется критериальным уравнением конвективного теплообмена. Обычно из двух гидродинамических критериев Re и Gr в уравнении останется лишь один:

- при естественной конвекции – критерий Gr;

- при вынужденной конвекции - критерий Re;

6. Критерий Маха – M =

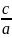
Характеризует сжимаемость газового потока; поэтому его изменение влияет на процессы теплообмена при значениях М, когда эта сжимаемость ощутима.