4. Кернеулік векторының ағыны

Ауданды нормаль бағытында тесіп өтетін күш сызықтарының санын немесе және векторларының скаляр көбейтіндісін кернеулік векторының агыны деп атайды.

Бipтeктi өpicтe нормалі өpic векторы -мен бүрыш жасайтын жазық бет орналаскан дейік (4-сүрет).Сонда, ағынның анықтамасы бойынша Ф_Е мынаған тең болады:

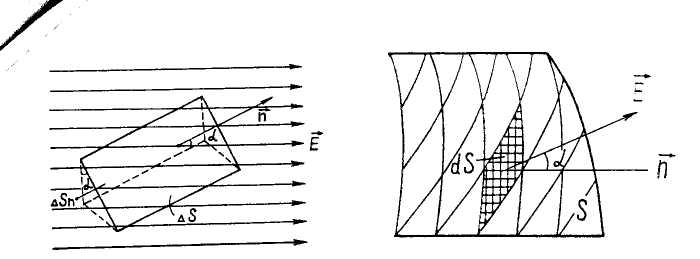
4-сурет

Ф_Е ^{= =} Е S cos =E_n S (4.1) Мұндағы E_n=Е cos -E-нің нормалі бағытына проекциясы. Егер бүрышы сүір (cos >0) болса, онда ағын оң болады, егер бүрышы доғал (cos <0) болса, онда ағын тepic болады. Егер бет тұйық болса, онда нормальдің оң бағыты ретінде сыртқы нормальдің бағыты таңдалып алынады.

5. Остроградский — Гаусс теоремасы

Өpicтi +q нүктелік заряды тудырады дейік. Мұның айналасынан кез келген r радиүсты S₁ сферасын сызайық. Осы сфералық беттен өтетін векторы ағынын есептейік.

Ф_Е = (5.1)

Егер де бет зарядты камтымайтын болса (5-cypeттeгi S_В -6eтi), онда бетке eнeтiн (кipeтiн) және одан шығатын күш сызықтарының саны бірдей болады, ал тұйық беттен өте­тін толық ағын Ф_Е =0.

S 6eтi q_1, q₂, ...,q_N зарядтарының жиынтығын қамтитын болсын. Өpiстiң сүперпозициясы бойынша

S 6eTi q_u q₂, ..., ^лгзарядта-рыньщ жиынтырын камтитын болсын. ©piCTin сүперпозиңия-сы бойынша

және

N

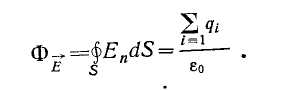
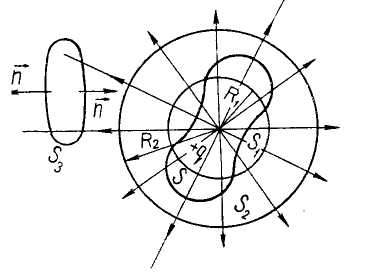
5-сурет

Тұйық бет арқылы өтетін кернеүлік векторының ағыны осы беттің iшiндe болатын зарядтардың алгебралық қосындысына пропорционал болады. Бұл тұжырым Остроградский — Гаүсс теоремасы деп аталады.

Остроградский — Гаүсс теоремасы арқылы кейбір дербес жағдайлардағы электр өpiciн есептеп табайық.

а) Бipкeлкi зарядталған шексіз беттің электр өpici.

(5.3)

б) Әр аттас зарядталган ( + және — ; шексіз параллель екі жазықтықтың өpici. Бұл жағдайда зарядтар пластинкалардың ішкі беттерінде болады.

Е= (5.4)

Кез келген формалы зарядты есептеуге F=Eq формүласы пайдаланылады. Сонда (5.4) -өрнегін ескерсек,

F= - (5.5)

Бұдан қысымға арналған мына өрнек шығады

P= (5.6)

6. Электр өрісінің потенциалы

Сан мәні зарядты өpicтiң берілген нүктесінен шексіздікке дейін қозғаған кезде істелетін жұмыстың осы зарядтың шамасына катынасына тең болатын энергетикалық сипаттаманы электростатикалық өрістің потенңиалы деп атайды;

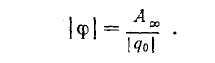
Бұл анықтама теория жүзіндегі анықтама болып табылады. Зарядты жер бетінен өpicтiң берілген нүктесіне дейін қозғаған кезде істелетін жұмыстың осы зарядтың шамасы­на катынасын электростатикалық өрістің потенңиалы деп атайды.

Зарядты өpicтiң потенңиалы ₁ болатын нүктесіен потенңиа­лы ₂ болатын нүктесіне дейін қозғаған кезде істелетін жұмыс­тың осы заряд шамасына қатынасын потенңиалдар айырымы (ф₁ —ф₂) деп атайды:

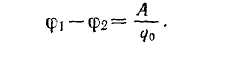(6.2)

7. Нүктелік заряд тудыратын өрістің потенциалы

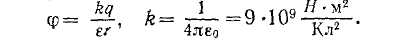
-дің r-ге тәүелділігінің графигі гиперболамен кескінделеді. Зарядтың таңбасына тәүелсіз r кезде болады. Егер q>0 болса, r 0 кезде болады. Егер де q<0 болса, онда r 0 кезде болады.