Данное пособие является третьим из 3-х частей I раздела (теории статистики) и посвящено теме 4: Выборочное наблюдение. Статистические методы изучения взаимосвязей (12 часов).

Практическое занятие № 13 и № 14: Выборочное наблюдение

План

1. Понятие выборочного наблюдения и его преимущества.

2. Генеральная и выборочная совокупности, их обобщающие характеристики.

3. Методы, виды и способы формирования выборочных совокупностей.

4. Ошибки выборочного наблюдения.

5. Определение необходимой численности выборки.

6. Расчет ошибок выборки при различных способах отбора (задача).

7. Расчет необходимой численности выборки (задача).

Вопросы для обсуждения

1. Какое наблюдение называется выборочным?

2. В чем преимущества выборочного наблюдения перед сплошным?

3. Какие вопросы необходимо решить для проведения выборочного наблюдения?

4. Почему при выборочном наблюдении неизбежны ошибки и как они классифицируются?

5. Каковы условия правильного отбора единиц совокупности при выборочном наблюдении?

6. Как производятся собственно-случайный, механический, типический и серийный отборы?

7. В чем различие повторной и бесповторной выборки?

8. Что представляет собой средняя ошибка выборки (для средней и доли)?

9. По каким расчетным формулам находят средние ошибки выборки (для средней и доли) при повторном и бесповторных отборах?

10. Что характеризует предельная ошибка выборки и по каким формулам она исчисляется (для средней и доли)?

11. Что показывает коэффициент доверия?

12. В чем значение теоремы Чебышева — Ляпунова для решения задач выборочного наблюдения?

13. Какими способами осуществляется распространение результатов выборочного наблюдения на всю совокупность?

14. Зачем и как исчисляются предельные статистические ошибки выборки (для средней и доли)?

15. По каким формулам определяется необходимая численность выборки, обеспечивающая с определенной вероятностью заданную точность наблюдения?

Примеры решения типовых задач

Пример 1. Из партии электроламп взята 20%-ная случайная бесповторная выборка для определения среднего веса спирали. Результаты выборки следующие:

Вес, мг	38-40	40-42	42-44	44-46
Число спиралей	15	30	45	10

Определить с вероятностью 0,95 доверительные пределы, в которых лежит средний вес спирали, для всей партии электроламп.

Решение

Доверительные интервалы для генеральной средней с вероятностью Р:

- средний уровень признака по выборке:

;

При вероятности Р = 0,95 t = 1,96 (по таблице).

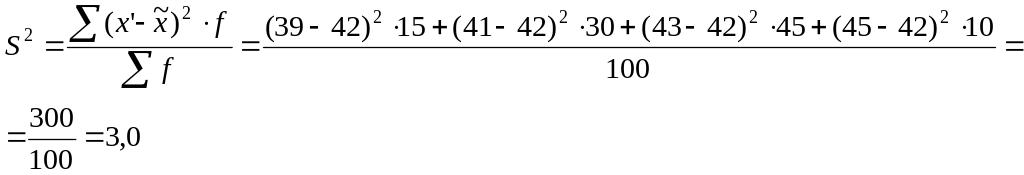
Доверительные интервалы для генеральной средней с вероятностью Р = 0,95:

42,0 - 0,3 ≤ ≤. 42,0 +0,3; 41,7 мг. ≤ ≤. 42,3 мг.

Пример 2. На заводе электроламп из партии продукции в количестве 1600 шт. ламп взято на выборку 1600 шт. (случайный, бесповторный отбор), из которых 40 шт. оказались бракованными.

Определить с вероятностью 0,997 пределы, в которых будет находиться процент брака для всей партии продукции.

Решение.

Определяется доля бракованной продукции по выборке:

, или 2,5%.

При вероятности Р = 0,997 t = 3,0 (по таблице);

Размер предельной ошибки

, или 1,1%.

Доверительные интервалы для генеральной доли с вероятностью Р = 0,997

, ;

1,4% ≤ р ≤ 3,6%.

Пример 3. По городской телефонной сети в порядке случайной выборки (механический) отбор произвели 100 наблюдений и установили среднюю продолжительность одного телефонного разговора 5 мин. при среднем квадратическом отклонении 2 мин.

Какова вероятность того, что ошибка репрезентативности при определении средней продолжительности телефонного разговора не превысит 18 сек.?

Решение

По условию задачи известны:

объем выборки - п = 100;

выборочная средняя - = 5 мин.;

выборочное среднее квадратическое отклонение -S=2 мин.;

предельная ошибка выборки - = 18 сек. = 0,3 мин.

;

Затем по таблице на основе значения t определяется вероятность того, что ошибка не превысит заданной величины.

При t = 1,5 вероятность Р = 0,866.

Пример 4. На основе выборочного обследования в отделении связи города предполагается определить долю писем частных лиц в общем объеме отправляемой корреспонденции. Никаких предварительных данных об удельном весе этих писем в общей массе отправляемой корреспонденции не имеется.

Требуется определить численность выборки, если результаты выборки дать с точностью до 1% и гарантировать это с вероятностью 0,95.

Решение

По условию задачи известны:

размер допустимой (предельной) ошибки - Д/> 1%, или 0,01;

принятая вероятность - Р = 0,95;

при Р = 0,95 t = 1,96 (см. приложение 3).

Необходимая численность выборки:

Так как значение w не дано, то следует ориентироваться на наибольшую дисперсию, которой соответствует значение w = 0,5.

.

Таким образом, чтобы с заданной точностью определить долю частных писем в общем объеме отправляемой корреспонденции, необходимо в порядке случайной выборки отобрать 9604 письма.

Пример 5. На предприятии в порядке случайной бесповторной выборки было опрошено 100 рабочих из 1000 и получены следующие данные об их доходе за октябрь:

Месячный доход, руб.	600 - 1000	1000- 1400	1400- 1800	1800-2200
Число рабочих	12	60	20	8

Определить: 1) среднемесячный размер дохода у работников данного предприятия, гарантируя результат с вероятностью 0,997; 2) долю рабочих предприятия, имеющих месячный доход 1400 руб. и выше, гарантируя результат с вероятностью 0,954; 3) необходимую численность выборки при определении среднего месячного дохода работников предприятия, чтобы с вероятностью 0,954 предельная ошибка выборки не превышала 50 руб.; 4) необходимую численность выборки при определении доли рабочих с размером месячного дохода 1400 руб. и выше, чтобы с вероятностью 0,954 предельная ошибка не превышала 4%.

Решение

1. Доверительный интервал среднего размера месячного дохода работников предприятия:

Средний месячный доход по выборке

Предельная ошибка выборки .

При вероятности Р = 0,997 t = 3,0

; ;

2. w - доля рабочих, имеющих размер месячного дохода 1400 руб. и выше:

Предельная ошибка доли

При вероятности Р = 0,954 t = 2.

Доверительные интервалы для генеральной доли:

; 0,28 - 0,085 ≤ р ≤ 0,28 + 0,085;

0,195 ≤ р ≤ 0,365.

3. Необходимая численность выборки для определения среднего месячного дохода определяется по формуле

.

По условию задачи известны:

при вероятности Р = 0,954 t=2

= 50 руб.; S² = 93184 (по данным предыдущей выборки).

чел.

4. Необходимая численность выборки для определения доли рабочих, имеющих доход 1400 руб. и выше, определяется по формуле

.

По условию задачи известны:

∆р= 2%, или 0,02; при вероятности Р = 0,954 t = 2;

w = 0,28 (по данным предыдущей выборки).

чел.

Пример 6. Операция шлифования при обработке детали № 312 производится в цехе на трех станках. Для определения процента брака для всей партии продукции, выработанной за день, проведена расслоенная (типическая) 10%-ная выборка. Отбор деталей из выработки каждого станка - случайный бесповторный; объем выборки пропорционален размеру выпуска. На первом станке было обработано 1700 деталей, на втором - 2000, на третьем - 1800. Число забракованных деталей в выборке: по первому станку - 2, по второму - 3, по третьему - 3.

Определить: 1) доверительные интервалы, в которых с вероятностью 0,95 заключен процент брака для всей партии продукции: 2) вероятность того, что процент брака для всей партии продукции отличается от полученного по выборке не более чем на 0,6.