Федеральное агентство по образованию Российской Федерации

Филиал «Севмашвтуз» государственного образовательного учреждения высшего профессионального образования «Санкт – Петербургский государственный морской технический университет»

в г. Северодвинске

Факультет: № 4

Кафедра: № 12

Лабораторная работа

Определение модуля Юнга методом изгиба и модуля сдвига с помощью пружинного маятника

Северодвинск

2007

Лабораторная работа ФМ - 19

Определение модуля Юнга методом изгиба и модуля сдвига с помощью пружинного маятника

1. Цель и метод работы

Цель - научиться определять модуль Юнга методом изгиба и модуль сдвига двумя способами: с помощью пружинного маятника и методом растяжения пружины.

2. Основные теоретические положения

Все реальные тела деформируемы. Под действием приложенных сил они меняют свою форму или объем. Такие изменения называются деформациями. В случае твердых тел различают два предельных случая: деформации упругие и деформации пластические.

Упругими называют деформации, исчезающие после прекращения действия приложенных сил.

Пластическими или остаточными деформациями называют такие деформации, которые сохраняются в теле, по крайней мере частично, и после прекращения действия приложенных сил. На пластических деформациях основана холодная обработка металлов – штамповка, ковка…

Является ли деформация упругой или пластической – это не только зависит от материала, но и от приложенных сил. Если сила не превосходит известной величины, называемой пределом упругости, то деформация будет упругой. Если же она превосходит этот предел, то деформация будет пластической.

Одной из причин деформации тел является действие силы тяготения. Если тело неподвижно, то вес (сила давления на опору) численно равна силе тяжести. Реакция опоры, как и вес тела, относится к упругим силам.

Под влиянием груза Р проволка или стержень длинною L и поперечного сечения S растягивается (или укорачивается) на величину ∆l. По закону Гука (сила упругости прямо пропорциональна абсолютной деформации):

, (1)

где α – коэффициент упругости при растяжении (сжатии), или коэффициент продольного удлинения (сжатия). Модуль упругости при растяжении, или модуль Юнга, равен:

(2)

Модуль Юнга численно равен напряжению, при действии которого длина тела при деформации удвоилась бы. Измеряется он в паскалях (1 Па = 1 Н/м²).

Р ассмотрим деформацию сдвига. Возьмем однородное тело, имеющее форму параллелепипеда и приложим к его противолежащим граням силы F₁ и F₂ (F_{1 =} F_{2 =} F), направленные параллельно этим граням (Рис.1.)

Если действие сил будет распределено равномерно по всей поверхности соответствующей грани, то в любом сечении, параллельном этим граням, возникнет тангенциальное напряжение τ = F/S, где S площадь грани. Под действием напряжений тело деформируется так, что одна грань сместится относительно другой на некоторое расстояние a. Если тело мысленно разбить на элементарные параллельные рассматриваемым граням слои, то каждый слой окажется сдвинутым относительно соседних с ним слоев. По этой причине деформация такого вида получила название сдвига.

При деформации сдвига любая прямая, первоначально перпендикулярная к слоям, повернется на некоторый угол ψ. В качестве характеристики деформации сдвига берется величина

,

называемая относительным сдвигом (смысл a и b виден из рис.1.) При упругих деформациях угол ψ бывает очень мал. Поэтому можно положить

tgψ = ψ. Следовательно относительный сдвиг γ оказывается равным углу сдвига ψ.

Относительный сдвиг пропорционален тангенциальному напряжению

Коэффициент G зависит только от свойств материала и называется модулем сдвига. Он равен такому тангенциальному напряжению, при котором угол сдвига оказался бы равным 45⁰ (tgψ = 1), если бы при столь больших деформациях не был превзойден предел упругости. Измеряется G, как и E, в паскалях.

3. Вывод рабочей формулы

Если прямой упругий стержень неподвижно закрепить одним концом в твердой стене, а другой конец нагрузить грузом Р, то этот конец опустится, т.е. стержень согнется (рис.2). Легко понять, что при таком изгибе верхние слои стержня будут растягиваться, нижние сжиматься, а некоторый средний слой, который называется нейтральным, сохранит длину и только претерпит искривление.

Перемещение y , которое получает свободный конец стержня, называется стрелой прогиба. Стрела должна быть тем больше, чем больше нагрузка, и, кроме того, она должна зависеть от формы и размеров стержня и от его модуля упругости.

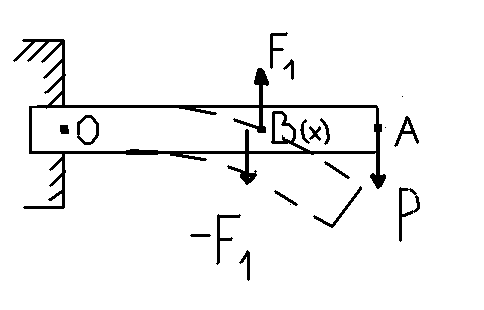
Рис. 2

Поместим начало координат в точку О, где нейтральная линия балки пересекается с плоскостью стены. Через произвольную точку В(х) с координатой (х = ОВ) проведем нормальное сечение. Для равновесия необходимо, чтобы сила F₁ действующая на часть ВА со стороны ОВ была направлена в верх и равнялась Р. Вместе с Р она образует пару сил с моментом инерции:

, где l – длинна балки.

Момент сил также равен:

, где a – ширина, b – высота пластины.

Таким образом

Интегрируя это уравнения получим:

Полагая х = l , находим стрелу прогиба:

(3)

В случае если стержень будет обоими концами свободно положен на твердые опоры и нагружен в середине весом Р (см. рис. 3) , то стрела прогиба найдется также из уравнения (3), но только вместо Р надо будет подставить Р/2, а вместо l – l/2.

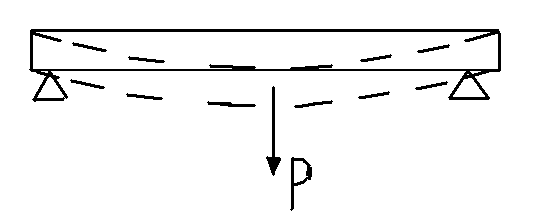
Рис. 3

В самом деле, в этом случае каждая из опор оказывает на стержень противодействие Р/2, тогда как средняя часть остается горизонтальной.

Следовательно, в этом случае стрела прогиба будет равна:

, откуда модуль Юнга

(4)

Модуль сдвига определить по формуле

, (5)

где Т – период колебаний, m – масса груза, D – средний диаметр пружины (определить при помощи штангенциркуля), d – диаметр проволоки, N – число витков пружины.

4. Описание опытной установки

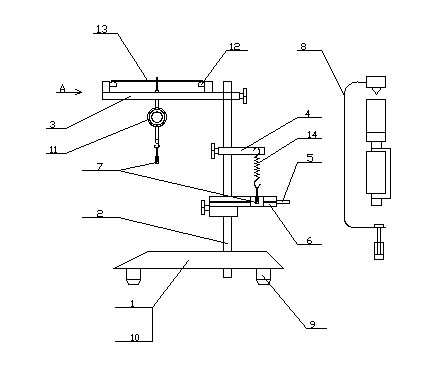
Рис. 3

Установка представлена на рис.3 и включает в свой состав:

1. – основание 1,

2. – вертикальную стойку 2,

3. – кронштейны 3, 4 и 5 (кронштейн 5 для установки фотодатчика)

4. – фотодатчик 6,

5. – наборный груз 7,

6. – устройство для нагружения образца 8,

7. – основание 1 снабжено тремя треугольными опорами 9 и зажимом 10 для фиксации вертикальной стойки 2,

8. – вертикальная стойка 2 выполнена из металлической трубы,

9. – на кронштейне 3 закреплены часовой индикатор 11 и две призматические опоры 12, на которые устанавливается исследуемый образец 13 (пластина),

10. – кронштейн 4 имеет узел крепления вертикально подвешиваемых сменных пружин 14,

11. – кронштейны 3 и 4 имеют зажимы для крепления на вертикальной стойке 2,

12. – кронштейн 5 имеет зажим для крепления на вертикальной стойке 2 и элементы фиксации фотодатчика,

13. – устройство 8 нагружения образца представляет собой скобу с призматической опорой и узлом подвески наборного груза.

14. – наборный груз 7 подвешивается или на устройство 8 или на одну из пружин 14.