2.3.2 Расчет нижней части ступенчатой колонны.

Сечение нижней части колонны проектируем сквозным, состоящим из двух ветвей, соединенных раскосной решеткой с дополнительными стойками. Высота сечения h_H = 1500 мм. Принимаем сечение подкрановой ветви из прокатного двутавра, сечение наружной ветви – из двух уголков, соединенных листом (см. рисунок 2.1). Раскосы и стойки решетки колонны проектируем из одиночных уголков.

Подкрановую ветвь колонны рассчитываем по усилиям М₁ = -1151,6 кНм, N₁ = -2188,2 кНм, наружную – по усилиям М₂ = 1270,1 кНм, N₂ = -2106,6 кНм.

Определяем ориентировочное положение центра тяжести колонны. Принимаем z₀ = 5 см, h₀ = h_H - z₀ = 150 – 5 = 145 см.

см;

см.

Усилие в подкрановой ветви:

кН.

Усилие в наружной ветви:

кН.

Определяем требуемую площадь ветвей и компонуем их сечение. Для листового и фасонного проката толщиной 2 - 20 мм из стали класса С235

R_y = 230 МПа. Предварительно задаемся  = 0,8.

Для подкрановой ветви см²;

для наружной ветви см².

Из условия обеспечения общей устойчивости колонны из плоскости действия момента (из плоскости рамы) высоту сечения нижней части колонны назначают в пределах (1/20 – 1/30)  Н_Н, что соответствует гибкости  = 60…100. При Н_Н = 1200 см высота сечения будет от 1200 / 2 = 60 см до 1200 / 30 = 40 см. Назначаем высоту сечения нижней части колонны 50 см.

Принимаем для подкрановой ветви двутавр № 50 ГОСТ 8239-89: А_В1 = 100 см² , I_Ix = 1043 см⁴, I_y = 39727 см⁴, i_x1 = 3,23 см, i_y = 19,9 см.

Сечение наружной ветви принимаем из двух уголков, соединенных вертикальным листом (рисунок 2.1). Учитывая условия размещения сварных швов и удобство сварки, назначаем лист сечением h  t = 460  10 мм. Требуемая площадь уголка А_тр = (А_В2 – h  t) / 2 = (107,6 – 46,0  1,0) / 2 = 30,8 см². Принимаем два уголка 160  10 ГОСТ 8509-93 с площадью сечения 31,4 см².

Площадь сечения наружной ветви А_В2 = 31,4  2 + 46,0  1,0 = 108,8 см².

Расстояние от наружной грани до центра тяжести ветви:

z₀ = S₀ / A_B2 = 46,0  1,0  0,5 + 2  31,4  1 + 4,3 / 108,8 =3,3 см.

Моменты инерции сечения наружной ветви:

I_x2 = 2  (774 + 31,4  2,03²) + 46,0  1,0  2,77² = 2160 см²,

I_y = 1,0  46,0³ / 12 + 2  774 + 31,4  20,7² = 36569 см⁴.

Радиусы инерции сечения наружной ветви:

см; см.

Общая площадь сечения колонны А_В1 + А_В2 = 100 + 108,8 = 208,8 см².

Расстояние между осями ветвей h₀ = h_H - z₀ = 150 – 3,3 = 146,7 см.

Расстояние от центра тяжести сечения до центральных осей ветвей:

y₁ = A_B2  h₀ / A = 108,8  146,7 / 208,8 = 76,4 см,

y₂ = h₀ - y₁ = 146,7 – 76,4 = 70,3 см.

Уточняем усилия в ветвях колонны с учетом фактических y₁ и y₂.

кН,

кН.

Проверяем устойчивость ветвей колонны из плоскости рамы (относительно оси y-y) при расчетной длине =1200 см.

Подкрановая ветвь: гибкость ветви _y = / i_y = 1200 / 19,9 = 60,3; коэффициент продольного изгиба  = 0,809;

МПа  R_y  _c = 230  1.0 = 230 МПа.

Наружная ветвь: _y = / i_y = 1200 / 18,3 = 65,6;  = 0,783;

МПа  R_y  _c = 230  1,0 = 230 МПа.

Максимальная гибкость колонны из плоскости рамы не превышает предельно допустимой:

_y = 65,6  _u = 180 – 60   = 180 – 60  1,0 = 120;

где  =  / (R_y _c) = 230 / (230  1,0) = 1,0  0,5.

Из условия равноустойчивости подкрановой ветви в плоскости и из плоскости рамы определяем требуемое расстояние между узлами решетки:

_x1 = _B1 / i_x1 = _y _Bi = _y  i_x1 = 60,3  3,23 = 194,8 см.

Угол наклона раскосов к горизонтали принимается в пределах 40⁰ - 50⁰.

Назначаем расстояние между узлами решетки _B1 = _B2 = 1580 мм (см. рисунок 2.1), разделив нижнюю часть колонны на целое число панелей, и приняв высоту траверсы в узле сопряжения верхней и нижней частей колонны h_s = 800 мм, что в пределах рекомендуемых значений h_s = ( 0,5…0,8)  h_H.

Проверяем устойчивость ветвей колонны в плоскости рамы (относительно осей 1-1 и 2-2) при их расчетной длине, равной расстоянию между узлами решетки.

Подкрановая ветвь: ;  = 0,860;

МПа  R_y  _c = 230  1,0 = 230 МПа.

Наружная ветвь: ;  = 0,915;

МПа  R_y  _c = 230  1,0 = 230 МПа.

Устойчивость ветвей нижней части колонны обеспечена.

В составных стержнях с решетками гибкость отдельных ветвей между узлами должна быть не более 80, что в нашем случае выполняется.

Рассчитываем элементы решетки подкрановой части колонны. Раскосы решетки рассчитывают на большую из поперечных сил: фактическую Q_max = 203,4 кН или условную Q_fic = 7,15 , которая может быть определена после проверки устойчивости колонны в целом как единого стержня. Приближенно при R_y = 230 МПа Q_fic  0,25  А = 0,25  208,8 = 52,2 кН.

Приближенно при R_y = 200 МПа Q_fic = 0,2  А,

при R_y = 440 МПа Q_fic=0,6  А.

Для промежуточных значений R_y Q_fic определяется интерполяцией.

Усилие сжатия в раскосе

N_ = Q_max / (2  sin) = 203,4 / (20,691) = 147,2 кН,

где sin = h_H / _p = 150 / 217 = 0,691; _p = см;

 = 43,7⁰ – угол наклона раскоса.

Для сжатых элементов решетки из одиночных уголков, прикрепленных к ветви одной полкой коэффициент условий работы _с = 0,75.

Задаемся гибкостью раскоса см².

Принимаем уголок 110  8 ГОСТ 8509-93, А_p = 17,2 см², i_min = 2,18 см.

Расчетная длина раскоса _ef = _p = 217 см.

Гибкость раскоса _max = _ef / i_min = 217 / 2,18 = 99,5,  = 0,559.

Напряжение в раскосе

МПа  R_y  _c = 230  0,75 = 172,5 МПа.

Стойки решетки колонны рассчитываем на условную поперечную силу в наиболее нагруженной ветви колонны

кН.

Конструктивно стойки принимаем из углов 75  6 ГОСТ 8509-93,

А_с = 8,78 см², i_min = 1,48 см, _max = _ef / i_min = 150 / 1,48 = 101,4,  = 0,547.

Напряжения в стойке

МПа  R_y  _c = 230  0,75 = 172,5 МПа.

Проверяем устойчивость нижней части колонны в плоскости действия момента как единого стержня. Геометрические характеристики всего сечения:

I_x = I_x1 + A_B1 y₁² + I_x2 + A_B2 y₂² =1043 + 10076,4² +2160+108,870,3² =1124600 см⁴;

см.

Гибкость колонны в плоскости рамы _x = _x1 / i_x = 2094 / 73,4 = 28,5.

Приведенная гибкость

,

где ₁ =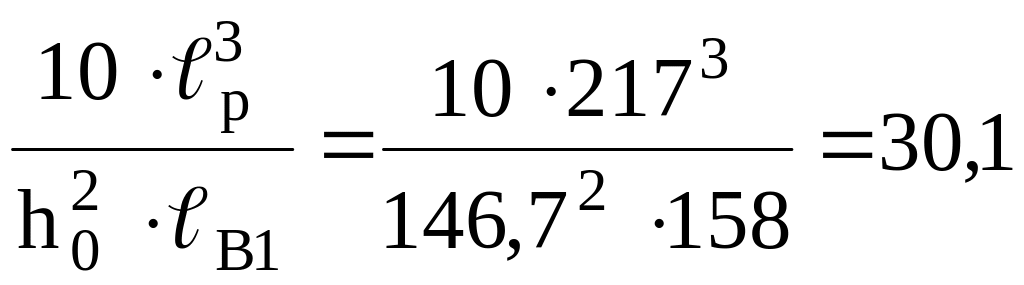 ; A_pI = 2  A_p = 2  17,2 = 34,4 см².

Условная приведенная гибкость

.

Для расчетной комбинации усилий, догружающих подкрановую ветвь,

N₁ = - 2188,2 кН; М₁ = - 1151,6 кНм;

; _е = 0,541;

МПа  R_y  _c = 230 МПа.

Для расчетной комбинации усилий, догружающих наружную ветвь,

N₂ = - 2106,6 кН; М₂ = 12700,1 кНм;

; _е = 0,522;

МПа  R_y  _c = 230 МПа.

Условная поперечная сила в нижней части колонны

кН  Q_max = 203,4 кН.

Устойчивость сквозной колонны как единого стержня из плоскости действия момента проверять не нужно, так как она обеспечена проверкой устойчивости отдельных ветвей.