2.2 Определение расчетных длин колонны

Расчетные длины для нижней и верхней частей колонны в плоскости рамы определяем по формулам (1.1)

где = H_H, = H_B.

Коэффициенты ₁ и ₂ определяются в зависимости от параметров n и ₁ по 2, пп. 4.8.

Соотношение погонных жесткостей верхней и нижней частей колонны

; ,

где  = N₁ / N₂ = 21,88 / 366,3 = 5,97 – соотношение усилий в нижней и верхней частях колонны.

Для однопролетной рамы с жестким сопряжением ригеля с колонной (верхний коней колонны закреплен только от поворота) 1, таблица 68, см. 2, пп. 4.8 ₁ = 1,745; ₂ = ₁ / ₁ = 1,745 / 0,389 = 4,49  3,0. Принимаем ₂ = 3,0.

Таким образом, для нижней части колонны

= 1,745  1200 = 2094 см;

для верхней

= 3,0  620 = 1860 см.

Расчетные длины из плоскости рамы для нижней и верхней частей колонны равны соответственно:

H_H = 1200 см; H_H - h_б = 620 – 165 = 455 см.

2.3 Расчет верхней части ступенчатой колонны

2.3.1 Подбор сечения верхней части колонны.

Верхнюю часть колонны принимаем из сварного двутавра высотой h_B = 1000 мм. Из условия устойчивости определяем требуемую площадь сечения. Для симметричного двутавра:

i_x  0,42h = 0,421000 = 24 см; _x  0,35h = 0,351000 = 35 см.

Условия гибкости стержня

где R_y = 230 МПа для листового проката толщиной 2 - 20 мм из стали С235.

Относительный эксцентриситет m_x = .

Примем приближенно А_f / A_W = 0,5, тогда коэффициент влияния формы сечения 1, таблица 73, см. п. 4.9 [2]   , Приведенный относительный эксцентриситет m_ef = m_x = 1,25  8,01 = 10,01.

По 1, таблица 74, см. п. 4.10 [2] при и m_ef = 10,01 коэффициент _е = 0,134.

Коэффициент условий работы для колонны _с = 1,0.

см².

Предварительно толщину полки принимаем t_f = 1,4 см.

Тогда высота стенки h_ef = h_w = h - 2t_f = 100 - 21,4 = 97,2 cм.

Определим требуемую толщину стенки из условия ее местной устойчивости при изгибе колонны в плоскости действия момента . Предельная условная гибкость стенки при m_x  1,0 и  2,0 1таблица 27*; см. п. 4.15 2

.

При но не более 3,1.

Требуемая толщина стенки см.

Примечание - Если толщина стенки принимается по данному условию, то в дальнейших расчетах вместо h_red следует принимать h_w и вместо А_red – А.

Поскольку сечение с такой толстой стенкой неэкономично, то стенку назначаем меньшей толщины, исключая из расчета ее неустойчивую часть. При этом из условия местной устойчивости стенки при изгибе из плоскости действия момента приближенно

см.

Принимаем t_w = 10 мм. Расчетная (редуцированная) высота стенки, включающая два участка стенки, примыкающих к полкам,

где ;

k = 1,2 + 0,15 (здесь при  3,5 принимать ). Требуемая площадь и ширина полки

А_f = ( А - h_red  t_w) / 2 = (118,9 – 42,5  1,0) / 2 = 38,2 см²;

B_f = А_f / t_f = 38,2 / 1,4 = 27,3 см.

Из условия устойчивости верхней части колонны из плоскости действия момента b_f  _y2 / 20 = 455 / 20 = 22,8 см.

Из условия местной устойчивости полки ,

где - величина свеса полки;

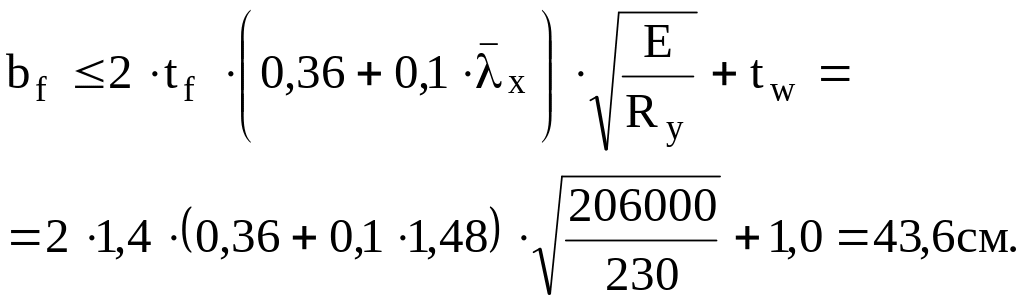
Принимаем b_f = 320 мм (рисунок 2.1).

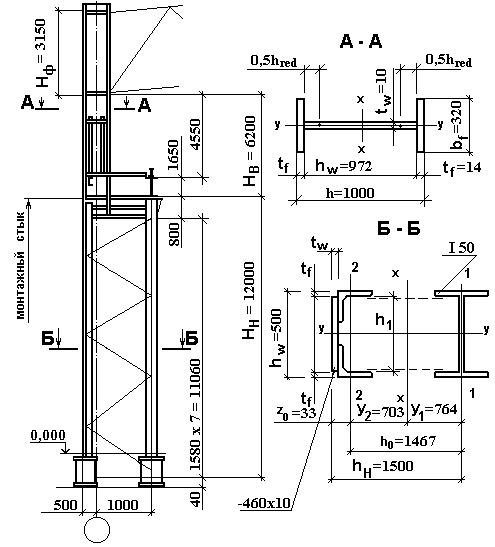
Рисунок 2.1 – Конструктивная схема и сечения колонны

Вычисляем геометрические характеристики сечения.

Полная площадь сечения

А = 2  b_f  t_f + h_w  t_w = 2  32  1,4  97,2  1,0 = 186,8 см².

Расчетная площадь сечения с учетом только устойчивой части стенки

А_red = 2  b_f  t_f + h_red  t_w = 2  32  1,4 + 42,5  1,0 = 132,1 см².

см⁴.

I_y = 2  t_f  b_f³ / 12 = 2  1,4  32³ / 12 = 7646 см⁴.

W_x = 2  I_x / h = 2  294300 / 100 = 5886 см³.

_х  W_x / A = 5886 / 186,8 = 31,5 см.

см.

см.

Проверяем устойчивость верхней части колонны в плоскости действия момента. Гибкость колонны _х = / i_x = 1860 / 39,7 = 46,9;

.

Так как незначительно отличается от предварительно принятой, то расчетную высоту стенки h_red можно не уточнять.

Относительный эксцентриситет

Так как A_f / A_w = 32  1,4 / (97,21,0) = 0,461  0,5, то коэффициент  = 1,25 1, таблица 73. m_ef =   m_x = 1,25  8,9 = 11,1; _e = 0,121.

Если m_ef  20, то расчет на устойчивость не требуется и колонну следует рассчитывать на прочность как сжато-изогнутый элемент.

МПа R_y  _e = 230  1,0 = 230 МПа.

Недонапряжение  5%.

Гибкость колонны в плоскости рамы не превышает предельно допустимой _х = 46,9  _u = 180 – 60   = 180 – 60  0,996 = 120,2,

где  =/(R_y _с) =229 / 230 = 0,996  0,5 (при   0,5 следует принимать  = 0,5).

Проверяем устойчивость верхней части колонны из плоскости действия момента. Гибкость колонны _y = / i_y = 455 / 6,4 = 71,1. Коэффициент продольного изгиба _y = 0,754 1, таблица 72); см. п. 4.6 1.

Максимальный момент в средней трети расчетной длины стержня (рисунок 2.2)

По модулю  кНм.

Рисунок 2.2 – К определению расчетного момента

Относительный эксцентриситет

Так как 5  m_max  10, то коэффициент с определяем по 1, формула 59.

При m_x  5 коэффициент с определяется по 1, формула 57

с =  / 1 + m_x,

при m_x  10 коэффициент с определяем по 1, формула 58

с = 1 / (1+ m_x  _y / _b).

При m_x = 5 1, таблица 10); см. п. 4.14 1,

 = 0,65 + 0,05  m_x = 0,65 + 0,05  5 = 0,9 (при m_x  1,  = 0,7).

Так как _y = 71,1  _c = 3,14  , то   1. При _y  _c →  = ,

где _с – коэффициент продольного изгиба в зависимости от _c).

с₅ =  / (1 +   m_x) = 1 / (1 + 0,95) = 0,182.

При m_x = 10, с₁₀ = 1 / 1 + m_x  _y / _b = 1 / (1 + 10  0,574 / 1,0) = 0,117,

где _b = 1,0 в большинстве случаев при проверке устойчивости колонн.

с = с₅  (2 – 0,2  m_x) + с₁₀  (0.2  m_x - 1) =

=0,182  (2 – 0,2  6,77) + 0,117  (0,2  6,77 -1) = 0,156.

При _y_c = 3.14 коэффициент с не должен превышать

,

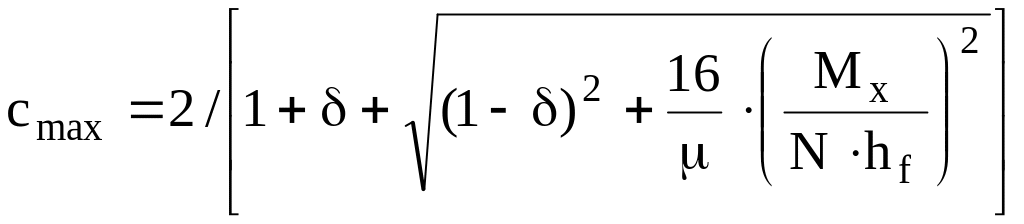где  = 4 / ;  = (J_x + J_y) / (A  h_f²);

 = 2 + 0,156  _y²  J_t / (A  h_f²); J_t = 0,433  b_i  t_i³;

здесь b_i и t_i – соответственно ширина и толщина листов, образующих сечение;

h_f – расстояние между осями поясов.

МПа.

Гибкость колонны из плоскости рамы не превышает предельно допустимой _y = 71,1  _u = 180 – 60   = 180 – 60  0,725 = 136,5,

где  =  / (R_y  _c) = 166,7 / 230 = 0,725  0,5.

Если в колонне имеется ослабление сечения или m_ef  20, то следует проверить прочность колонны с учетом развития пластических деформаций по формуле .

Проверяем местную устойчивость полки колонны.

Свес полки b_ef = (b_f - t_w) / 2 = (32 – 1,0) / 2 = 15,5 см.

Т. к.

,

то местная устойчивость полки обеспечена.

Проверяем местную устойчивость стенки при изгибе колонны из плоскости действия момента.

Наибольшие сжимающие напряжения на краю стенки:

МПа; напряжения на противоположном краю стенки:

МПа.

Средние касательные напряжения в стенке

МПа.

Коэффициент (с учетом знаков  и ₁).

При  = 1,79  1 наибольшее отношение h_ef / t_w определяем по формуле

 ,

где  = 1,4 (2 - 1)  τ /  = 1,4  (2  1,79 - 1) 16,1 / 189,1 = 0,308.

Принимаем (h_ef / t_w)_u = 113,7.

Так как h_ef / t_w = 97,2 / 1,0 = 97,2  (h_ef / t_w)_u = 113,7, то местная устойчивость стенки обеспечена.

При h_ef / t_w = 97,2  2,3 , стенку следует укреплять поперечными ребрами жесткости, расположенными на расстоянии (2,5 - 3)  h_ef, но не менее двух ребер в пределах верхней части колонны.

Ширина парных симметричных ребер

b_h  h_ef / 30 + 40 = 972 / 30 + 40 = 72,4 мм.

Принимаем b_h = 80 мм.

Толщина ребер t_s  2 b_h  мм.

Принимаем t_s = 6 мм.