4. Программирование алгоритмов циклической структуры.

Подготовка к работе

1. По указанной литературе изучить:

• организацию циклов с неизвестным и известным числом повторений;

• возможности языка C# для организации циклов с неизвестным числом повторений с помощью инструкции while… и do… while;

• возможности языка C# для организации циклов с известным числом повторений с помощью инструкции for.

2. Разработать алгоритмы решения задач в соответствии с заданием.

3. Составить программы решения задач.

Контрольные вопросы

1. Дайте понятие итерационного циклического процесса. Его отличия от цикла с заданным числом повторений.

2. Чем отличается алгоритмическая структура «ДО» от структуры «ПОКА»?

3. Каким оператором реализуется структура «ПОКА»? Привести формат его записи и пояснить, как с его помощью реализуется циклический процесс?

4. В какой структуре тело цикла может не выполниться ни разу? Пояснить почему.

5. Каким оператором реализуется структура «ДО»? Привести формат его записи пояснить, как с его помощью реализуется циклический процесс?

6. В какой структуре тело цикла будет выполнено ходя бы один раз? Пояснить почему.

7. Чем определяется условие выхода из цикла в структурах с известным и не известным числом повторений?

8. В каких случаях при решении циклических задач в теле цикла необходимо использовать составной оператор?

9. Для решения какого рода задач используются операторы с пред- и постусловиями?

10. Каковы преимущества использования операторов цикла в программе?

11. Когда используется инструкция цикла for? Какого типа должна быть переменная-счетчик?

12. Чем отличается инкрементный и декрементный варианты использования инструкций for?

13. Как организуется вычисление сумм?

14. Как организуется вычисление произведения?

15. Как организовать регулярные циклы с шагом отличным от единицы на языке C#?

Задание и порядок выполнения работы

1. Задача1 (2). Составить алгоритмы, написать программы, создать консольные приложения для вычисления на ПК значения функций, заданных в табл. 4.1 с использованием инструкции for.

На экран вывести значения вводимых исходных данных и полученные результаты, сопровождая их именами переменных. Ввести программу в редактор кода консольного приложения. Сохранить проекты решения Задач 1 и 2 в своей папке на диске D:\Temp\ …\ Prg\Р4\P4_1(2) под именами Z1 и Z2 соответственно в папках P4_1 и P4_2. Откомпилировать проекты, устранить ошибки. Запустить на исполнение, проанализировать результат вычисления и сделать выводы.

Таблица 4.1

N	Задача 1	Задача 2
	a = 2.5; b = 0.7; x = 2.1
1
2
3
4
5
6
7
8
9
10
11
12

3. Задача 3. Составить алгоритм, написать программу, создать консольное приложение для вычисления на ПК значения функции, заданной в табл. 4. 2.

Вычисление выполнить двумя способами:

а) используя инструкции while и б) используя инструкции do … while.

Сохранить как два отдельных проекта под именами Z3 и Z4, соответственно в папках P4_3 и P4_4 на диске D:\Temp\ …\ Prg\Р4\P4_3(4) соответственно в папках P4_3 и P4_4.

На экран вывести значения вводимых исходных данных и полученные результаты в виде таблицы. Таблицу оформить символами, например « * ». При заданном диапазоне изменения переменной x = [1 ÷ 4], с шагом 0,3 вариант вывода таблицы расчетных данных будет иметь вид:

Таблица

* * * * * * * * * * * * * * * * * *

* значение x * значение y *

* * * * * * * * * * * * * * * * * *

* 1.00 * 0.85 *

* * * * * * * * * * * * * * * * * *

* 1.30 * 0.56 *

* * * * * * * * * * * * * * * * * *

* . . . . . * . . . . . *

* * * * * * * * * * * * * * * * * *

* 4.00 * 0.91 *

* * * * * * * * * * * * * * * * * *

Символ « * » можно заменить на любой другой символ.

3. Запустить на исполнение, проанализировать результат вычисления и сделать выводы.

Таблица 4.2

№	Функции и условия	Данные	Диапазон аргумента
1		b=2	x = [1 ; 4] шаг=0.3
2		a=1.5	x = [0.5 ; 3] шаг=0.3
3		b=1.5	x = [1 ; 5] шаг=0.4
4		a=0.5	x = [-2 ; 3] шаг=0.4
5		a=3	x = [0 ; 5] шаг=0.5
6		a=2 b=5	x = [1 ; 5] шаг=0.5
7		a=1.65 b=5	x = [0 ; 5] шаг=0.5
8		a=2.3 b=-0.3	x = [1 ; 5] шаг=0.3
9		a=2.5 b=2.6	x = [2 ; 5] шаг=0.5
10		a=1.5 b=1.5	x = [0 ; 4] шаг=0.4
11		a=2 b=3	x = [1 ; 3] шаг=0.3
12		a=10	x = [-0.5 ; 3] шаг=0.3

5. Cкопировать все созданные проекты – папки P4_1 (2, 3,4) с их содержимым на свою Flash-память.

6. Завершить работу и подготовить отчет.

На защите уметь составлять программы по любому варианту заданий, приведенных в табл. 4.1 и 4.2.

Методические указания по выполнению задания

Задача 1. Используя оператор for, вычислить на ПК значение функции , при х=0.5. В приведенной формуле сомножитель 5x² не зависит от параметра n, поэтому расчетную формулу можно упростить как: . Параметром цикла здесь является аргумент n и накопление суммы будет происходить по (1/n).

П ри вычислении конечных сумм и произведений искомый результат формируется постепенно. При вычислении суммы сначала вычисляется S₁ = S₀ + S(n₁), во втором повторе цикла эта сумма увеличивается на второе слагаемое и получается S₂ = S₁ + S(n₂), в третьем повторе - на третье слагаемое S₃ = S₂ + S(n₃) и т.д. Здесь S₀ - начальное значение суммы и т.к. S₁ должна быть равна S(n₁) , то S₀ = 0.

При вычислении произведения сначала вычисляется Р₁ = Р₀*P(n₁), затем Р₂ = Р₁*P(n₂) и т.д. Здесь Р₀ - начальное значение произведения и т.к. Р₁ должно быть равно P(n₁) , то Р₀ = 1.

Поскольку сомножитель 5х² не зависит от параметра n его можно вынести за знак суммы, и в тело цикла это произведение включать не следует. Тем самым сокращается время исполнения программы. Блок-схема алгоритма решения задачи (Рис. 4.1) и соответствующая ей программа будут иметь вид:

Результаты работы программы:

Рис. 4.1. Блок- схема алгоритма задачи 1

З адача 2. Вычислить на ПК значения функции

Результаты работы программы:

Рис. 4.2. Блок схема алгоритма задачи 2.

Задача 3. Используя операторы while…do и do…, while вычислить значения функции

, в диапазоне изменения x от 0 до 3 с шагом 0.5.

При решении данной задачи можно использовать алгоритмы циклической структуры "ДО" и "ПОКА". Параметром данного цикла является х, причем при каждом повторном вычислении его значение следует увеличивать на величину шага. По условию задачи начальным значением х примем 0, а конечным значением – 3.

Рассмотрим разные варианты решения этой задачи.

| x= 0.00 | y= 1.00 |

| x= 0.50 | y= 0.88 |

| x= 1.00 | y= 0.54 |

| x= 1.50 | y= 1.00 |

| x= 2.00 | y= 0.91 |

| x= 2.50 | y= 0.60 |

| x= 3.00 | y= 0.14 |

------------------------

| x= 0.00 | y= 1.00 |

------------------------

| x= 0.50 | y= 0.88 |

------------------------

| x= 1.00 | y= 0.54 |

------------------------

| x= 1.50 | y= 1.00 |

------------------------

| x= 2.00 | y= 0.91 |

------------------------

| x= 2.50 | y= 0.60 |

------------------------

| x= 3.00 | y= 0.14 |

------------------------

Задания для самостоятельного решения.

Задача4. Составить блок-схему и написать программу, вычисляющую сумму (Задача4), заданную по варианту, приведенному в таблице 4.3. Для решения задачи использовать оператор for…

Таблица 4.3

N	Задача4	Задача5	Е	х
1			0,005	1,2
2			0,002	0,9
3	.		0,003	1,4
4			0,004	0,7
5			0,001	0,6
6			0,005	0,8
7			0,004	1,5
8			0,002	1,2
9			0,003	0,9
10			0,001	1,4
11			0,004	0,7
12	y = x10 + 2x9 + 3x8 + ... + 10x + 11 , где х=0,5		0,005	0,9

* Проанализировать шаг изменения х_i и составить два регулярных цикла с шагом dx1 и dx2.

Задача5. Составить блок-схему и написать программу, вычисляющую заданную функцию (Задача5), приведенную по варианту в таблице 4.3, разложив ее в ряд с заданной точностью Е. Определить минимально необходимое число членов ряда, сами члены ряда и их сумму, обеспечивающие представление функции с заданной точностью.

Методические указания по выполнению задачи 5

Представить функцию в виде ряда с точностью 0,001 при х=0,8.

Как известно из математики функцию y(x) можно разложить в ряд и рассчитать путем сложения первых нескольких n членом ряда. Например, y= a₀ + a₁ + a₂ + a₃ + a₄ + …+ a_n + a_n+1. . .

Функция e^-x может быть разложена в ряд Тейлора. Ряд сходящийся и рассчитывается путем сложения n членов ряда. Для организации циклических вычислений необходимо рассчитывать члены ряда, сравнивать их значения с заданной точностью |a_n|>E и при выполнении условия сравнения производить их суммирование. Цикл завершается, когда |a_n|  E.

Для организации циклического вычисления сначала запишем выражения для n-го и (n +1)-го членов ряда заданной функции:

Для расчета следующего a_n+1 члена ряда используем рекуррентное соотношение, связывающее его с предыдущим a_n членом через общий множитель q_n.

Тогда a_n+1 = a_n  q_n. Такой подход позволит избежать вычисление факториала и возведения в произвольную степень. Произведем алгебраические преобразования и упростим выражение для q_n.

П одставляя n=0 в заданную формулу , получим начальные значения для расчета функции e^-x . А именно: n=0, a₀=1, s₀= a₀.

На рис. 4.5 приведёна блок-схема, программа и результаты,

подтверждающие решение задачи.

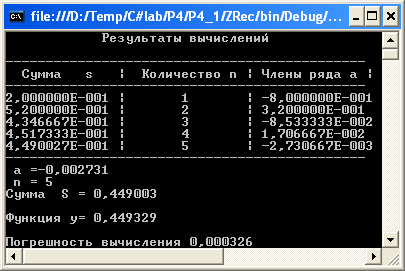
Как видно для представления функции e^-x c точностью вычисления E=0.001 при x=0.8 достаточно сложить первые 6 членов ряда (a₀,…a₅).

Измените, точность вычисления Е. Проанализируйте результат представления заданной функции. Сделайте выводы, как погрешность вычисления влияет на результат представления функции.