1.3.5. Визначення напору насоса при проектуванні

Формулами попереднього параграфа можна скористатися тільки для визначення напору і тиску насоса на діючій установці. Якщо насосна станція тільки проектується, то показання манометрів і вакууметрів нам не відомі і їх також треба визначити.

Примінимо рівняння Бернуллі для потоку реальної рідини на ділянці між перерізами 0-0 та 1-1 (див. мал. 3):

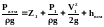, або:

( 3 )

Тут за площину порівняння прийнято площину 0-0, тиск на вільну поверхню прийнято Р_атм , повні втрати напору між перерізами 0-0 та 1-1 - h_всм . Швидкістю руху рідини в перерізі 0-0 нехтуємо (тобто вважаємо, що рівень рідини в резервуарі залишається незмінним).

Скориставшися рівнянням Бернуллі для потоку рідини між перерізами 2-2 та 3-3 ( див. мал. 3), отримаємо:

, ( 4 )

де: Z₃ = Н_г - геодезична (геометрична) висота підйому води; h_нап - повні втрати напору в напірному трубопроводі. Решта позначень попередня.

Підставивши вирази ( 3 ) та ( 4 ) в формулу ( 1 ), отримаємо:

Н = Н_г + h_нап + h_всм . ( 5 )

Таким чином, напір насоса дорівнює сумі геометричної висоти підйому рідини (статичний напір) і повних втрат напору, що виникають при русі рідини по усмоктувальному та напірному трубопроводах.

При проектуванні геометрична висота підйому завжди відома. Вона дорівнює різниці відміток рівней води в напірному та усмоктувальному резервуарах.

Повні втрати напору при русі рідини складаються із втрат напору на тертя по довжині труби та втрат напору в місцевих опорах.

Втрати напору по довжині можна обчислити по одній із формул гідравліки:

(формула Дарсі),

або: h_довж = SQ² = A₀kLQ² , де:

 - коефіцієнт тертя; L - довжина трубопроводу; V- швидкість руху рідини; d - діаметр трубопроводу; g - прискорення сили тяжіння; S - коефіцієнт опору трубопроводу; Q -витрата по трубопроводу; А₀ - коефіцієнт питомого опору трубопроводу; k - коефіцієнт, який коригує неквадратичність залежності.

В практиці розрахунків систем водопостачання широкого поширення набула формула:

h_довж = і L ,

де: і - гідравлічний ухил.

При розрахунках за останньою формулою необхідно користуватися спеціальними таблицями (наприклад [17]).

Втрати напору в місцевих опорах найчастіше обчислюють по формулі Вейсбаха:

де:

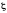- коефіцієнт місцевого опору.

При проектуванні насосних станцій в напірних трубопроводах за межами станції обчислюють втрати напору тільки по довжині. Втрати напору в місцевих опорах цих трубопроводів приймаються без розрахунку в розмірі 10-20 від втрат напору по довжині.

Втрати напору в усмоктувальних трубопроводах насосних станцій обчислюються за наведеними вище формулами. При цьому значення коефіцієнтів місцевих опорів беруть із справочної літератури (наприклад [ 9 ], або додаток 1 ).

Втрати напору в комунікаціях самої насосної станції (включаючи камеру переключень) найчастіше приймають без розрахунку в розмірі 2-4 метри водяного стовпа.

1.3.6. Рух рідини в робочому колесі відцентрового насоса

Робоче колесо відцентрового насоса є його основним робочим органом, тому кінематичні характеристики рідини, яка рухається через робоче колесо, вирішальним чином впливають на енергетичні параметри насоса.

Малюнок 4.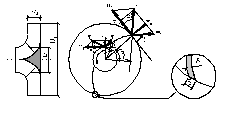

Рідина всередині міжлопасного каналу робочого колеса обертається разом з робочим колесом (тобто здійснює переносний рух). Окрім того, вона ще переміщується і відносно робочого колеса рухаючись від центра колеса до його периферії (при цьому рідина здійснює відносний рух). У відповідності з цим розрізняють такі види швидкостей руху частинок рідини в робочому колесі відцентрового насоса:

1 - швидкість переносного руху (окільна швидкість). Її позначають буквою ;

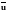2 - швидкість відносного руху. Позначається ;

3 - швидкість абсолютного руху , яка є сумою векторів переносної та відносної швидкостей .

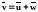В основу теоретичного уявлення про сталий рух потоку рідини через робоче колесо відцентрового насоса покладено гіпотезу про цівочний рух. Згідно цій гіпотезі, кожна частинка рідини всередині міжлопасного каналу рухається по траекторії форма якої співпадає з кривою обрису лопатки. Точно кажучи, такий рух можливий тільки в тому випадку, коли міжлопасні канали будуть безкінечно тонкими, що відповідає наявності безкінечно великої кількості безкінечно тонких лопаток. Зрозуміло, що практично це нездійсненно. Але, якщо міжлопасні канали мають велику довжину в порівнянні з їх поперечними розмірами, то, в цілому, траекторія руху частинок рідини в таких каналах буде приблизно відповідати формі цих каналів (тобто формі лопаток). Це і є практичною підставою для прийняття гіпотези про цівочний рух.

Швидкість переносного руху завжди направлена по дотичній до кола по якому обертається точка. Напрямок цієї швидкості співпадає з напрямком обертання. Для частинки рідини, що знаходиться в міжлопасному каналі на відстані r від центру обертання, величина переносної (окільної) швидкості визначається формулою: , де:  - кутова швидкість колеса; n - кількість обертів колеса за хвилину.

Як видно з цієї формули, окільна швидкість руху частинки рідини буде зростати по мірі її переміщення від центру до периферії робочого колеса ( тобто по мірі збільшення r). При вході в робоче колесо ця швидкість дорівнює , а при виході , де r₁ і r₂ - радіуси робочого колеса, відповідно, на вході та на виході рідини.

Якщо прийнято гіпотезу про цівочний рух, то відносна швидкість руху рідини завжди буде направлена по дотичній до поверхні лопатки в сторону виходу із робочого колеса. Величина цієї швидкості буде зменшуватися по мірі переміщення частинки рідини від центру до периферії робочого колеса. Це пояснюється збільшенням поперечного перерізу міжлопасних каналів.

Абсолютна швидкість руху частинки рідини визначається як сума двох векторів і за правилом паралелограма.

 - кут між напрямками абсолютної та переносної швидкостей.

 - робочий кут лопатки. Це кут між вектором відносної швидкості та напрямком, протилежним переносній швидкості.

V_r - проекція абсолютної швидкості на напрямок радіусу: V_r = V sin  .

V_u - проекція абсолютної швидкості на напрямок окільної швидкості: V_u = V cos  .

Як видно із паралелограма швидкостей (малюнок 4), проекція відносної швидкості на напрямок радіусу W_r дорівнює відповідній проекції абсолютної швидкості:

W_r = V_r = V sin  .