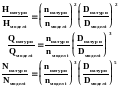1.3.17. Подібність насосів. Формули перерахунку.

Складний характер руху реальної рідини в робочих органах лопасних насосів призводить до того, що виключно теоретично розрахувати усі елементи насоса неможливо.Тому при проектуванні нових конструкцій насосів користуються експериментальними даними, які отримані при есплуатації подібних насосів на діючих станціях, або при випробуваннях моделей насосів в лабораторних умовах.

Для того, щоб результати досліджень, проведених на моделях , можна було застосовувати при розрахунку реальних насосів необхідно дотримуватися вимог теорії про механічну подібність руху реальної рідини. Ці вимоги полягають у необхідності дотримання умов геометричної, кінематичної і динамічної подібності. У випадку моделювання лопасних насосів ці умови можна означити так.

Геометрична подібність вимагає, щоб усі лінійні розміри одного з насосів (модель) були в однакову кількість разів менше (або більше) відповідних розмірів іншого насоса (натурного). Математично ці умови можна записати у вигляді постійності лінійного коефіцієнта подібності (маштабу моделювання):

Звідси витікає, також, постійність співвідношення будь яких розмірів у моделі і натури:

При суворому дотриманні геометричної подібності необхідно також дотримуватись подібності усіх виступів шершавості та зазорів. Однак ця вимога може бути виконана далеко не завжди. Наприклад, при масштабі моделювання 20, виступи шершавості висотою 1мм реального насоса, на моделі повинні мати висоту 0,05мм. Досить точно відтворити форму виступів при цьому неможливо.

Кінематична подібність вимагає, щоб співвідношення швидкостей усіх частинок рідини у моделі і у натурного насоса були рівними, а траєкторії їх руху були геометрично подібними. Математично ці умови можна записати у вигляді постійності ряду співвідношень:

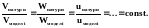
Необхідно, також, витримувати постійність співвідношення швидкості протікання рідини до швидкості руху деталей насоса.

При дотриманні геометричної подібності можна одержати ще одну умову кінематичної подібності:

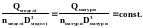
Ця умова має важливе значення при моделюванні насосів.

Динамічна подібність окрім геометричної та кінематичної подібності вимагає ще і пропорційності усіх сил, які діють у відповідних точках потоку ( сили тиску, ваги, інерції, в’язкості). В загальному виді динамічна подібність обумовлюється рівністю чисел Ейлера , Фруда 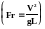, Рейнольдса , Струхаля 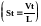для моделі і для натурного потоку.

При вирішенні задач гідромеханіки часто користуються не усіма критеріями одночасно, а тільки окремими із них. Вибір цих критеріїв залежить від характеру сил, що переважають у потоці, який моделюється. Так числом Ейлера користуються при моделюванні сил тиску, числом Рейнольдса - сил в’язкості, числом Фруда - сили ваги а числом Струхаля - сил інерції.

При моделюванні насосів важливе значення має критерій Ейлера. Стосовно до цього випадку критерій подібності Ейлера можна привести до такого виду: .

Але швидкість V пропорційна відношенню Q / D² , тоді ,

а умову подібності можна записати так:

Це рівняння установлює залежність між головними енергетичними параметрами (подача і напір) модельного і натурного насосів.

Для перерахунку результатів, які отримані на моделі, у параметри натурного насоса користуються формулами перерахунку.

Припустимо, що геометрично і кінематично подібні одно до одного робочі колеса однотипних насосів діаметрами D_моделі і D_натури обертаються з частотами n_моделі і n_натури , створюючи при цьому напори Н_моделі і Н_натури та подачі Q_моделы і Q_натури .

При умові радіального входу в робоче колесо із головного рівняння відцентрового насоса маємо:

,

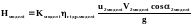. Тоді:

Із умови геометричної подібності витікає, що К_натури = К_моделі . Із кінематичної подібності - _{2натури} = _{2моделі} . Маючи на увазі, що швидкість u₂ пропорційна добутку nD₂ , отримуємо:

Відношення подач двох насосів буде дорівнювати:

.

При геометрично і кінематично подібних колесах маємо _{2натури} = _{2моделі} ; _{2натури} = _{2моделі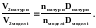} ; ; З урахуванням цих залежностей:

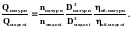
Потужність насоса змінюється пропорційно добутку QH, або:

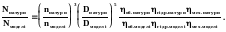
Формули співвідношень подач, напорів та потужностей насосів, які отримано на підставі подібності лопасних насосів, називають формулами перерахунку. Вони дають можливість розрахувати головні параметри насоса, який проектується, якщо відомі параметри насоса геометрично і кінематично йому подібного.

Крім того, формули перерахунку дають можливість визначити параметри насоса при різних частотах обертання, випробувавши насос при одній частоті.

Для приблизних розрахунків величини коефіцієнтів корисної дії модельного і натурного насосів можна прийняти рівними. При цьому формули перерахунку значно спрощуються: