§ 5. Интегрирование тригонометрических функций
Договоримся
всюду в дальнейшем символом
обозначать любую рациональную функцию
от 2-х аргументов
и
.
Покажем
интегрируемость в элементарных функциях
любой функции вида
Сделаем замену:
;
.
Таким образом,
- интеграл от рациональной дроби, т.к.
рациональная функция от рациональных
функций также представляет собой
рациональную функцию.
Подстановка называется универсальной тригонометрической подстановкой.
Пример 49.
.
Используем универсальную тригонометрическую постановку:
где
.
В силу непрерывности первообразной
имеем:
т.е.
,
откуда следует, что
,
поэтому
.
Осталось установить связь между
и
:
из неравенства
получим, что
,
а, значит,
.
Таким образом,
Универсальная тригонометрическая подстановка часто приводит к громоздким выкладкам. Укажем ряд частных случаев, когда интеграл может быть рационализирован с помощью других, более простых подстановок.
Предварительно сделаем следующие замечания из области алгебры:
1. если
то
2. если же
то
что сразу вытекает из замечания 1, если
применить его к функции
:
т.е. для функции
справедливо замечание 1, а тогда
;
3. если
то
;
действительно,
введя обозначение
,
получим
- для функции
выполнено 1, т.е.
или
Вернёмся к
1. если
,
то согласно замечанию 2
и
2. если
то согласно замечанию 2
и
3. если
то согласно замечанию 3
и
.
Замечание.
Любую рациональную функцию
можно представить в виде суммы выражений,
рассмотренных выше типов:
,
здесь первое выражение меняет знак при
изменении знака
,
второе меняет знак при изменении знака
,
а последнее остаётся неизменным при
одновременном изменении знаков
и
.
Пример 50.
.
Пример 51.
.
Пример 52.
.
Иногда интегрирование тригонометрических функций может быть осуществлено непосредственно или с использованием метода интегрирования по частям, а также всевозможных тригонометрических формул, что иллюстрируют нижеследующие примеры.
Пример 53. Вывести формулы понижения для интегралов:
1)
;
2)
;
3)
;
4)
.
1)
.
Ко второму интегралу
справа применим формулу интегрирования
по частям:
,
,
,
,
поэтому
,
откуда следует:
.
2)
.
Используем интегрирование по частям к интегралу справа:
,
,
,
,
следовательно,
,
поэтому
.
3)
.
Интегрируем по частям интеграл в правой части:
,
,
,
,
.
4)
.
К интегралу
применим формулу
интегрирования по
частям:
,
,
,
,
поэтому
.
Пример 54.
.
Используя
формулы
,
,
и формулы понижения
степени
,
,
преобразуем подинтегральную функцию:
.
Тогда
Пример 55.
если
.
Следующие примеры показывают, что во многих случаях можно не только избежать универсальной тригонометрической подстановки, но и даже получить некоторые общие формулы.
Пример 56.
.
С помощью простейших преобразований
и с использованием примера 22, получим:
.
Пример 57.
,
где
и
.
Покажем, что в данном случае можно проинтегрировать, не прибегая к универсальной тригонометрической подстановке.
Для этого представим числитель данной дроби в виде линейной комбинации знаменателя и его производной:
.
Для нахождения
постоянных
приравниваем коэффициенты при
и
в правой и левой частях тождества:
,
.
Тогда
.
Пример 58.
.
Используя предыдущий пример, получим:
.
Пример 59. Доказать рекуррентную формулу:
,
где
,
,
,
и с её помощью найти интеграл
.
Воспользуемся интегрированием по частям:
,
откуда следует:
.
Тогда, используя
полученную формулу и пример 53, получим:
.
Рассмотрим
интегралы вида
,
.
Сделаем замену
,
,
,
,
тогда
− подинтегральное выражение представляет
собой биномиальный дифференциал, и,
следовательно (как будет рассмотрено
в следующем §), интегрируется в конечном
виде только в трёх случаях: 1)
;
2)
;
3)
или
1)
;
2)
;
3)
.
Если оба показателя степени
− целые, имеем рациональную функцию
- данная ситуация рассматривалась выше.
Пример 60.
.
Пример 61.
.
Сделаем замену
,
,
,
тогда
.
Раскладывая
полученную дробь на простые дроби, будем
иметь:
,
откуда следует алгебраическая система
для определения
:
решением
которой является
,
.
Интегрируя, получим:
.
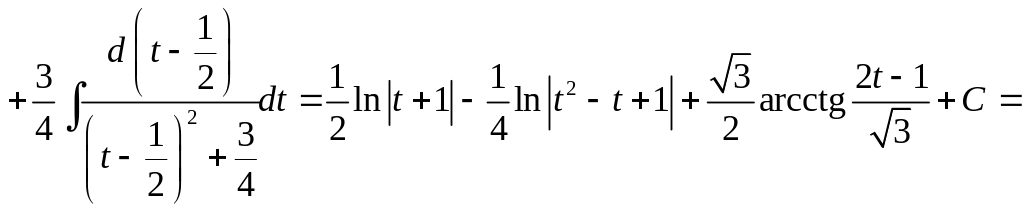