Метод Остроградского
Если знаменатель
правильной рациональной дроби
имеет комплексные кратные корни, то
разложение этой дроби на простые будет
содержать дроби IV
-го типа, интегрирование которых связано
с громоздкими выкладками. Для подобных
интегралов М.В.Остроградским был придуман
остроумный метод. Этот метод основан
на анализе интегралов от простых дробей
4-х типов. Интегралы от дробей I-го
и III
-го типов являются нерациональными
функциями. Интеграл от дроби II-го
типа является правильной рациональной
дробью со знаменателем, равным тому же
двучлену в степени на единицу меньшей.
Интеграл от дроби IV-го
типа равен сумме правильной рациональной
дроби со знаменателем, равным тому же
трёхчлену в степени на единицу меньшей,
и интеграла вида
,
приводящегося к арктангенсу. Тогда,
если знаменатель
правильной рациональной дроби имеет
вид:
то рациональная
часть интеграла
равна сумме правильных рациональных
дробей со знаменателями
,
,
...,
,
,
,
...,
,
т.е. она представляет собой правильную
рациональную дробь
,
где
Сумма дробей I-го
и III-го
типов, интегралы от которых представляют
собой нерациональные функции, будет
равна:
,
где
Таким образом,
мы приходим к тождеству, полученному
Остроградским:
+
.
Здесь
и
- многочлены с неопределёнными
коэффициентами, их степени естественно
задать на единицу меньше степеней
многочленов
и
соответственно. Для вычисления
неопределённых коэффициентов данное
тождество следует продифференцировать,
привести результат справа к общему
знаменателю и сопоставить коэффициенты
при одинаковых степенях
в числителях левой и правой частей.
Проиллюстрируем метод М.В.Остроградского примерами.
Пример 40.
.
Согласно методу Остроградского получим:
.
Дифференцируя данное тождество, будем иметь:
.
Приравнивая
коэффициенты при одинаковых степенях
в числителях, получим систему алгебраических
уравнений для определения значений
неизвестных
:
Из
и
следует, что
.
Из
:
;
из
и
имеем
;
из
и
следует, что
;
из
имеем:
;
поэтому из
получаем:
,
а, значит,
,
.
Таким образом, тожество принимает вид:
.
Под интегралом
справа имеем сумму простых дробей I–го
и III–го
типов:
.
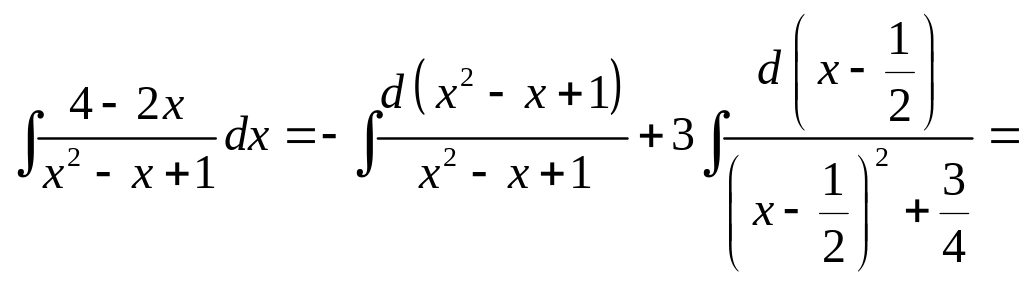
Итак, исходный интеграл равен:
=
.
Пример 41.
.
Применение метода Остроградского приводит нас к тождеству:
После
дифференцирования этого тождества
будем иметь:
.
Приводим справа к общему знаменателю и приравниваем
коэффициенты в числителях при одинаковых степенях :
;
Из 2-го и 7-го, 3-го
и 8-го, 4-го и 9-го, 5-го и 10-го уравнений
следует:
Из 6-го и последнего уравнений получим:
.
Итак, исходный интеграл принимает следующий вид:
.
Интеграл
легко
может быть найден с помощью элементарных
преобразований методом подведения под
знак дифференциала:
.
Следовательно,
Отметим, что при интегрировании рациональных дробей не всегда необходимо применять теорему о разложении правильной дроби на простые или метод М.В.Остроградского. Иногда с помощью элементарных преобразований, метода поведения под знак дифференциала или интегрирования по частям можно получить результат гораздо быстрее и проще. Продемонстрируем это.
Пример 42.
.
Пример 43.
.
Пример 44.
.
Пример 45.
.
Пример 46.
.
Сделав замену
,
получим разность интегралов
,
к которым легко может быть применена
теорема о разложении на простые дроби:
Таким образом,
.
Интегрируя, будем иметь:
ведь
.
Возвращаясь к переменной , получим ответ:
.
Пример 47.
Дифференцируя,
получим:
,
откуда следует:
Решение этой
системы:
Итак,
и, возвращаясь к переменной , окончательно получим:
.
Пример 48.
.
В следующих параграфах рассмотрим некоторые классы нерациональных функций, интегрируемых в элементарных функциях. Применяя соответствующую подстановку, мы будем сводить данный интеграл к интегралу от рациональной дроби.