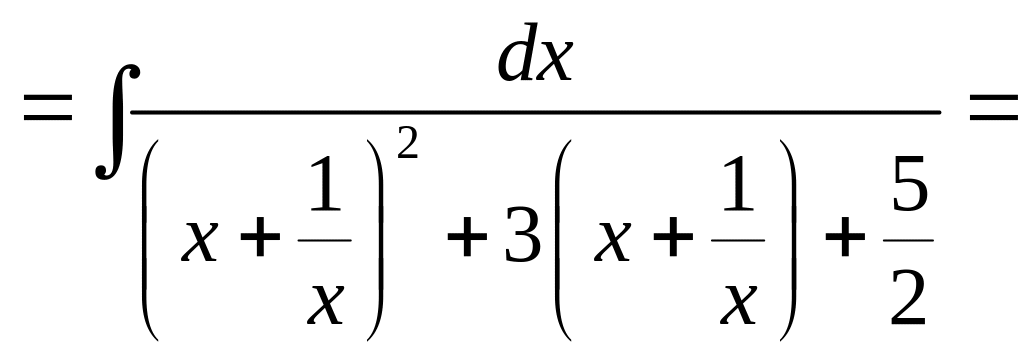§ 4. Интегрирование рациональных функций

Рассмотрим рациональную функцию , где , – многочлены с вещественными коэффициентами. Если степень многочлена больше степени многочлена , то такая дробь называется правильной рациональной дробью, в противном случае – неправильной. Если дробь - неправильная, то её можно представить в виде суммы многочлена и правильной дроби: , здесь степень многочлена меньше степени многочлена . Поэтому интегрирование неправильной рациональной дроби сводится к интегрированию многочлена и правильной дроби.

Определение. Рациональные дроби вида , , где , , , называются элементарными или простыми дробями.

Теорема (основная). Пусть – правильная рациональная дробь, знаменатель которой имеет вид:

. Тогда для этой дроби справедливо следующее разложение (тождество):

, где – некоторые вещественные постоянные.

Таким образом, теорема утверждает, что всякая правильная рациональная дробь может быть разложена на сумму простых дробей. Для получения конкретного разложения правильной дроби нужно в правой части тождества привести дроби к общему знаменателю и после этого приравнять коэффициенты при одинаковых степенях в числителях правой и левой частей.

Отметим, что иногда разложение дроби на сумму элементарных может быть получено путём простейших преобразований. Например,

.

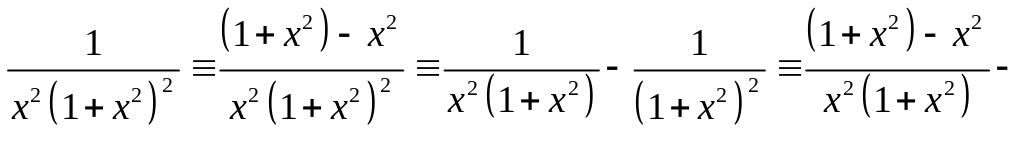
Проинтегрируем элементарные дроби. Их можно разделить на 4 типа.

I.

II.

III. где , , поэтому

;

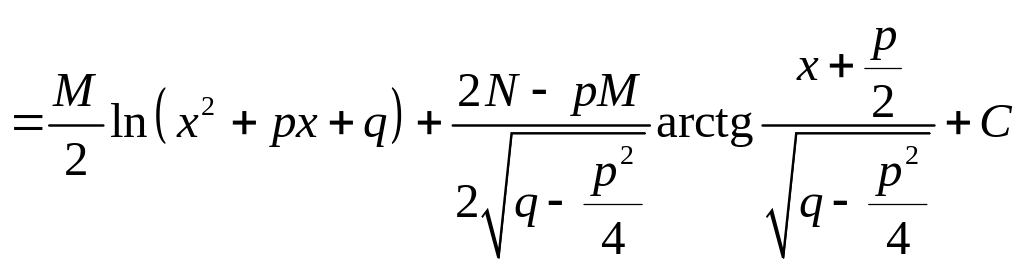IV. применяя тот же приём, что и в случае III, имеем:

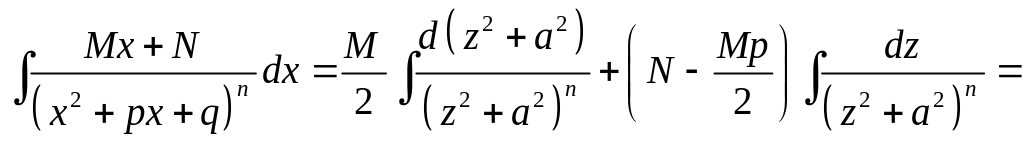
, а для интеграла воспользуемся рекуррентной формулой из примера 35. Возвращаясь к переменной , получим окончательный результат.

Итак, интегралы от простых дробей представляют собой элементарные функции, ибо выражаются через логарифмы, арктангенсы и рациональные функции. Тем самым мы приходим к теореме, исчерпывающей проблему интегрирования рациональной дроби.

Теорема. Всякая рациональная дробь интегрируется в элементарных функциях.

Отметим, что главной трудностью при интегрировании рациональных дробей является разложение многочлена на произведение неприводимых сомножителей, т.е. отыскание вещественных и комплексных корней многочлена .

Пример 36. .

Так как под интегралом имеем правильную дробь, то согласно теореме она разлагается на простые дроби следующим образом:

, откуда следует тождество:

.

В данном случае мы можем обойтись без приравнивания коэффициентов при одинаковых степенях , а воспользоваться тем, что знаменатель исходной дроби имеет лишь вещественные корни. Полагая в последовательно и , получим систему уравнений для определения и :

Следовательно,

.

Пример 37. .

Разложение данной правильной дроби на элементарные имеет следующий вид:

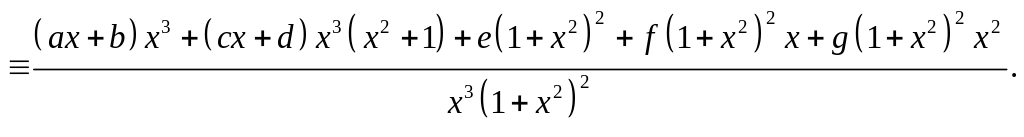
Приравниваем коэффициенты при одинаковых степенях в числителях правой и левой частей тождества:

Из следует, что , а из – , а тогда из получим ; из – , а из будем иметь: .

Итак,

.

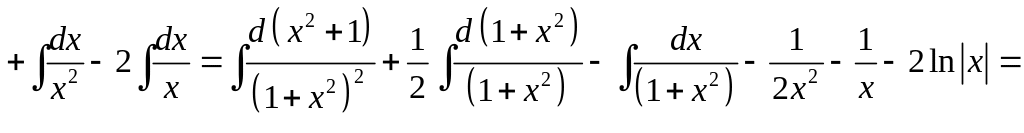
Пример 38. .

,

, откуда следует система уравнений: 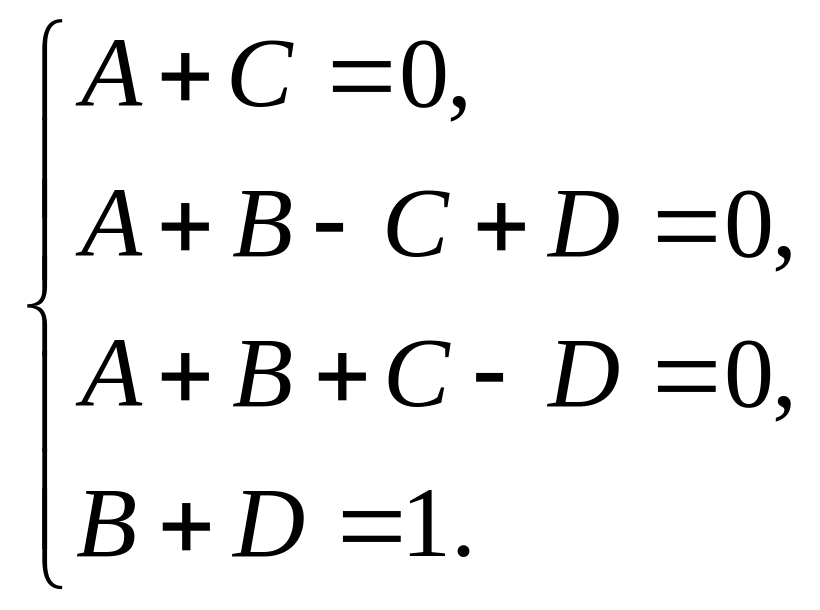Её решение: .

Тогда = =

.

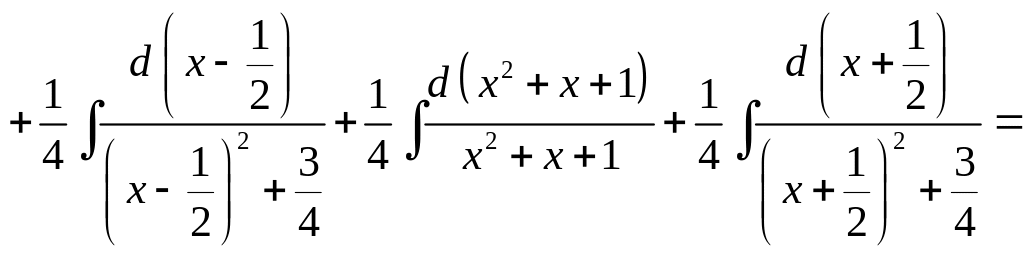
Пример 39. =
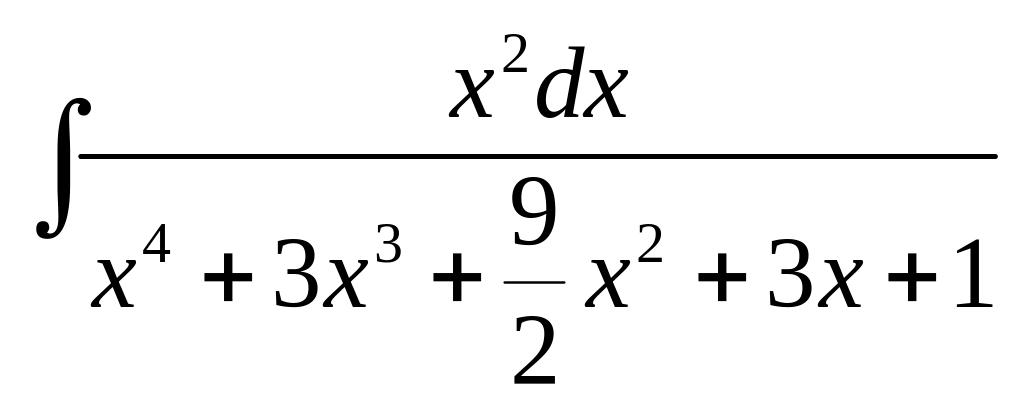
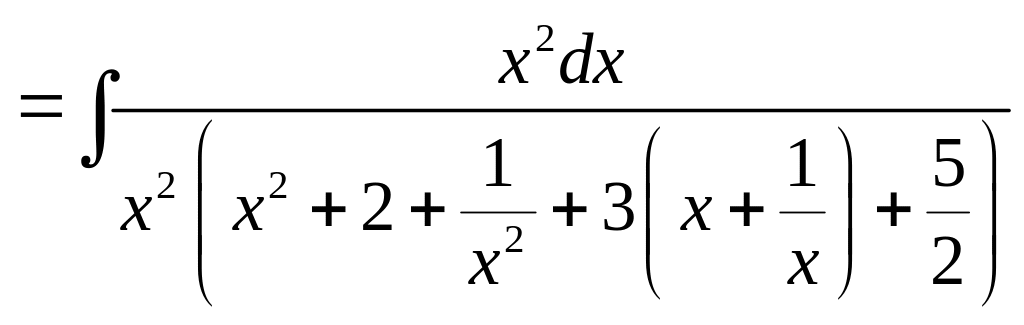