1.14. Требования к линиям электропередач

Одним из важнейших требований к линиям электропередач (ЛЭП) является уменьшение потерь при доставке энергии потребителю. Эти потери в настоящее время заключаются в нагреве проводов, то есть переходе энергии тока в тепловую энергию, за что ответственно омическое сопротивление проводов. Иными словами задача состоит в том, чтобы довести до потребителя как можно более значительную часть мощности источника тока 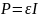при минимальных потерях мощности в линии передачи , где , причём на этот раз есть суммарное сопротивление проводов и внутреннего сопротивления генератора, (последнее всё же меньше сопротивления линии передач).

В таком случае потери мощности будут определяться выражением:

.

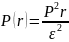Отсюда следует, что при постоянной передаваемой мощности её потери растут прямо пропорционально длине ЛЭП и обратно пропорционально квадрату ЭДС. Таким образом, желательно всемерное её увеличение, что ограничивается электрической прочностью обмотки генератора. И повышать напряжение на входе линии следует уже после выхода тока из генератора, что для постоянного тока является проблемой. Однако, для переменного тока эта задача много проще решается с помощью использования трансформаторов, что и предопределило повсеместное распространение ЛЭП на переменном токе. Однако при повышении напряжения в ней возникают потери на коронирование и возникают трудности с обеспечением надёжности изоляции от земной поверхности. Поэтому, наибольшее, практически используемое, напряжение в дальних ЛЭП не превышает миллиона вольт.

Кроме того, любой проводник, как показал Максвелл, при изменении силы тока в нём, излучает энергию в окружающее пространство, и потому ЛЭП ведёт себя как антенна, что заставляет в ряде случаев наряду с омическими потерями брать в расчёт и потери на излучение.

2. Теория лабораторной работы

На рис. 16 представлена цепь постоянного тока, где – внутреннее сопротивление источника тока, – электродвижущая сила, а R – сопротивление нагрузки.

Полная электрическая мощность, выделяемая в цепи, слагается из мощностей, выделяемых во внешней и во внутренней частях цепи:

.

Так как , то:

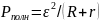. (14)

Эта мощность выделяется за счет работы сторонних сил источника тока.

По закону Ома сила тока в цепи: 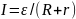и достигает максимального значения при (ток короткого замыкания):

.

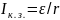С ростом , сила тока стремится к нулю. Наибольшего значения мощность достигает при токе короткого замыкания.

М

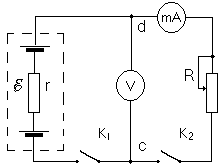
Рис. 16.

ощность во внешней цепи (полезная мощность) равна:

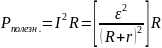. (15).

Наибольшего значения 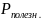достигает при .

В этом случае:

.

Коэффициент полезного действия:

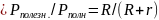. (16)

При неограниченном возрастании , коэффициент полезного действия стремится к 1.

Измерения и обработка результатов

1. Ознакомиться с работой схемы (рис.16).

2. Замкнуть ключ ( 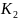– разомкнут).

Строго говоря, вольтметр покажет разность потенциалов между точками с и d:

,

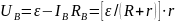где 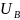– показания вольтметра, соответственно ток через вольтметр и его сопротивление. Однако, при большом , показания вольтметра будут мало отличаться от , т.е. приблизительно равно : .

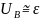3. Установить на магазине сопротивлений и замкнуть . Амперметр покажет ток короткого замыкания 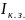. Зная , вычислить внутреннее сопротивление источника тока:

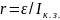
4. Изменяя сопротивление нагрузки (см. п. 5), значения тока и напряжения занести в таблицу 1 (не менее 20 - 24 измерений).

Таблица 1.

= _______, В; = _______, А; = _______, Ом.
№ измерения
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

5. С целью получения точных результатов рекомендуется изменять значение на магазине со следующим шагом :

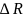В диапазоне от 0 до 2 сопротивление на магазине следует изменять с шагом 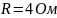. В интервале близком к изменение . В интервале 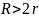изменение .

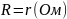6. Обесточить установку.

7. По результатам измерения , , вычислить по формулам (14), (15), (16) значения 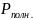и .

8. П

   

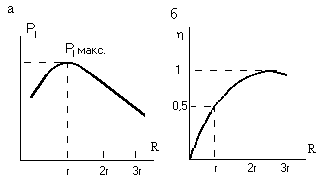
   Рис.17.

   остроить зависимост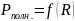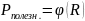и , и , откладывая значения по оси абсцисс (рис.17).

9. Произвести соответствующие расчёты по формулам и экспериментальное определение искомых величин по графику (табл. 2).

Таблица 2

Расчёт по формулам			Эксперимент (по графику)
	,	А		,	А
	,	В		,	В
	,	Вт		,	Вт
=	,	Вт		,	Вт
=	,	%		,	%

10. Проанализировать результаты, сделать вывод.
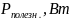
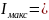
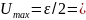
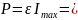
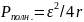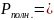
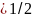