КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ФИЗИЧЕСКИЙ ФАКУЛЬТЕТ

ЛАБОРАТОРНЫЙ ПРАКТИКУМ

ПО КУРСУ

Магнитная радиоспектроскопия

(ЧАСТЬ ВТОРАЯ)

ЛАБОРАТОРНАЯ РАБОТА

ИМПУЛЬСНЫЙ ЯДЕРНЫЙ МАГНИТНЫЙ РЕЗОНАНС

В ТВЁРДЫХ ТЕЛАХ

КАЗАНЬ 2004

Печатается по решению Редакционно-издательского совета физического факультета

УДК 537.635; 537.611.43

Лабораторный практикум по курсу “Магнитная радиоспектроскопия”

(часть вторая)

Аннотация

В методическом пособии к лабораторной работе “Импульсный ядерный магнитный резонанс в твёрдых телах” для студентов четвёртого курса изложены основы теории импульсного ЯМР и ядерной магнитной релаксации в диамагнитных диэлектрических кристаллах в классическом и квантово-механическом рассмотрении, приведена методика измерения времён релаксации. В пособии также дано краткое описание устройства и принципа работы лабораторной установки.

Составители: Егоров А.В.,

Дуглав А.В.,

Кудряшов А.А.

Рецензент: зав. кафедрой молекулярной физики КГУ, док. ф.– м. н.,

проф. Скирда В.Д.

 Физический факультет Казанского государственного университета, 2004.

С О Д Е Р Ж А Н И Е

Стр.

1. КЛАССИЧЕСКОЕ РАССМОТРЕНИЕ ИМПУЛЬСНОГО ЯМР……………....4

1.1. Движение невзаимодействующих спинов……………………………..4

1.2. Вращающаяся система координат (ВСК)……………………………....4

1.3. Сигнал спиновой индукции (ССИ)……………………………………..7

1.4. Спиновое эхо……………………………………………………………..9

2. КВАНТОВОМЕХАНИЧЕСКОЕ РАССМОТРЕНИЕ

Импульсного ямр…………………………………………………….…..10

2.1. Уравнение движения……………………………………………………10

2.2. Статистический ансамбль невзаимодействующих спинов…………..11

2.3. Спад спиновой индукции и спиновое эхо………………………....….13

3. ЯДЕРНАЯ СПИН–РЕШЁТОЧНАЯ РЕЛАКСАЦИЯ………………………….14

3.1. Модель случайного поля……………………………………………….15

3.2. Влияние ядерной спиновой диффузии на ядерную релаксацию

через парамагнитные центры……………………………………….…18

3.3. Ядерная релаксация через ПЦ в отсутствие ядерной спиновой диффузии………………………………………………………………..23

4. МЕТОДЫ ИЗМЕРЕНИЯ ВРЕМЁН РЕЛАКСАЦИИ………………………….26

5. ИМПУЛЬСНЫЙ СПЕКТРОМЕТР ЯМР……………………………………….28

5.1. Назначение………………………………………………………………28

5.2. Технические характеристики…………………………………………..28

5.3. Конструкция датчика…………………………………………………...29

5.4. Принцип действия………………………………………………………30

З а д а н и е ………………………………………………………………………....32

Л и т е р а т у р а …………………………………………………………………...32

1. Классическое рассмотрение импульсного ямр

1. Движение невзаимодействующих спинов

М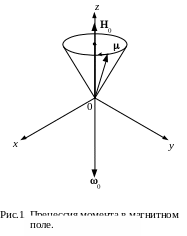 еханический ( ) и магнитный ( ) моменты ядер связаны следующим соотношением , где  – скалярная величина, называющаяся гиромагнитным отношением. Взаимодействие магнитного момента с постоянным магнитным полем вызывает прецессию механического момента. Уравнение движения магнитного момента может быть записано как

,

или, наконец, .

Угловая скорость (частота прецессии ) получила название ларморовской.

Если магнитное поле направлено вдоль оси z, то прецессия будет происходить так, как указано на рис.1, в направлении стрелки, с ларморовской частотой; магнитный момент описывает конус.

Приведённое уравнение движения записано в неподвижной системе координат, которую также называют лабораторной (ЛСК).

1.2. Вращающаяся система координат (вск)

При рассмотрении магнитного резонанса удобно использовать вращающуюся систему координат (ВСК). Последняя обладает некоторой угловой скоростью относительно лабораторной. Очевидно, что если ВСК вращается со скоростью ларморовской прецессии, то магнитный момент в этой системе координат будет неподвижен. Покажем это. Рассмотрим некоторую векторную функцию времени , где i, j, k – единичные векторы, направленные вдоль осей прямоугольной системы координат, вращающейся с угловой скоростью . Тогда для этих векторов справедливы следующие уравнения:

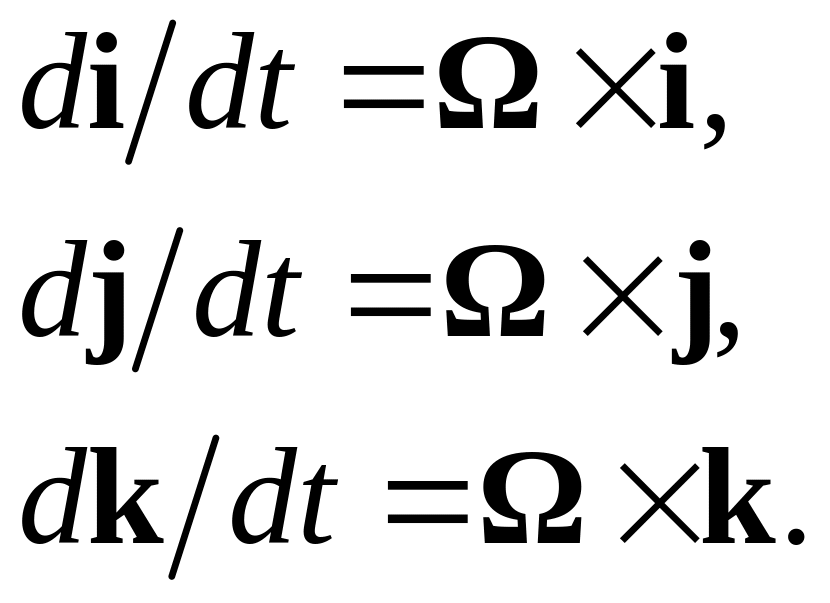
Полная производная функции F по времени равна

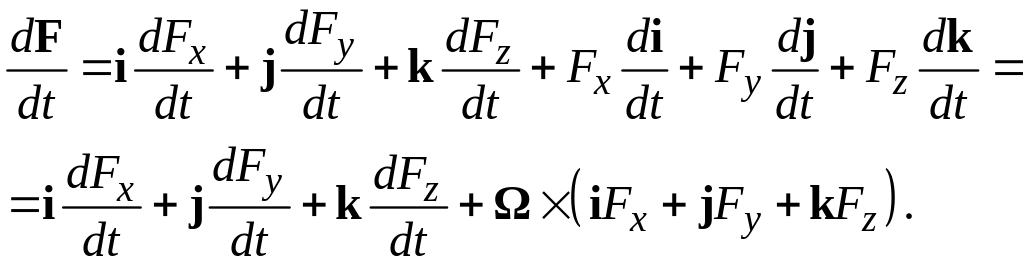
Первые три слагаемых представляют собой не что иное, как производную функции в ВСК. Обозначим её как . Тогда .

Таким образом, уравнение движения магнитного момента в системе координат, вращающейся с частотой , записывается как

(здесь и в дальнейшем мы будем пользоваться обычным обозначением производной векторной величины, оговаривая при этом какая система координат используется). Действительно, если , то , и прецессия отсутствует. Можно представить себе, что в ВСК прецессия обусловлена эффективным магнитным полем, , где , а отсутствие прецессии есть следствие равенства нулю эффективного поля.

В макроскопическом объекте спины прецессируют с произвольной фазой, вследствие чего полный момент направлен параллельно магнитному полю , как показано на рис.2, а уравнение его движения в ВСК имеет такой же вид как для индивидуального момента – спина:

Допустим, что кроме поля имеется поперечное поле , направленное вдоль оси x ВСК. Это означает, что в ЛСК оно вращается с частотой в направлении прецессии. В этом случае эффективное поле , вокруг которого происходит прецессия намагниченности (рис.3), не обращается в нуль даже в случае, когда , и, следовательно, можно создать поперечную намагниченность, воздействуя относительно слабым переменным магнитным полем на частоте близкой к ларморовской. Это и называется магнитным резонансом. На практике для наблюдения ЯМР чаще всего используется одна катушка индуктивности. При протекании через неё переменного тока возникает линейно поляризованное переменное магнитное поле, направленное вдоль оси катушки, .

Т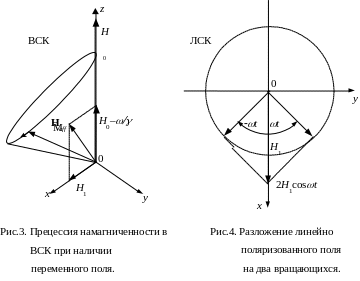 ем не менее, все соображения, приведённые выше, остаются в силе, поскольку его можно представить в виде суммы двух вращающихся с частотой  в противоположных направлениях полей величиной H₁, как показано на рис.4.

Составляющей, которая вращается в направлении противоположном направлению прецессии (справа на рисунке 4) можно пренебречь. Действительно, если и , то эффективное поле в этом случае составляет , и переменная составляющая не будет оказывать влияния на намагниченность.