5.2 Типтік тапсырманы шешу мысалы
Тапсырма: Екі айналу беттердің қиылысу түзуін құрастыру: конустық (Φ1) және сфералар (Φ2). 110 - суретте тапсырманың графикалық безендірілуі келтірілген.
Тапсырманың келісім бойынша символдармен жазылуы: Φ1, Φ2; Φ1 ∩ Φ2 = ℓ ?
Тапсырманың шешімі және анализі:
1) екінші реттегі айналым беттері қиылысады, соған байланысты ℓ түзудің қиылысуы төртінші реттегі қисығы болып табылады;
2) қиылысу түрі - «ойық» болғанмен (байланыспаған қиылыс), онда бір түзу ℓ түзумен қиылысады;
3) жалпы жазықтық беттері α1 симметриясына ие болады, фротальді жазықтық проекциясына параллель, олардың фронтальді қиылысу очерктер Φ1 және Φ2 бізге екі қос нүктелердің 1" – жоғарғы және 1* - төменгі сипатын береді;
4) арашашы ретінде келесі кезекпен құру, осы тапсырманы мақсатқа лайықты көлденең жазықтық а2 және а3 қабылдау және т.б., олардың қиылысу түзулері әрбір беттің қарапайымы (шеңберлі) болып табылады;
5) іздеген қисық ℓ көру шекара аймағы көлденең жазық проекциясына экватор сферасы болып табылады, сондықтан жазықтық - α2 арашашы Ф2 экватор сферасы өткізу арқылы бізге екінші қадам алгоритмі 2 және 2 экватор нүктесіне жататын сол жағы болып табылады;
6) Фронтальды жазықтық проекциясына көру шекарасы басты фронтальді меридиандар және 1-1* нүктелердің жататындығы болып табылады;
Осылайша, түзулердің құруы беттердің қиылысу мынаған келеді:
Біріншіден, α1 жазықтықты өткіземіз, фронтальді жазық проекциясына параллель болатын ось і және ј беттер арқылы өткіземіз. Көлденең жазық проекциясына – α1H = α1' бұл проекцияның ізі, Х осіне параллельді. Фронтальды прекциясында 1"-1*" нүктелерді және Φ1" и Φ2" очерк қиылысуын табамыз. Алған нүктелерді көлденең α1H = α1' проекцияның-ізі α1 жазықтықта көру есеппен сындырамыз (нүкте 1' – көрінетін, 1*' – көрінбейтін).
Алгоритмнің бірінші жазу қадамы түрінде:
1) α1║V;
α1
i,
Ј; α1
∩
Φ1
= m1;
α1
∩
Φ2
=
n1;
m1
∩
n1
= 1, 1*;
нүкте 1 – жоғарғы, нүкте 1* - төменгі.
Алгоритм кеңістік үшін жазылатының белгілейік, ал нүкте проекциясын құрастырғанда және ℓ түзуін әр жазық проекциясына құрылған барлық элементтерді міндетті түрде белгіленген түрде шығарылады.
Екіншіден, Φ2 экватор сфера арқылы α2 арашаш – жазықтықтың параллель көлденең жазық проекциясынан (көр.α2 V = α2") өткізу. m2 және n2 фронтальді проекция параллельдерді айырылмастай болғандықтан, m2" и n2" проекциялар бір-біріне жарым-жартылай жатқызылады. Сондықтан олардың m2' және n2' проекциясын құрастырамыз, шеңберлі радиусына сай және олардың 2' және 2*' қиылысу нүктедлер. 2" және 2*" Фронтальды проекция нүктелерін α2 V = α2" проекция-ізінде α2 жазықтығында байланыс проекция түзулерінде табамыз. Алгоритмнің екінші жазу қадамы түрінде:
2) α1║H; α2 ∩ Φ1 = m2; α2 ∩ Φ2 = n2; m2 ∩ n2 = 2, 2*;
нүкте 2 – сол жақ таяу, нүкте 2* - сол жақ адыс. Екі нүктенің – көру шекарасы.
Үшіншіден, α3, еркін жазықты өткіземіз, Н жазықтыққа параллель. Екінші қадамға m3' және n3' көлденең жазығын осы жазықтықта қиылысу түзулері әр бетінде және көлденең проекциясын 3' и 3*' , нүктесін 3 и 3. * табамыз, содан кейін алгоритмнің үшінші қадамына келесіні жазамыз:
3) еркін нүктелер α3 ǁ H; α3 ∩ Φ1 = m3; α3 ∩ Φ2 = n3; m3 ∩ n3 = 3,3*. Үйлестік түрінде 4, 5 нөмірі бар нүктелерді алуға болады және т.б., бірақ осы тапсырмада ондай қажеттілігі жоқ, өйткені сипаттама және қисық форма толық түрінде анықталған.
Төртіншіден, алған нүктелерді бір-бірімен қосамыз. Қаншалықты іздеген қисық ℓ тұйықталған болып табылады, оның құрастыруын кез-келген нүктеден және кез-келген бағытымен құрастыруға болады, мысалы, 1, 2, 3, 1*, 3*, 2*, 1. Қорытынды кезең алгоритмы мынан түрде жазылуы мүмкін:
ℓ = 1,2,3, 1*, 3*, 2*,1 және ℓ = 1*, 3*, 2*,1 .
Қиылысу түзулер бетінде жалпы алгоритмі бойынша әрдайым анықталмайды. Кейбір жағдайларда түзу формасын қиылысу бетінде құру көмекшісіз анықтауға болады. Осындай қиылыстардың мысалы біліктес қиылысу бетінде (беттер, жалпы айналу осьне ие болатындар) және қиылысу бетінде, Монжа әрекет теоремасына (бетінде, жалпы сфера айналына енгізген және жазылған) жататындар жатады.
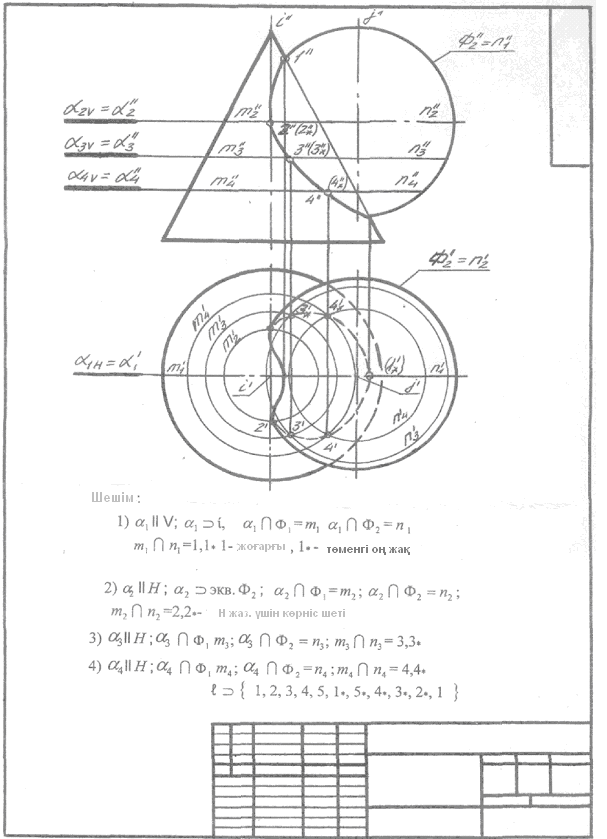
Сурет 110