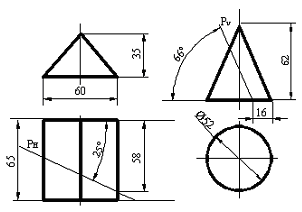
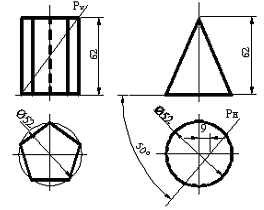
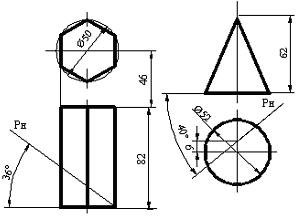
4.5.2 «Қима бетінің жазықтығының жеке орналасуы. Қашау бетінің салынуы»

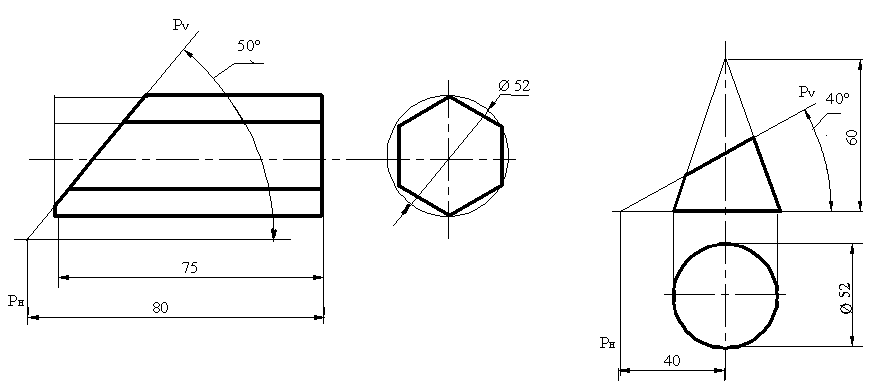
Сурет 104 Сурет 105

Алдын ала негізгі жағына тең (енінің шегі) алты бөлік қалдыратын түзуді өткізеді, бөліктің өлшемі профильдік проекциядан алынады. Сосын алынған нүктелерден түзу сызық өткізеді және фронтальді немесе көлденең проекцияда өлшенетін таңдалған қабырғалардың ұзындығына сәйкес қалдырылады. Тізілген нүктелерді бөлшектеп қосу және сынық сызық кескінін алу, негізгілерді реттейді және таңдалған бөлікті айналдырады.

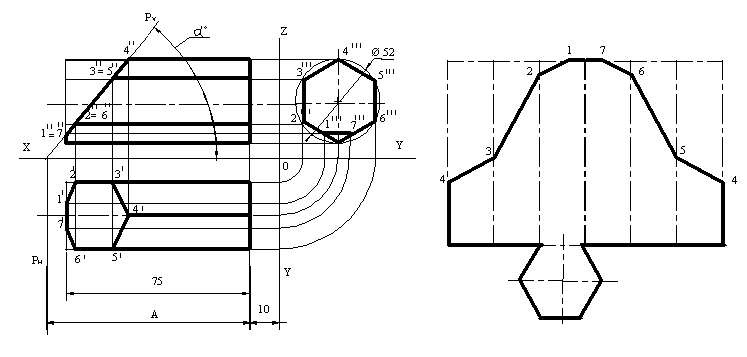
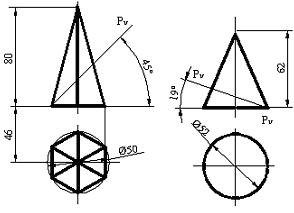
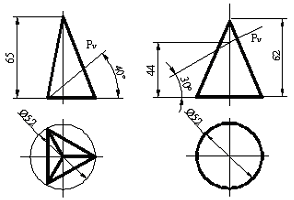
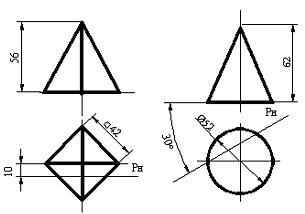
Сурет 106 Сурет 107

Төменде тапсырманың шешімі мысал ретінде П фронтальді-проекциялық жазықтығының конус айналу бетінің қиылысуымен кезекпе-кезек белгілеумен келтіріледі.

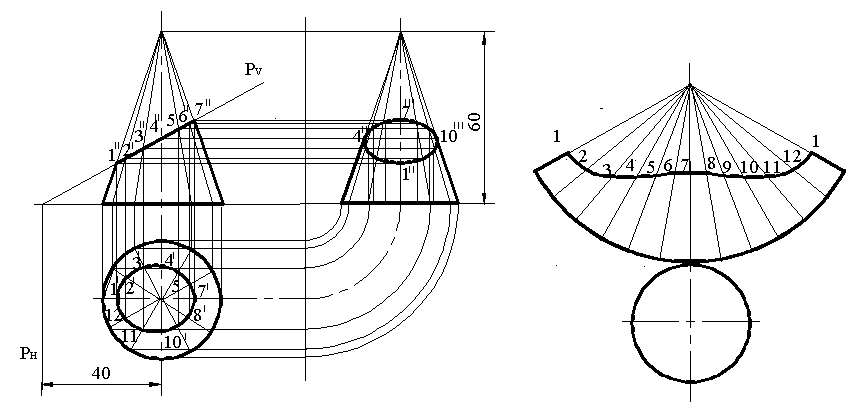
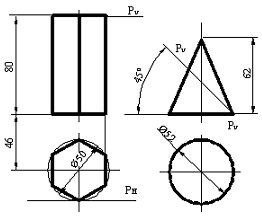
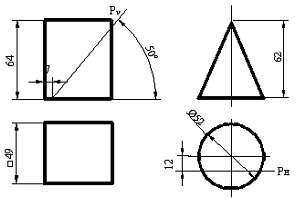
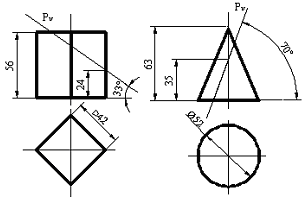
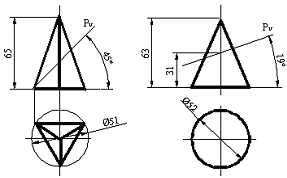
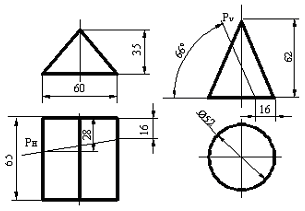
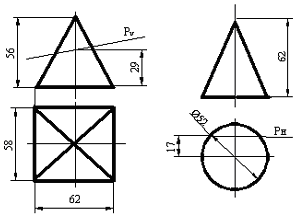
Сурет 108 Сурет 109

Конустың жанғы бетінің ұңғысы шеңберлі сектор болып келеді, радиусы конустың ұзындығына тең, доға секторының ұзындығы негізгі конустың айналасына тең. Конустың жанғы бетінің ұңғысын негізгі конустың айналасын 12 бірдей бөлікке бөліп доға радиусын 12 хордқа ауыстырып жақындатуға болады.

Тапсырманың нұсқасы 7-кестеде берілген.

7 кесте - Қима бетін құрастыру үшін мәліметтер

Нұсқа1	Нұсқа 2
Нұсқа 3	Нұсқа 4
Нұсқа 5	Нұсқа 6
Нұсқа 7	Нұсқа 8
Нұсқа 9	Нұсқа 10
Нұсқа 11	Нұсқа 12
Нұсқа 13	Нұсқа 14
Нұсқа 15	Нұсқа 16
Нұсқа 17	Нұсқа 18
Нұсқа 19	Нұсқа 20
Нұсқа 21	Нұсқа 22
Нұсқа 23	Нұсқа 24
Нұсқа 25	Нұсқа 26

5. Беттердің қиылысуы

5.1 «Беттердің қиылысуы» тақырыбына арналған қысқаша нұсқамалар

Техникада абсолюттік бөлшектің көбі формаға ие, өзімен геометриялық формасының қарапайым түрінде, белгіленген түрмен біріккен екіншісіне ауысады. ℓ түзуінің құрылуының жалпы алгоритмі және беттердің қиылысуы мынаған келеді:

1. Р₁ сыбайласты геометриялық элементі беріледі (арашашы), жоғарғы екі тапсырмаларымен қиылысады.

2. Әр бетпен бөлек m₁ және n₁ түзулері Р₁ арашашымен қиылысады.

3. m₁ және n₁ түзу қиылысы 1,1_* нүктеледі орналасқан.

Берілген алгоритм қажет мөлшерде қайталанады 2,2_*, 3,3_*…ί,ί_*, нүктелердің қажетті санын алғанша іздеген ℓ түзуін конфигурациясын сипаттайтын.

Белгіленгеннен кейін (тексеріс) көру нүктелері және олардың сұрақ шешімінің кезекпен қосылу арқылы іздеген қисық сызықты өткіземіз.

Арашашы ретінде жазықтық (арашашы жазық әдісі) қабылда алады, конустар, цилиндрлер, сфералар (шоғырлау әдіссферасы) және тағы басқа геометриялық элементтерге қатысты графикалық нақты тапсырмалар.

Арашашы жазық әдісінің мәні, арашашы ретінде жазықтықты қабылдау, ережеге сәйкес жеке орналасуы (деңгейі).

Кейбір жағдайларда арашашы жазықтың бағыты, дәл сол бірдей тапсырманың шешіміне сәйкес келмеуі.

1. Тіреу нүктелерді анықтау басынан құру керек – нүктелер, очерг бетінде орналасқан бейнелер (қисық проекциясының шектерін анықайтын нүктелер); нүктелер, жазық проекциясынан максимальды және минимальды қашықтықта жойылған (жоғарғы, төменгі, сол жақ, оң жақ, таяулау, алыстау және т.б.). Егер іздеп отырған түзу қиылысуын анықтауға, тіреу нүктелері жеткіліксіз болатын болса, онда еркін нүктелерді табу қажет.

Алгоритм шешілу символикасы былай көрсетеді:

1. α₁ ∩ Φ₁ = m₁; α₁ ∩ Φ₂ = n₁; m₁ ∩ n₁ = 1, 1_* - бірінші қадам;

2. α₂ ∩ Φ₁ = m₂; α₂ ∩ Φ₂ = n₂; m₂ ∩ n₂ = 2, 2_* - екінші қадам және т.б.

α_ķ ∩ Φ₁ = m _ķ; α_ķ ∩ Φ₂ = n _ķ; m _ķ ∩ n _ķ = ķ, ķ _* - соңғы қадам;

қайда ķ, ķ _* - аралық нүктелер. ℓ = 1, 1_*, 2, 2_*… ķ, ķ _*