Толықтыруға арналған тест түріндегі сұрақтар

Сұрақ 1. Перпендикулярдың бір мезгілде екі жазықтықтың және, параллелді үшінші жазықтық проекциясы, ... жазықтығы болып табылады.

Сұрақ 2. Сызықтың берілген жазықтықпен жазықтықтың қиылысуы ... деп аталады.

Сұрақ 3. Бірде-бір жазықтық проекциясымен параллель және перпендикуляр болмайтын жазықтық, ... жазықтығы деп аталады.

Сұрақ 4. Бір жазықтық проекциясымен перпендикуляр болатын жазықтық, ... деп аталады.

Сұрақ 5. Жазықтықтың жалпы орналасуы үш жазықтықты системада ... іздері болады.

Сұрақ 6. Көлденең параллельді жазықтықтар арақашықтығы шынайы өлшемде ... жазықтығында белгіленеді.

Сұрақ 7. Сызықтың көлденең-проекциялайтын жазықтықпен көлденең жазықтық проекциясының қиылысуы ... деп аталады.

Сұрақ 8. Көлденең жазықтықта орналасқан сопақ проекциялық профилінің деңгейі, ... формасында болады.

Сұрақ 9. Фронтальдң-проекциялық жазықтықта орналасқан үшбұрышты проекциялық профилінің деңгейі, ... формасында болады.

Сұрақ 10. Көлденең-проекциялық жазықтықта орналасқан шеңберлі проекциялық профилінің деңгейі, ... формасында болады.

Сұрақ 11. Көлденең-проекциялық жазықтықта орналасқан үшбұрышты фронтальді проекцияның деңгейі, ... формасында болады.

Сұрақ 12. Фронтальді-проекциялық жазықтықта орналасқан шаршылы фронтальді проекцияның деңгейі, ... формасында болады.

Сұрақ 13. Егер жазықтықтың көлденеңі бір мезгілде оның профилі болып табылса, ондай жазықтық ... орналасады.

Сұрақ 14. Егер жазықтықтың көлденеңі бір мезгілде оның фронталі болып табылса, ондай жазықтық ... орналасады.

Сұрақ 15. Егер жазықтықтың фронталі бір мезгілде оның профилі болып табылса, ондай жазықтық ... орналасады.

Сұрақ 16. Көлденең жазықтықта орналасқан үшбұрышты фронтальді проекцияның деңгейі, ... формасында болады.

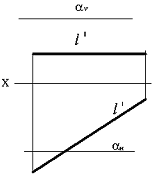
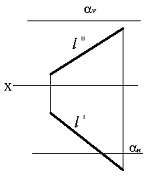
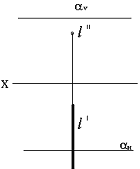
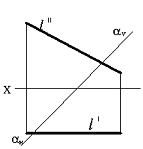
Сұрақ 17. Фронтальді жазықтық проекциясының параллеьді түзуі, ... деп аталады.

Сұрақ 18. Көлденең жазықтық проекциясының параллеьді түзуі, ... деп аталады.

Сұрақ 19. Кешенді сызбаны қайта жасауда фронтальді жазықтық проекциясын ауыстыруда ... мағынасына қатысты өзгермейді.

Сұрақ 20. Кешенді сызбаны қайта жасауда көлденең жазықтық проекциясын ауыстыруда тұрақты мағынасын құрастыру ... нүктелердің қайта жасау жүйесі.

Сұрақ 21. Көлденең жазықтыққа жалпы түзу орналасқан бұрыштық еңкіштің шынайы үлкендігін ... (жазықтық проекциясының ауыстыру әдісімен) ауыстыру керек.

Сұрақ 22. Фронталді жазықтық проекцияға жалпы түзу орналасқан бұрыштық еңкіштің шынайы үлкендігін жазықтық проекцияны ауыстыру әдісімен анықтау үшін ... жазықтық проекциясын ауыстыру қажет.

Сұрақ 23. Профильді жазықтық проекциясының параллельді түзуі, ... бар.

Сұрақ 24. Жазықтықты ... әдісімен белгілеуге болады.

Сұрақ 25. Жазықтықты түзулермен белгілеуге болады: ... және ... .

3.6 Графикалық модульге арналған тапсырма «Түзудің жазықтықпен қиылысуы»

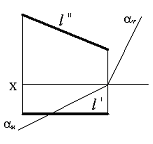
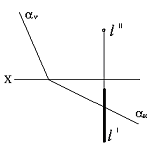
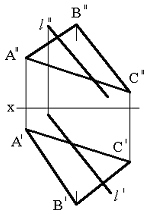
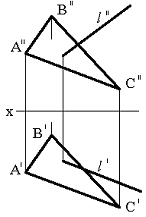
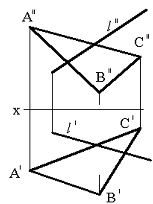
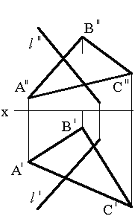
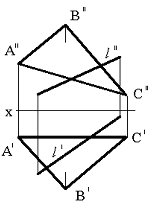
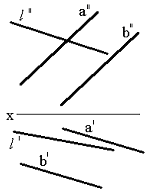
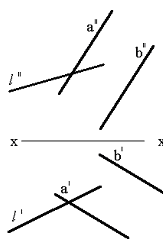
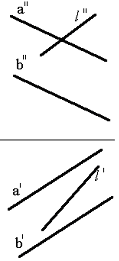
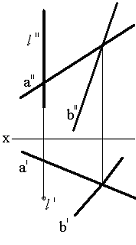
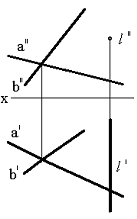
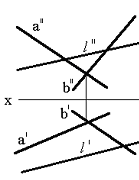
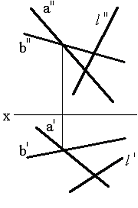
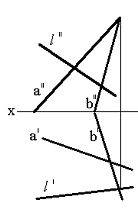
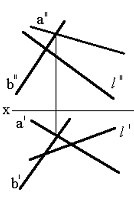
Тапсырма. Қиылысқан түзулермен берілген (75сур.) l нүктесінің жазықтықпен қиылысқан нүктесін табу.

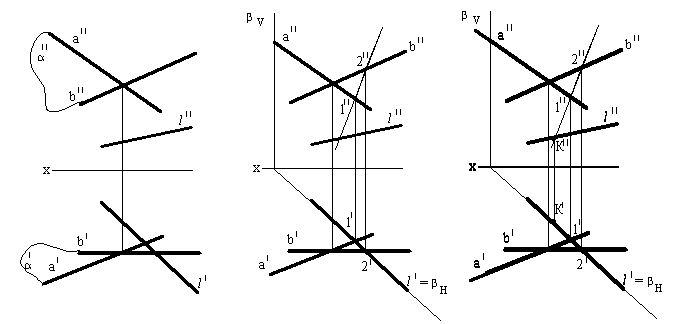
Сурет 75 Сурет 76 Сурет 77

Бұл тапсырманың шешімі жалпы жағдайда, жазықтықта, түзуде кеңістікте еркін орналасқан, оңай тоғысумен қарапайым тапсырманы екі жазықтықтың қиылысу түзуін анықтайды. Берілген - жазықтықтың біреуі, басқа – проекцияланған, l түзуі арқылы өткізу керек. Сондықтан бірінші кезең түзуді қорытындылаумен қосалқы проекцияланған жазықтық болады.

Шешім: 1. а′ (немесе а′′) көлденеңі (фронталі) арқылы β көлденең-проекцияланған (фронтальді-проекцияланған) жазықтығын өткңіземіз (76сур.).

2. β жазықтығының берілген α жазықтығымен фронтальді проекциялық (көлденең) қиылысу сызығын анықтаймыз. Бұл 1-2 түзуі.

3. а′′ фронтальді проекция түзуінің және l′′ фронтальді проекция түзуімен қиылысуын ізделінетін К нүктесі арқылы анықтаймыз. К нүктесінің фронтальді проекциясын ала отырып түзу байланысы арқылы көлденең проекцияны табамыз.

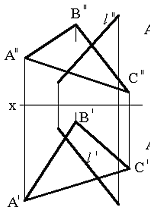
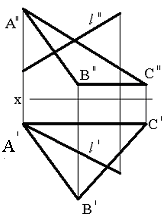
78-суретте α жазықтығы ізбен берілген. Бірінші кезеңде берілген (79сур.) l түзуін проекцияланған β жазықтығымен келістіреміз (көлденең проекцияда). Ары қарай қиылысқан 1-2 екі жазықтық α және β түзуін іздейміз. Соңғы кезеңде (80сур.) l түзуімен 1-2 түзуінің қиылысқан К нүктесін табамыз(фронтальді проекцияда).

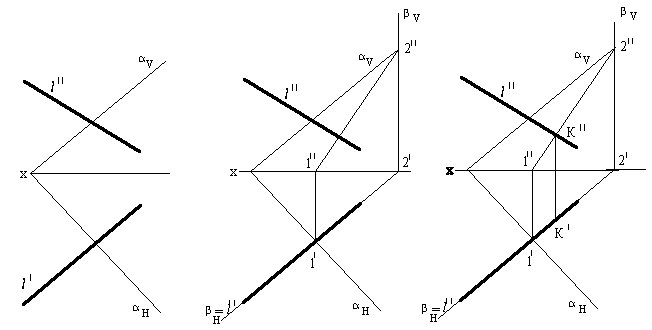
Сурет 78 Сурет 79 Сурет 80

Тапсырмалардың нұсқалары 3-кестеде берілген. Тапсырма А4 фарматында орындалады.

Символ бойынша жазылған алғашқы мәліметтер: жазықтық қандай әдіспен берілген. Тапсырманың шешімін символ түрінде жазу, нұсқаларын көрсету. Түзудің жағын анықтау.

3 кесте – Түзудің жазықтықпен қиылысқан мәліметтері