4. Арифметичні дії над додатніми раціональними числами

Означення. Якщо додатні раціональні числа а і b представлені дробами 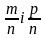, то сумою чисел а і b називається число .

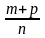(1)

Якщо додатні раціональні числа а і b представлені дробами з різними знаменниками, то ці дроби зводять до найменшого спільного знаменника і додають

Н.:

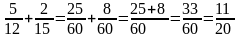
Закони додавання:

1. Переставний: а + b = b + a.

2. Сполучний: (a + b) + c = a + (b + c).

Дріб називається правильним, якщо його чисельник менше знаменника, а неправильним, якщо його чисельник більше знаменника або дорівнює йому.

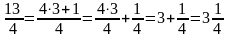
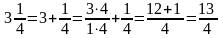
Означення. Різницею додатних раціональних чисел а і b називається таке додтнє раціональних число с, що а = b + с.

Нехай а = , b = , а різниця а – b нехай записується дробом 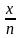. Знайдемо х. По визначенню різниці , а по правилу додавання 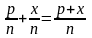. Таким чином, m = p + x, але m, p, x – числа натуральні, а для них цей запис означає, що x = m – p.

Тобто

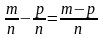(2)

Означення. Якщо додатні раціональні числа представлені дробами 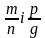, то їх добутком є число, записане дробом .

(3)

Закони множення:

1. Переставний закон .

2. Сполучний закон:

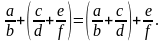
3. Розподільний закон множення відносно додавання і віднімання:

Приклади :

1)

2)

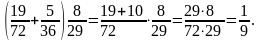
Означення. Часткою двох додатніх раціональних чисел а і b називається таке число с, що а = b · с.

Правило. Щоб поділити одне число, виражене дробом, на друге, треба чисельник першого дробу помножити на знаменник другого дробу і добутий результат взяти чисельником, а знаменник першого дробу помножити на чисельник другого дробу і одержаний результат взяти знаменником частки, або інакше, треба помножити на число, обернене дільнику:

(4)

Наприклад.

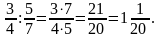
Це правило поширюється і на випадок ділення на натуральне число:

Риску в записі дробу розглядають як знак дії ділення.

Так як = m : n, то будь-яке додатнє раціональне число можна розглядати, як частку двох натуральних чисел.

Основна властивість частки

Якщо ділене і дільник помножити або поділити на те саме, відмінне від нуля і виражене дробом число, то значення частки не зміниться, тобто

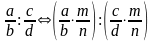, де

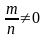
1) Щоб поділити суму (різницю) двох дробових чисел на третє дробове число, досить поділити на це число кожний доданок (змен­шуване і від’ємник) і знайдені частки додати (відняти), тобто

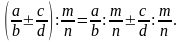
Наприклад.

2) Щоб поділити на дробове число добуток двох дробових чисел, досить поділити на це число один із співмножників і частку помно­жити на другий співмножник:

Наприклад.

3) Щоб поділити дробове число на добуток двох дробових чисел, досить поділити його послідовно на кожний із співмножників, тобто

4) Щоб поділити дробове число на частку від ділення двох дробо­вих чисел, досить поділити це число на ділене і помножити на дільник, тобто

Наприклад.

Отже, над дробами можна виконувати такі ж арифметичні дії, як і над натуральними числами.

Питання для узагальнення

• Які дії можна виконувати над дробами?

• Як додаються дроби?

• Як поділити дроби?

• Яка основна властивість частки дробів?

• Який дріб називається правильним (неправильним)?