3.6. Реализация метода конечных элементов в одномерном случае
Используемые данные:
-
число узлов;
- число элементов; координаты узлов –
массив
,
;
элементная матрица
размера
;
элементный вектор правых частей
,
;
глобальная матрица жесткости
размера
;
вектор правых частей
,
;
вектор решения
,
;
- координаты начала и конца отрезка, на
котором рассматривается уравнение;
- граничное условие.
Алгоритм
Вычисляем координаты узлов: Шаг сетки
;
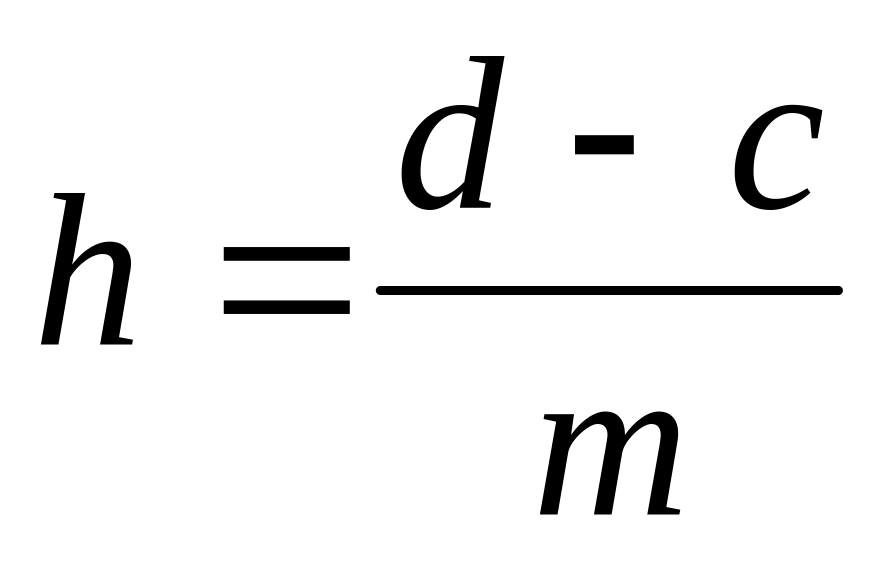Для
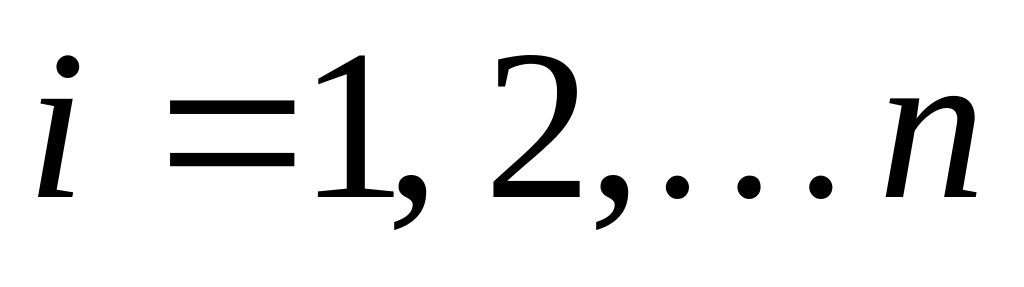
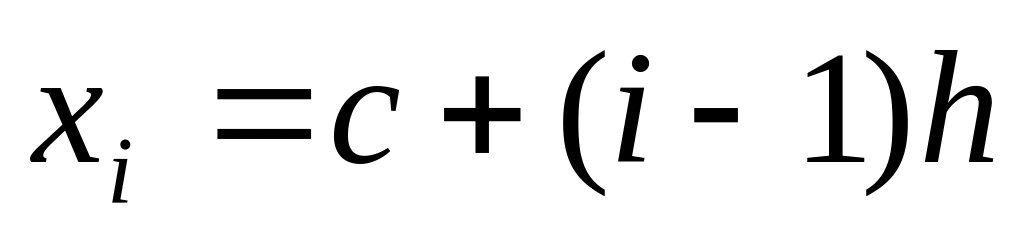;В цикле по элементам: Для
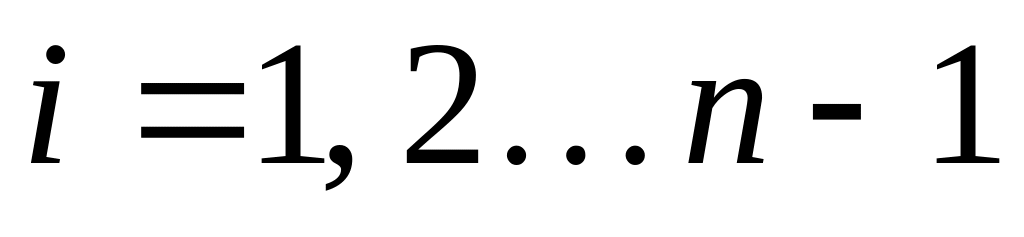
Формируем элементную матрицу .
Проводим процесс сборки – формируем глобальную матрицу жесткости
,
,
,
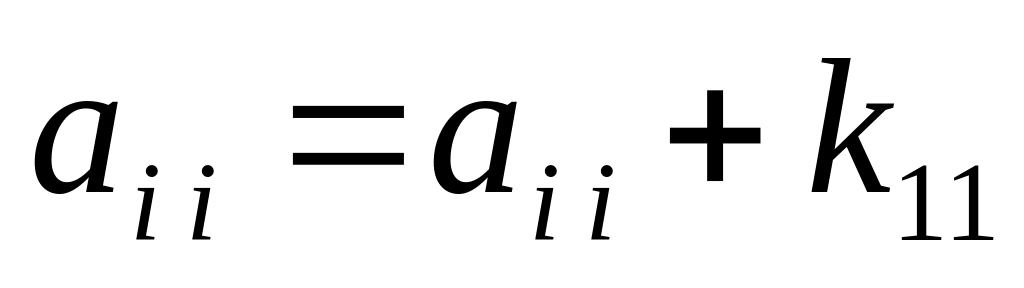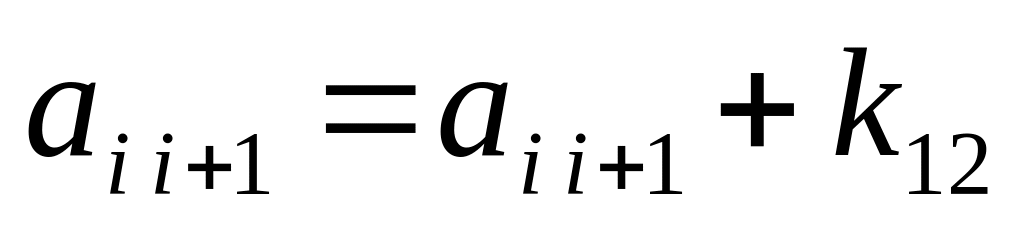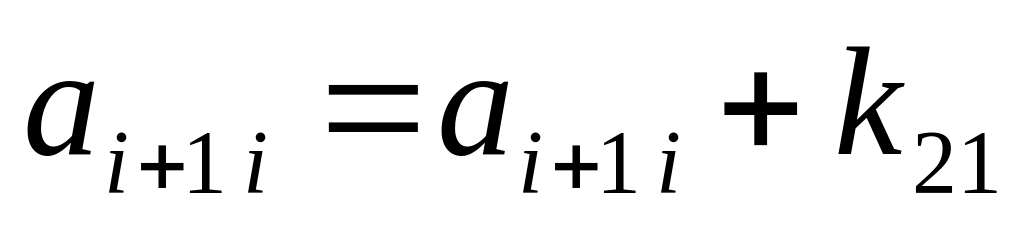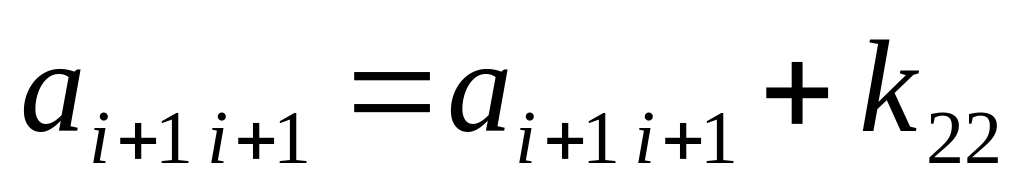.Формируем элементный вектор правых частей
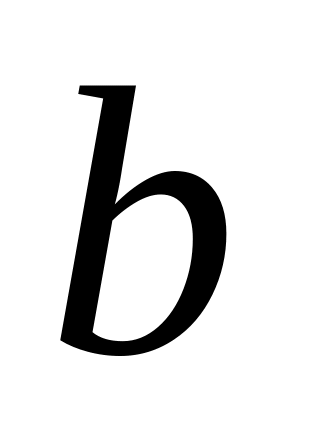.Проводим процесс сборки – формируем глобальный вектор правых частей
,
.
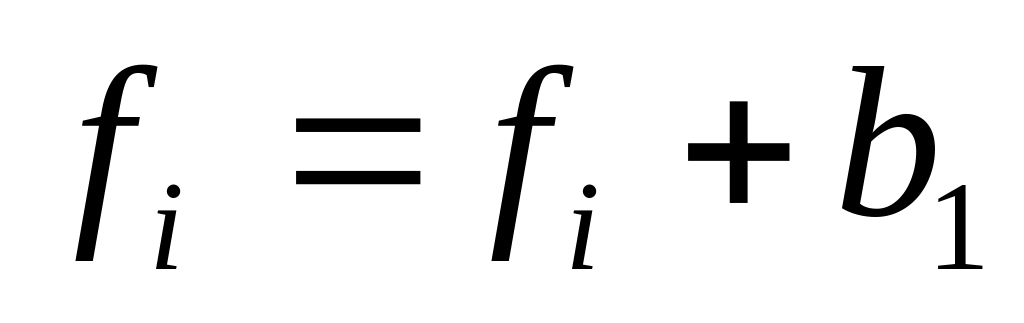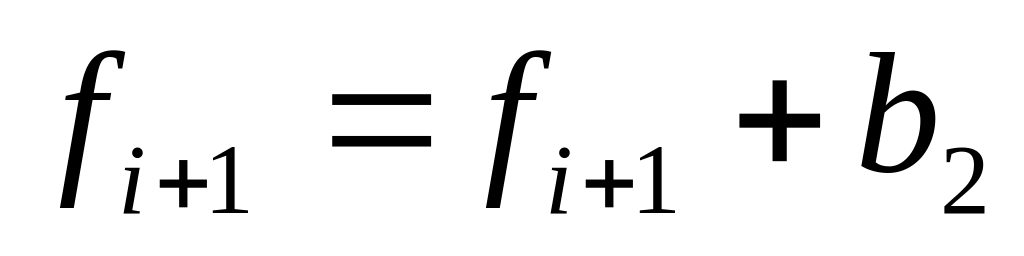Вносим граничное условие
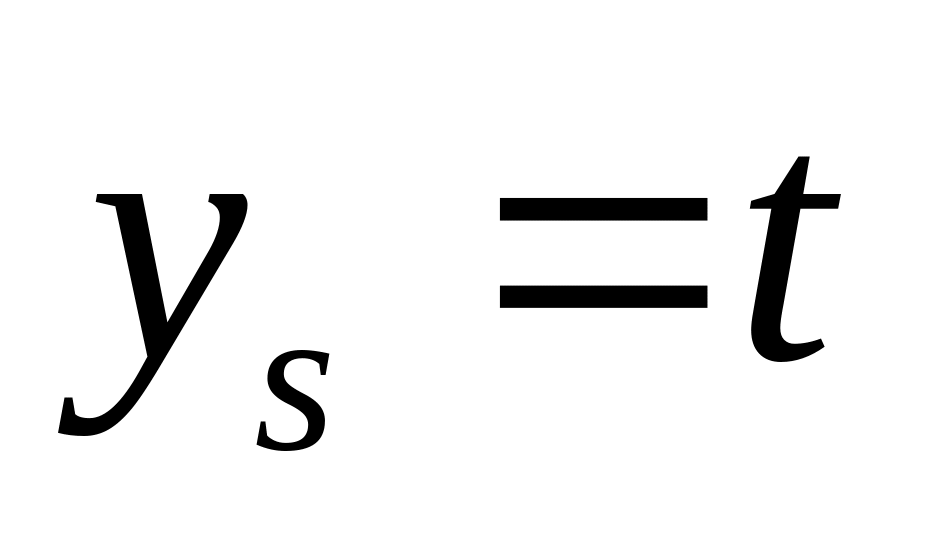в матрицу и вектор правых частей
;
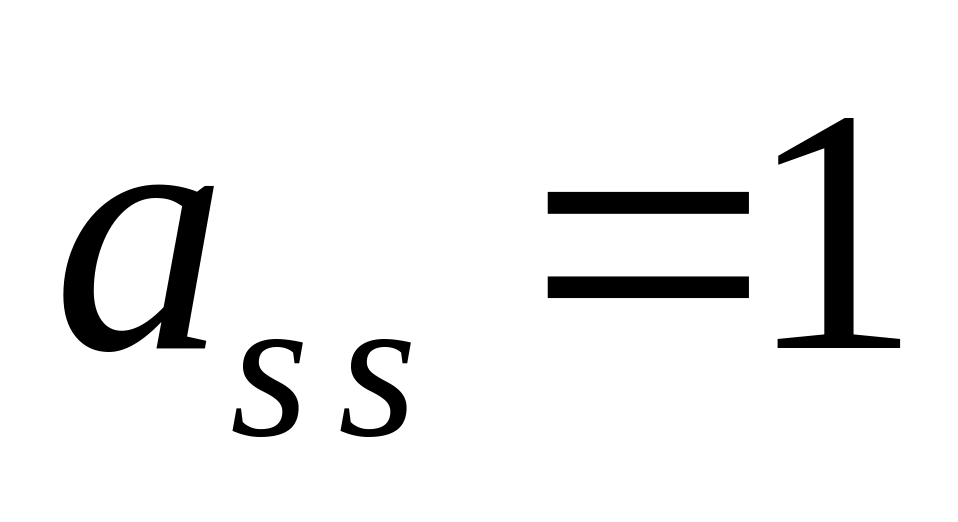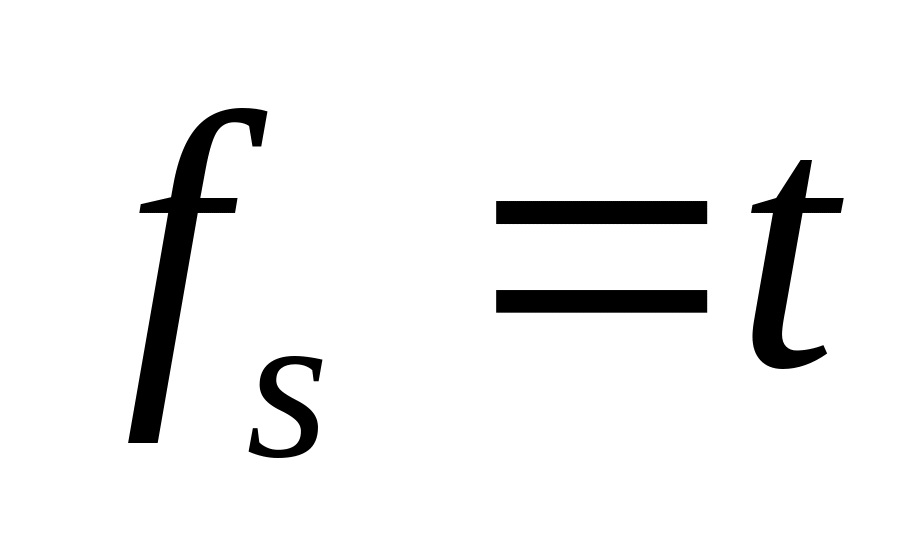;Для
,
;
;
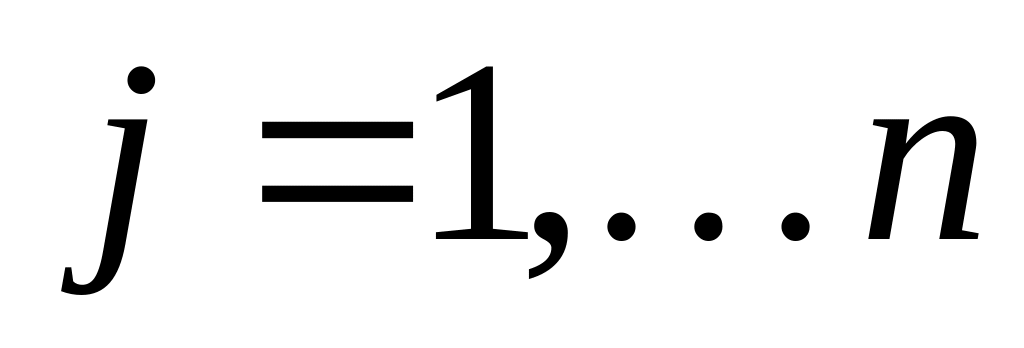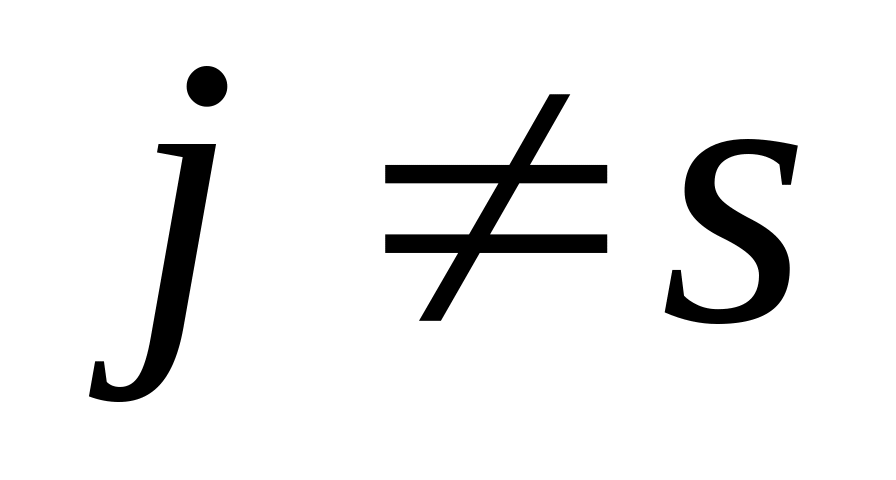
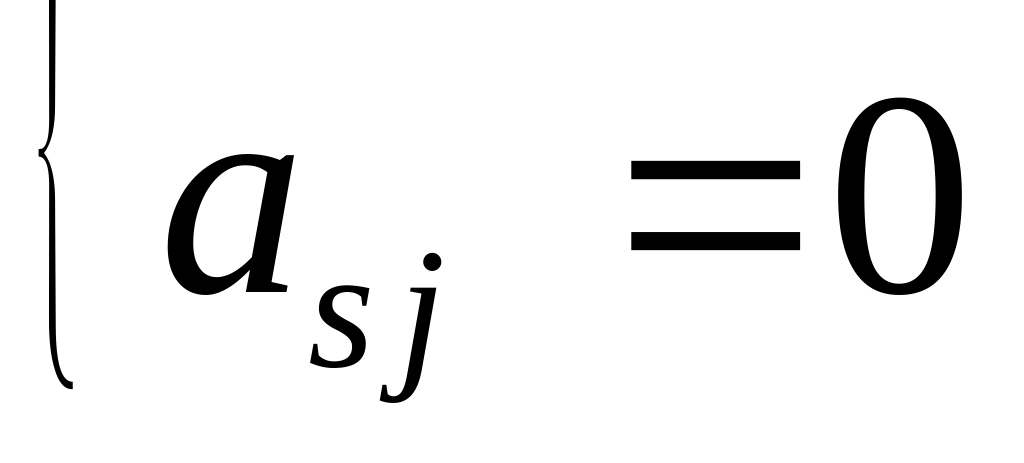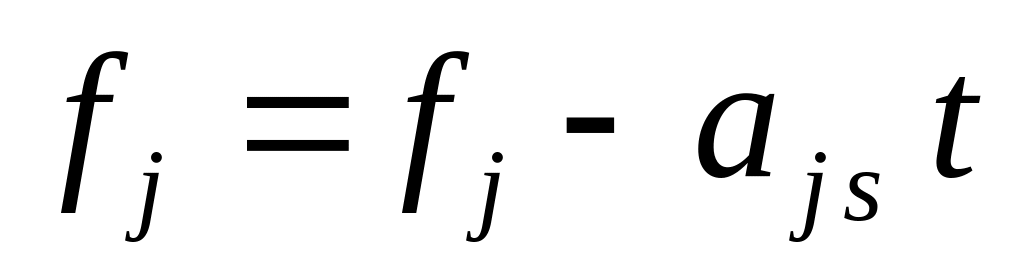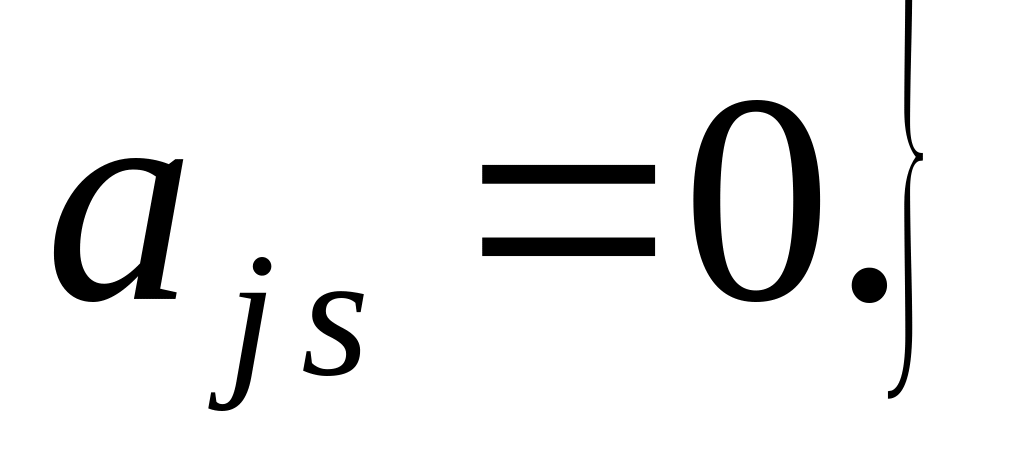
Решаем систему
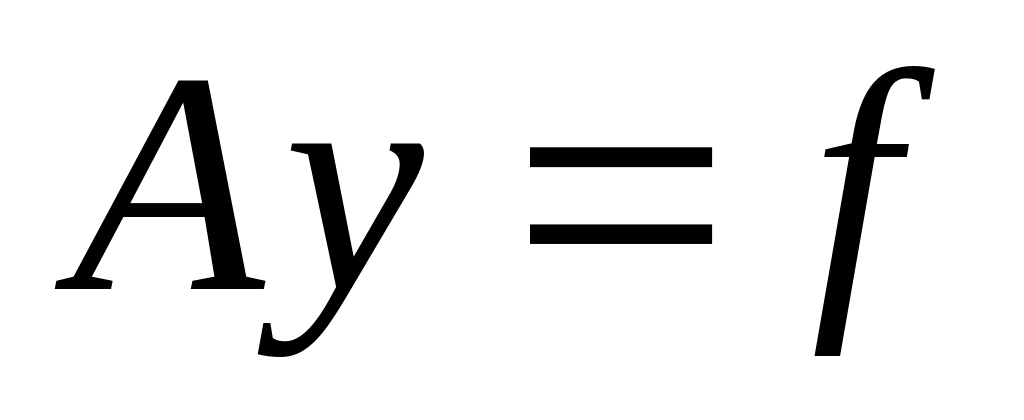.Выводим результат.
Приведем решение краевой задачи
, .
с помощью|посредством| программного комплекса MathCad:
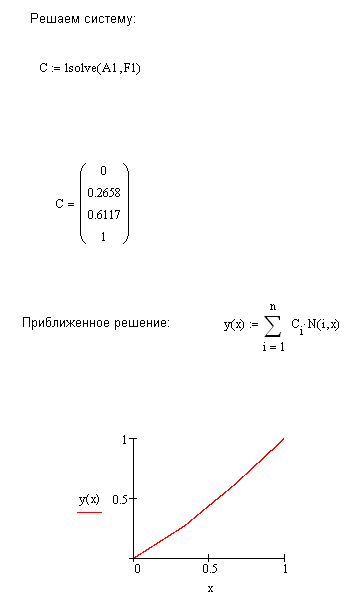
Сравним, значения точного и приближенного решений:
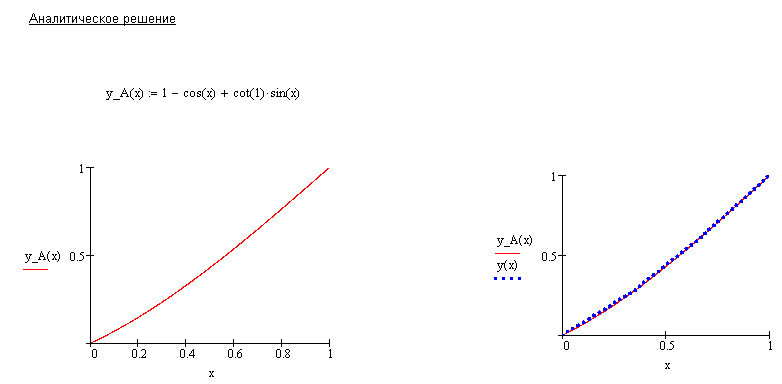
например, при имеем
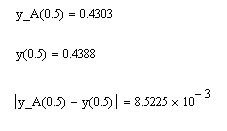
Как видим, погрешность близка к 0,85 %. Для получения более точного решения необходимо использовать большее количество базисных функций.
Варианты индивидуальных заданий
№ 1. Решить нелинейную систему уравнений методом Ньютона с точностью .
№ 2, №3. Решить краевую задачу методом Галеркина и методом конечных элементов
четные варианты : 
,
,
нечетные варианты: 
,
,
где
- номер варианта.
Список рекомендованной литературы
Демидович Б. П., Марон И. А. Основы вычислительной математики. – М.: Наука, 1970. – 664 с.
Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. – М.: БИНОМ, 2000. – 630 с.
Калиткин Н.Н. Численные методы. – М.: Наука, 1978. – 512 с.
Киреев В.И., Пантелеев А.В. Численные методы в примерах и задачах: Учебное пособие. – М.: Изд-во МАИ, 2000. – 376 с.
Мэтьюз Дж.Г., Финк К.Д. Численные методы: Использование MATLAB. – М.: Издательский дом «Вильямс», 2001. – 720 с.
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 2: Учеб. пособие для вузов – М.: ООО Издательский дом «ОНИКС 21 век»: ООО Издательство «Мир и Образование», 2003. – 416 с.
Эльсгольц Л.Э. Дифференциальные уравнения и вариационное исчисление. – М.: Наука, 1969. – 424 с.
Марчук Г. И., Агошков В.И. Введение в проекционно-сеточные методы. – М.: Наука, 1981. – 416 с.
Сагдеева Ю. А., Копысов С. П., Новиков А. К. Введение в метод конечных элементов. – Ижевск.: Изд-во «Удмуртский университет», 2011. – 44 с.
Зенкевич О., Морган. Конечные элементы и аппроксимации. – М.: Мир, 1986. – 318 с.
Норри Д., де Фриз Ж.. Введение в метод конечных элементов. – М.: Мир, 1981. – 304 с.
Министерство образования и науки, молодежи и спорта Украины
Донбасская национальная академия строительства и архитектуры
Методические указания
к самостоятельной работе по курсу «Численные методы решения инженерных задач»