3. Проекционные методы решения краевых задач для обыкновенных дифференциальных уравнений

Краевыми задачами называются задачи, в которых дополнительные условия задаются при двух значениях независимой переменной (на концах рассматриваемого участка).

Рассмотрим краевую задачу на примере обыкновенного дифференциального уравнения второго порядка

с граничными условиями

.

Сущность проекционных методов состоит в разложении решения по базису некоторых функций (проекций)

.

Базис выбирается в достаточной степени произвольно. В роли базисных функций могут выступать обычные полиномы , полиномы Лагранжа , Фурье-гармоники, наборы синусов и т.д.

Обязательные условия, которым должны удовлетворять базисные функции:

• разложение должно аппроксимировать ваше решение с любой, сколь угодно малой точностью (т.е. 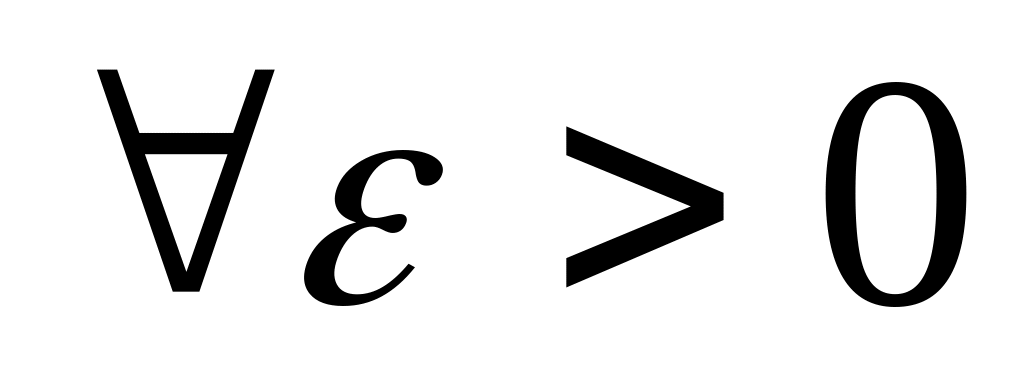существует такое , что норма отклонения );

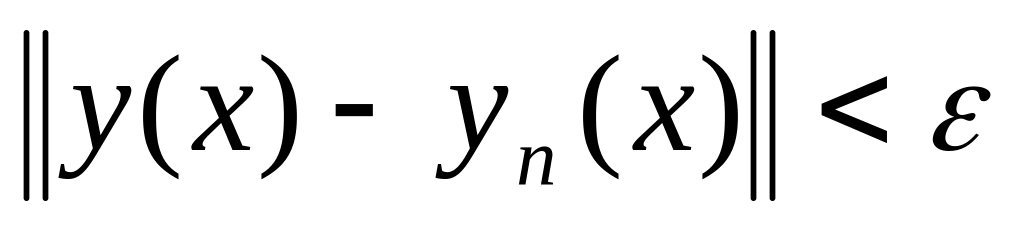• функции 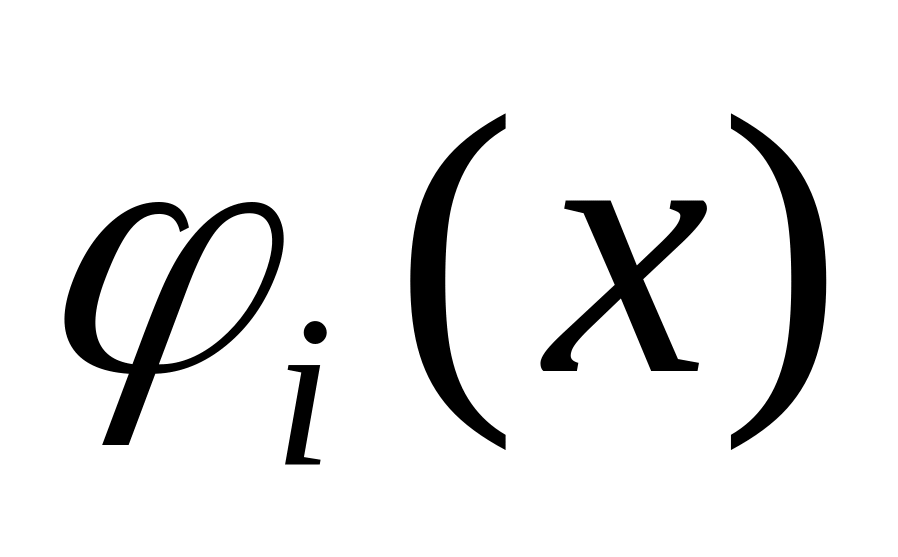должны быть линейно независимы;

• любая комбинация функций должна удовлетворять поставленным граничным условиям.

После выбора базисных функций разложение подставляется в исходное уравнение, и получается система для расчета неизвестных коэффициентов .

Недостатки проекционных методов:

• произвольность в выборе базиса (характер полученного решения в определенной степени определяется характером базисных функций);

• необходимость решения больших систем алгебраических уравнений.

Преимущества:

• решение находится сразу во всей области изменения независимой переменной, а не в отдельных точках;

• погрешность расчета одинакова во всем диапазоне изменения независимой переменной (отсутствует экспоненциальный рост погрешности, характерный для методов решения задачи Коши).

3.1. Метод Галеркина

Метод Галеркина используется для приближенного решения краевых задач для дифференциальных уравнений, как обыкновенных, так и в частных производных.

Рассмотрим краевую задачу

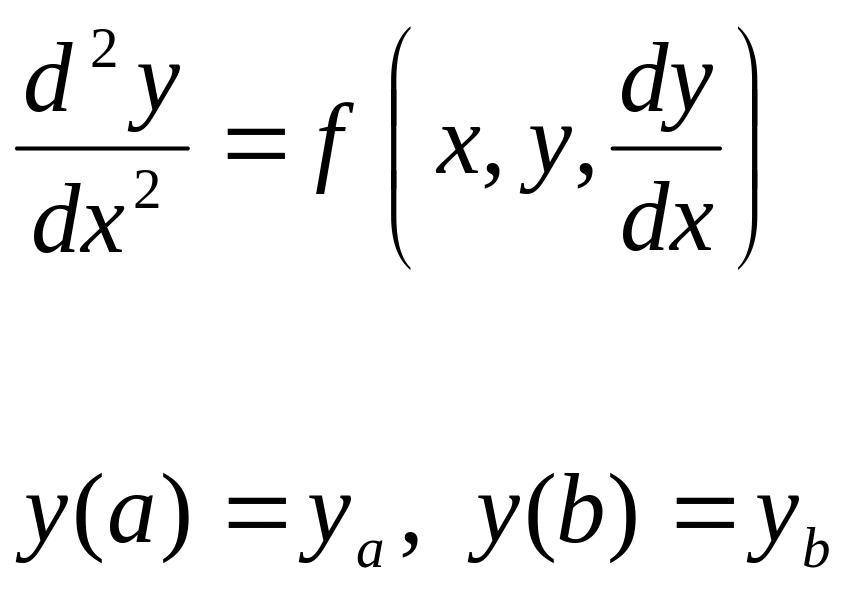(3.1)

Для ее приближенного решения выберем какую-либо последовательность базисных функций

(3.2)

т. е. последовательность функций, удовлетворяющих соответствующим однородным краевым условиям

и обладающих свойством полноты. Последнее означает, что любую функцию из достаточно широкого класса, удовлетворяющую указанным однородным краевым условиям, можно разложить в ряд по функциям (3.2).

Чаще всего полагают

или , .

Кроме того, надо выбрать какую-нибудь функцию , удовлетворяющую краевым условиям, указанным в (3.1), например,

или

Приближенное решение задачи (3.1) ищется в виде

, (3.3)

где функции , , … мы задаем, а постоянные , , … , подбираем. Тогда краевые условия, указанные в (3.1), заведомо удовлетворяются, а при подстановке выражения (3.3) в дифференциальное уравнение получается невязка (т. е. разность между левой и правой частями уравнения)

.

С ее помощью получаем систему из уравнений с неизвестными для определения

.