2.3. Линейные однородные уравнения с постоянными коэффициентами

Линейным однородным дифференциальным уравнением -го порядка с постоянными коэффициентами называется уравнение вида

(2.1)

где коэффициенты - некоторые действительные числа. Для нахождения частных решений уравнения (2.1) составляют характеристическое уравнение

, (2.2)

которое получается из уравнения (2.1) заменой в нем производных искомой функции соответствующими степенями , причем сама функция заменяется единицей. Уравнение (2.2) является уравнением -й степени и имеет корней (действительных или комплексных, среди которых могут быть и равные).

Тогда общее решение дифференциального уравнения (2.1) строится в зависимости от характера корней уравнения (2.2):

каждому действительному простому корню в общем решении соответствует слагаемое вида ;
каждому действительному корню кратности в общем решении соответствует слагаемое вида ;
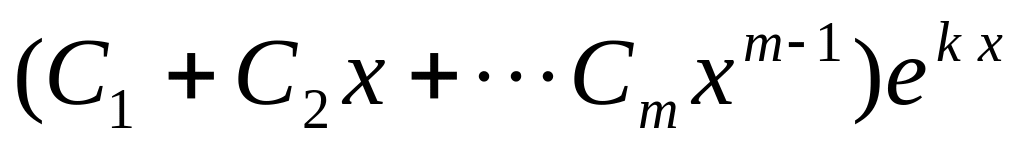каждой паре комплексных сопряженных простых корней и в общем решении соответствует слагаемое вида ;
каждой паре комплексных сопряженных корней и кратности в общем решении соответствует слагаемое вида ;

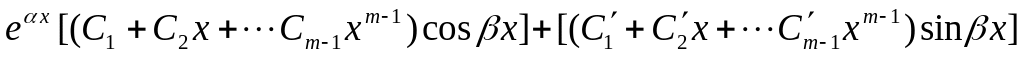2.4. Линейные неоднородные уравнения

Структура общего решения линейного неоднородного уравнения, т.е. уравнения с правой частью:

определяется следующей теоремой.

Если - частное решение неоднородного уравнения, а - фундаментальная система решений соответствующего однородного уравнения, то общее

решение линейного неоднородного уравнения имеет вид ; иными словами, общее решение неоднородного уравнения равно сумме любого его частного решения и общего решения соответствующего однородного уравнения.

Следовательно, для построения общего решения неоднородного уравнения надо найти одно его частное решение (предполагая уже известным общее решение соответствующего однородного уравнения).

Метод вариации произвольных постоянных. Этот метод применяется для отыскания частного решения линейного неоднородного уравнения -го порядка как с переменными, так и с постоянными коэффициентами, если известно общее решение соответствующего однородного уравнения.

Метод вариации заключается в следующем. Пусть известна фундаментальная система решений соответствующего однородного уравнения. Тогда частное решение неоднородного уравнения следует искать в виде