1.2. Реализация метода Ньютона в|посредством| MathCad

Пример. Решить нелинейную систему уравнений методом Ньютона

с точностью .

Приведем решение нелинейной системы уравнений с помощью|посредством| программного комплекса MathCad:

Номер первой строки (столбца) матрицы или первой компоненты вектора хранится в MathCad в переменной ORIGIN. По умолчанию в MathCad координаты векторов, столбцы и строки матрицы нумеруются начиная с 0 (ORIGIN:=0). Поскольку в математической записи чаще используется нумерация с 1, здесь и в дальнейшем перед началом работы с матрицами будем определять значение переменной ORIGIN равным 1, т.е. будем выполнять команду ORIGIN:=1. Далее определяем функции F1 и F2 нелинейной системы и находим графическое решение системы.

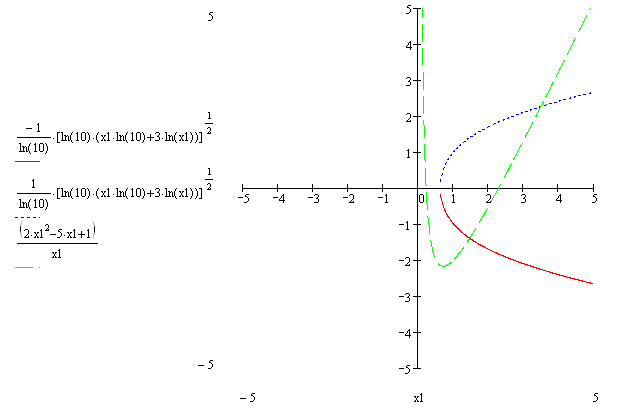
Процесс отыскания корней системы при помощи метода Ньютона организован в виде функции, входные параметры которой – вектор начальных приближений x0 и точность вычислений ( ), где за x0 можно взять грубое значение искомого корня – приблизительные координаты точки пересечения графиков функций: – грубое значение первого корня, затем – грубое значение второго корня.

2. Дифференциальные уравнения высших порядков

2.1. Основные понятия

Дифференциальным уравнением - го порядка называется уравнение вида

.

Решением такого уравнения служит всякая раз дифференцируемая функция , которая обращает данное уравнение в тождество, т.е.

.

Задача Коши для этого уравнения состоит в том, чтобы найти решение уравнения, удовлетворяющее условиям , , …, при , где , , , …, - заданные числа, которые называются начальными данными, или начальными условиями.

Краевая задача для этого уравнения состоит в том, чтобы найти решение уравнения, удовлетворяющее граничным условиям. Эти условия (число которых не должно превышать порядка уравнения) задаются не в одной точке, а на концах некоторого промежутка.

Функция называется общим решением данного дифференциального уравнения - го порядка, если при соответствующем выборе произвольных постоянных эта функция является решением любой задачи Коши (краевой задачи), поставленной для данного уравнения.

Всякое решение, получаемое из общего решения при конкретных значениях постоянных , называется частным решением этого уравнения.

Линейным дифференциальным уравнением - го порядка называется уравнение вида

.

Здесь функции , , …, и заданы и непрерывны в некотором промежутке .

Данное уравнение называется линейным неоднородным, или уравнением с правой частью. Если же , то уравнение называется линейным однородным. Однородное уравнение с той же левой частью, что и данное неоднородное, называется соответствующим ему.

2.2. Линейные однородные уравнения

Одним из замечательных свойств линейных уравнений является то, что общее решение таких уравнений можно найти по их известным частным решениям.

Теорема. Если - линейно независимые частные решения уравнения

,

то есть общее решение этого уравнения ( - произвольные постоянные).

Примечание. Функции называются линейно независимыми в промежутке , если они не связаны никаким тождеством

,

где - какие-нибудь постоянные, не равные нулю одновременно.

Для случая двух функций это условие можно сформулировать и так: две функции и линейно независимы, если их отношение не является постоянной величиной:

.

Достаточным условием линейной независимости функций, непрерывных вместе со своими производными до -го порядка в промежутке , является то, что определитель Вронского (вронскиан) этих функций не равен нулю ни в одной точке промежутка , т.е.

.

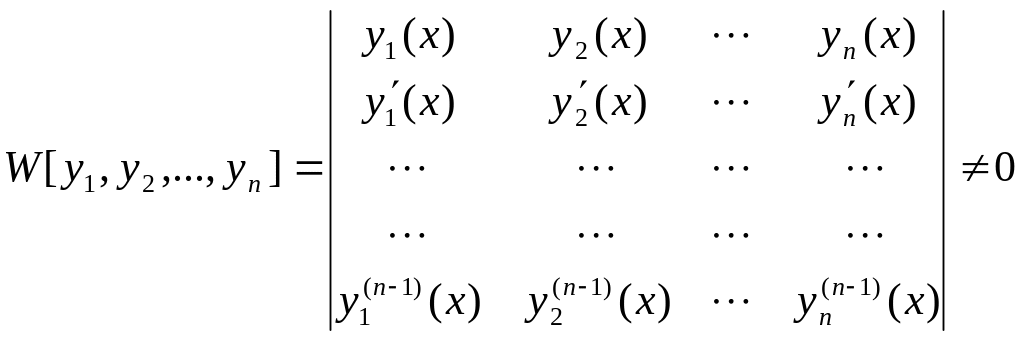Если данные функций являются частными решениями линейного однородного дифференциального уравнения -го порядка, то это условие (необращение в нуль) является не только достаточным, но и необходимым условием линейной независимости этих решений.

Вронскиан решений линейного однородного дифференциального уравнения -го порядка

связан с первым коэффициентом этого уравнения формулой Лиувилля-Остроградского:

Совокупность решений линейного однородного дифференциального уравнения -го порядка, определенных и линейно независимых в промежутке , называется фундаментальной системой решений этого уравнения.

Для линейного однородного дифференциального уравнения второго порядка

фундаментальная система состоит из двух линейно независимых решений и ; его общее решение находится по формуле

.

Если для такого уравнения известно одно частное решение , то второе его решение, линейно независимое с первым, можно найти по формуле (являющейся следствием формулы Лиувилля-Остроградского)

.

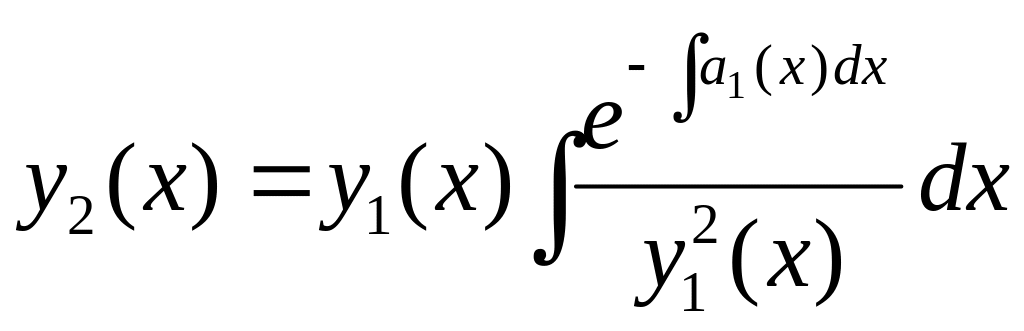Это дает возможность интегрировать линейные однородные уравнения второго порядка, для которых известно одно частное решение, сразу, не прибегая к понижению их порядка.