9.11. Предполагаемая кратность увеличения тока, обусловленная уменьшением индуктивных сопротивлений из-за насыщения зубцовых зон,
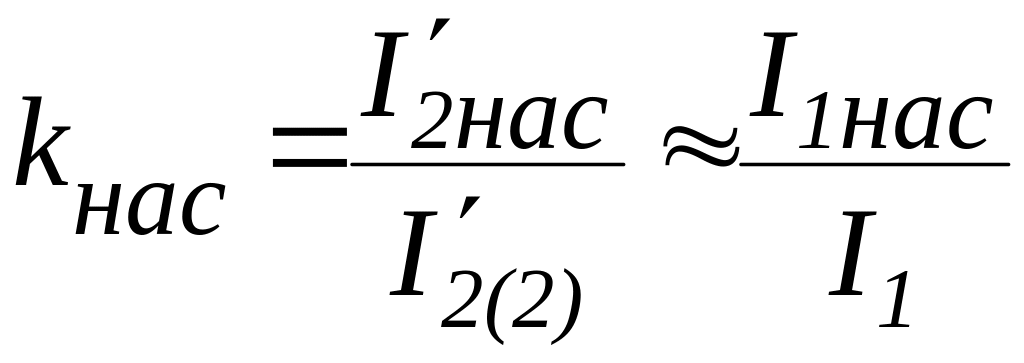
при s=1 принимается ориентировочно равной 1,25 1,4.
Для других значений скольжения определение коэффициента kнас рассматривается ниже.
9.12. Предварительное значение тока фазы статора с учётом насыщения, А
.
9.13. Средняя МДС обмотки статора, отнесённая к одному пазу, А
,
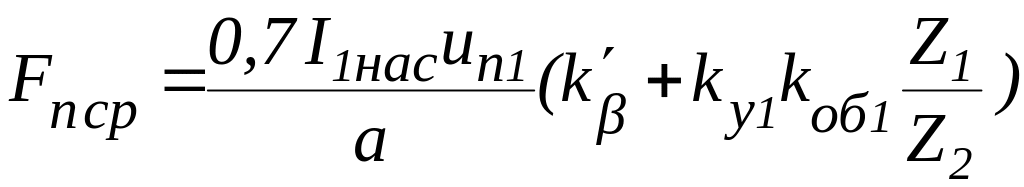где
,
,
,
,
,
,
a
из п.п. 2.4, 2.5, 6.6, 2.7, 2.1, 4.1.
9.14. Фиктивная индукция магнитного поля рассеяния в воздушном зазоре, Тл
,
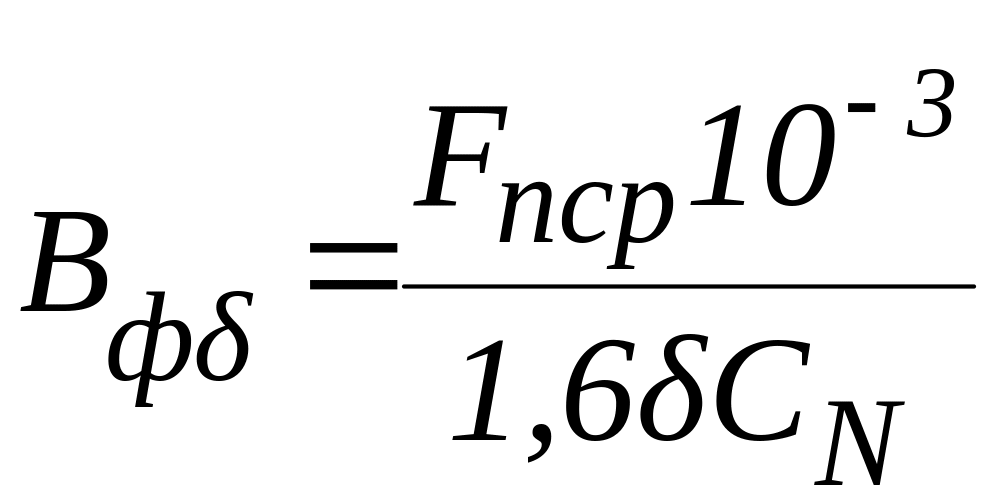где δ из п. 3.6; CN коэффициент, определяемый по формуле,
,
t1, t2 из п.п. 2.2, 4.4.
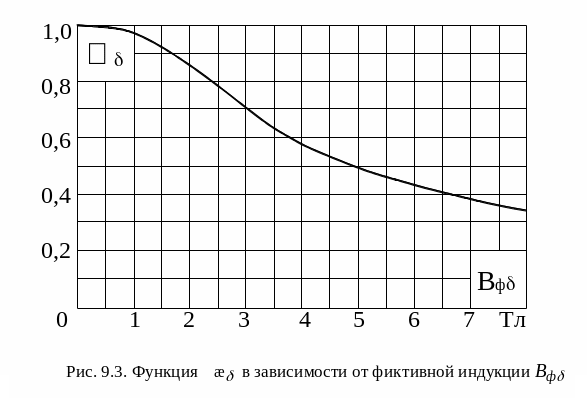
9.15. Коэффициент
æ
, равный отношению потока рассеяния
при насыщении к потоку рассеяния
ненасыщенной машины, находится по рис.
9.3.
9.16. Дополнительное раскрытие пазов ротора и статора, учитывающее уменьшение потока пазового рассеяния из-за насыщения, мм
,
,
где bш1 из п.3.2.
При 2р = 2, вследствие отсутствия в пазах ротора шлица, с2 не определяется.
9.17. Уменьшение коэффициента магнитной проводимости пазового рассеяния статора и ротора, вызванное насыщением коронок зубцов,
,
,
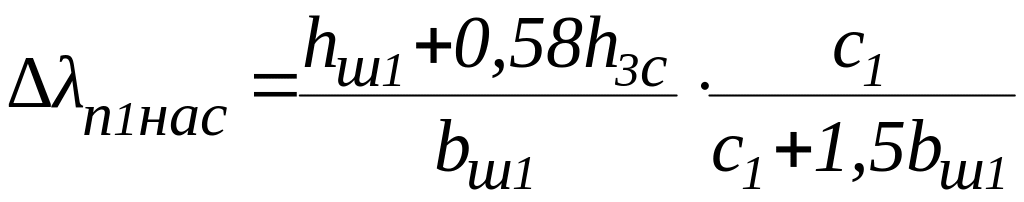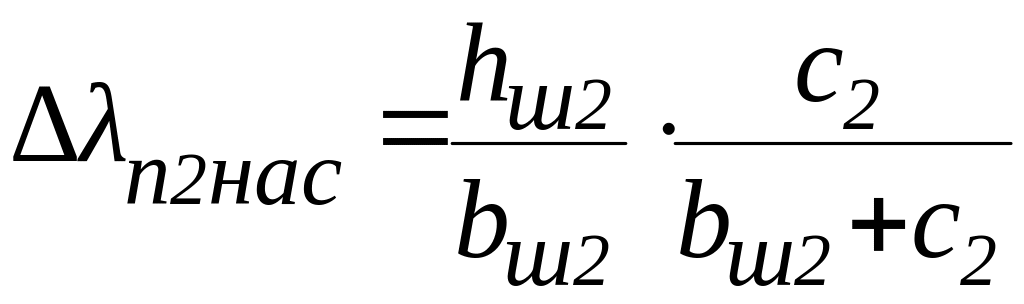где
,
,
,
из п.п. 3.2, 3.3, 4.6.
9.18. Коэффициент магнитной проводимости дифференциального рассеяния статора и ротора при насыщении
,
,
где λп1
из п. 6.6. При 2р
= 2 шлиц в пазах ротора отсутствует,
поэтому принимается
.
9.19. Коэффициент магнитной проводимости дифференциального рассеяния статора и ротора при насыщении зубцов
,
,
где λд1, λд2 см. п.п. 6.6, 6.8.
9.20. Индуктивные сопротивления обмотки статора с учётом насыщения и обмотки ротора с учётом влияния насыщения и вытеснения тока, Ом
,
,
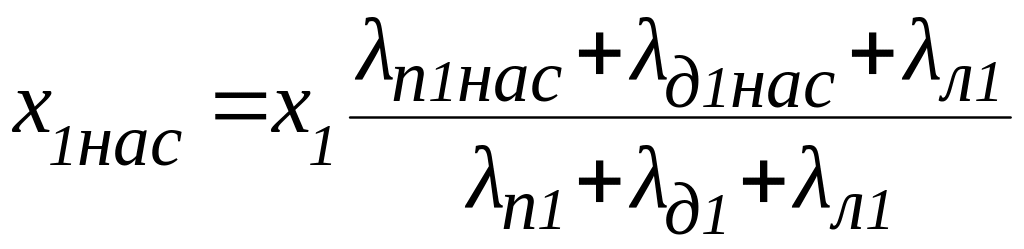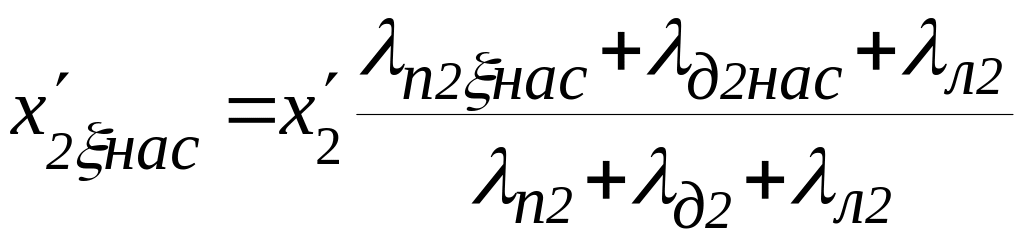см. п. 6.6 и 6.8.
9.21. Коэффициент связи параметров Г-образной и Т-образной схем замещения
,
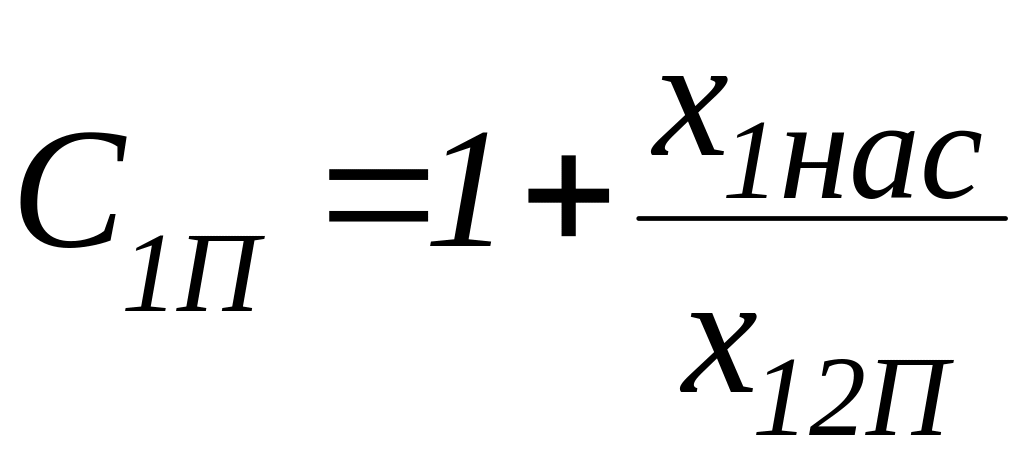где
сопротивление
взаимной индукции обмоток при s
≥ 0,1; значения
x12,
Fδ,
Fц
из п.п.8.3, 5.3, 5.8.
9.22. Расчетные активное и индуктивное сопротивления, Ом
,
.
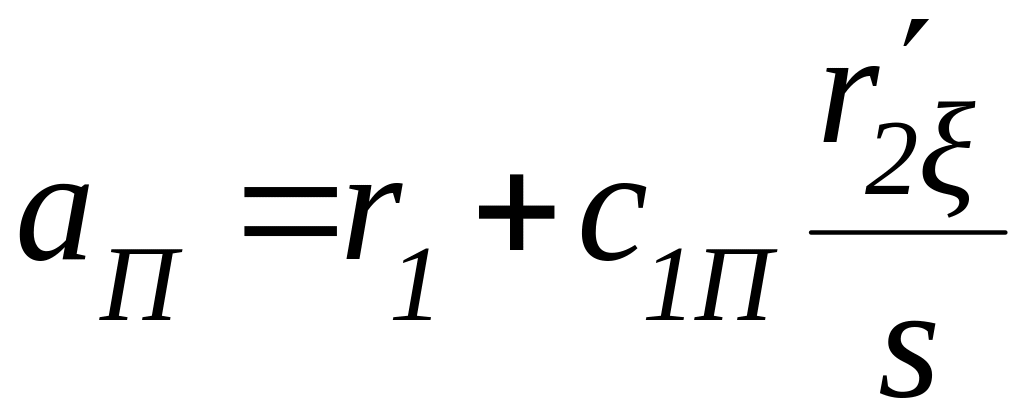9.23. Ток обмотки ротора, приведенный к обмотке статора, А
.
9.24. Ток обмотки статора, А
.
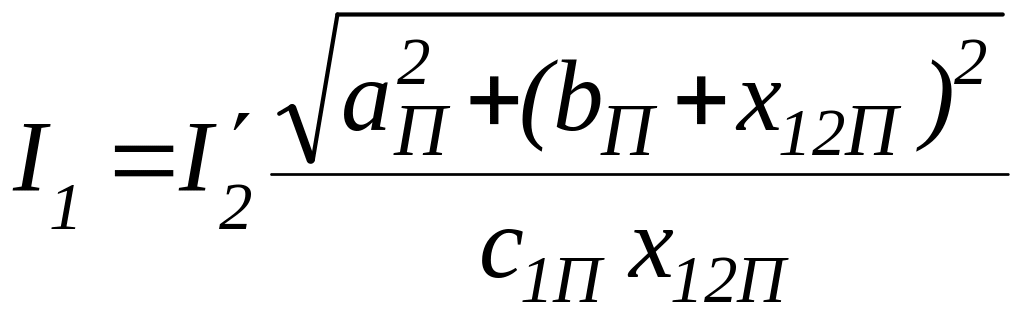9.25.
Расхождение полученных значений
и
и принятых первоначально
(п.9.12) и
(п.9.7), %
,
.
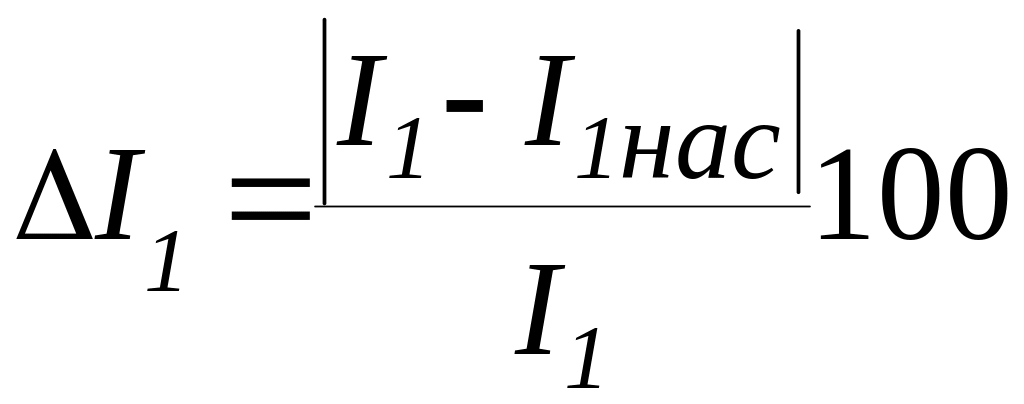Если расхождения не превышают 15%, расчет токов считают законченным. При больших расхождениях повторяют расчет п.п. 9.7, 9.11…9.25, задавшись новыми значениями и , равными из п. 9.23 и из п. 9.24, соответственно.
9.26. Относительные значения тока статора и электромагнитного момента
,
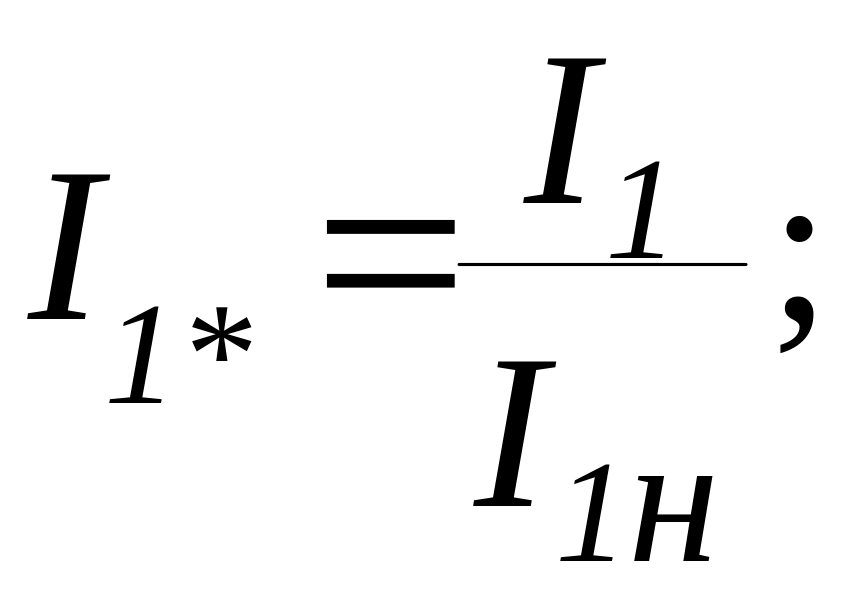
где
определяются по рабочим характеристикам,
см. п. 8.23.
Величины
и
при s
= 1 представляют собой кратности пускового
тока
и пускового момента
.
Эти показатели должны быть не хуже (
не более, а
не менее) требований ГОСТ
19523-81 (см. приложение 1). Если полученные
значения не удовлетворяют этим
требованиям, дальнейшие действия
следует согласовать с преподавателем.
9.27. Расчет пусковых характеристик для критического скольжения производится аналогично с учётом следующих дополнений.
Значение критического скольжения в первом приближении можно определять по формуле
,
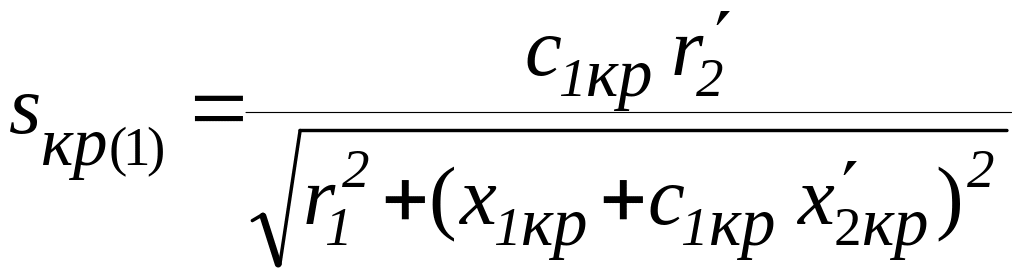где
,
и
предварительно определяются по формулам
.
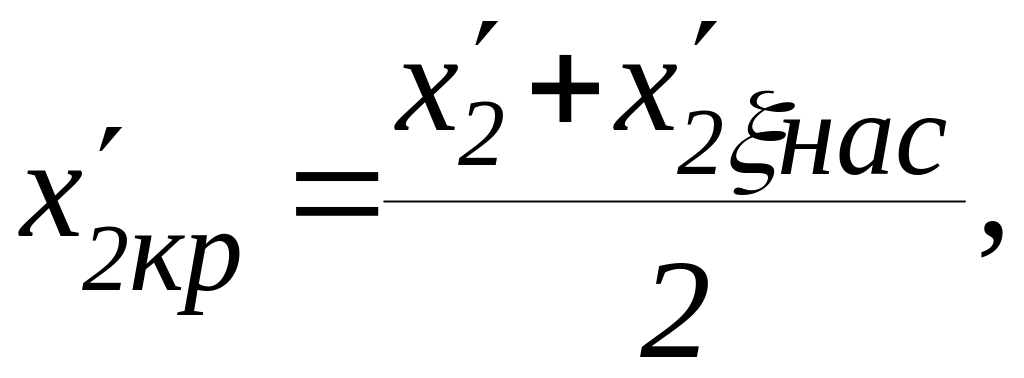
Здесь
используются значения
из п.п. 6.2, 6.4, 6.7, 6.9, 9.21, а также
из п. 9.20 при
.
Для
полученного значения
рассчитываются п.п. 9.1 … 9.21. При этом в
п. 9.7 приближенное значение тока ротора
определяется по формуле, А
,
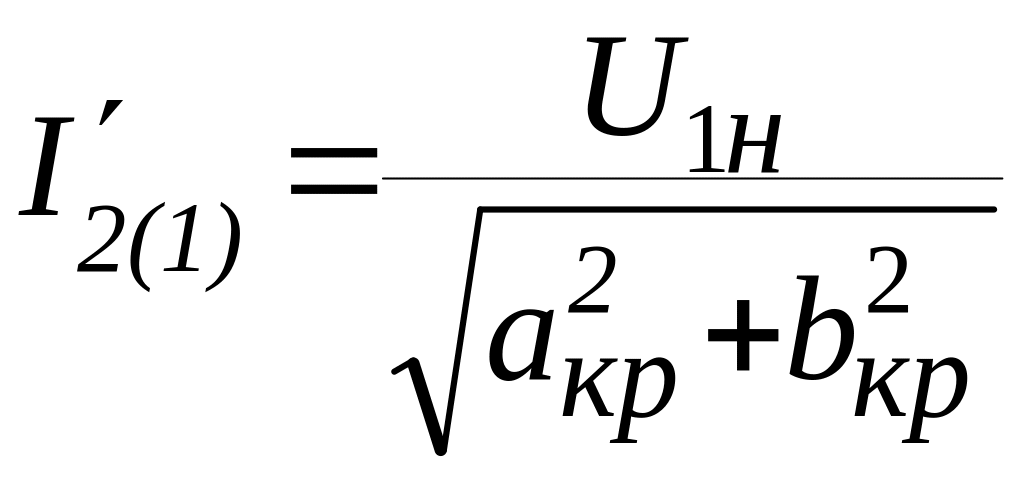где
и
рассчитываются по формулам, Ом
.
В
п. 9.11 следует принять
= 1,11..1,15.
После п. 9.21 уточняется значение критического скольжения по формуле
,
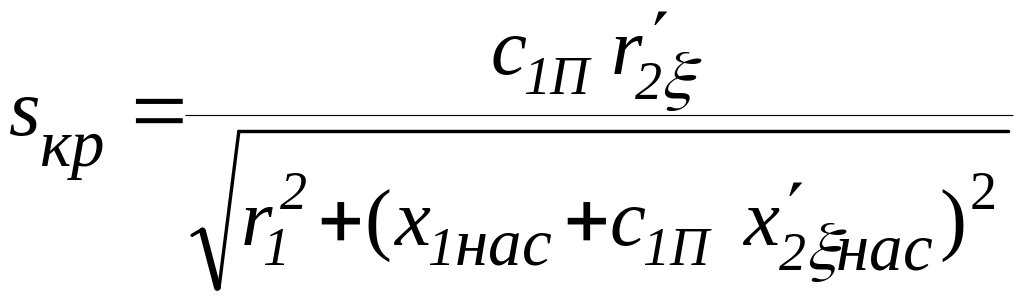в
которую в качестве
,
подставляются значения параметров из
п. 9.6, 9.20 и 9.21, вычисленные при
.
Далее
рассчитываются п.п. 9.22…9.26 при
.
Полученное
в п. 9.26 значение
при
представляет собой кратность максимального
момента
.
Для
студентов заочной формы обучения расчет
пусковых характеристик на этом
заканчивается. Пусковые характеристики
можно приближенно построить по известным
данным для четырёх значений скольжения:
=0
;
;
и s=1.
Примерный вид пусковых характеристик
приведен на рис. 9.4.
9.28. Расчет пусковых характеристик для остальных заданных значений скольжения 1>s>0 производится аналогично с учётом того, что значения тока ротора в п. 9.7 и коэффициента влияния насыщения в п. 9.11 следует определять по формулам
,
,
,
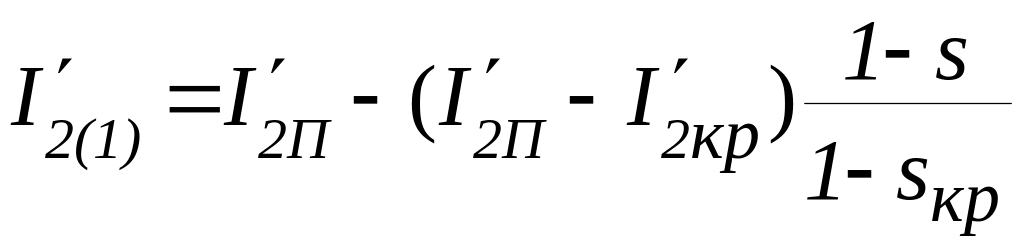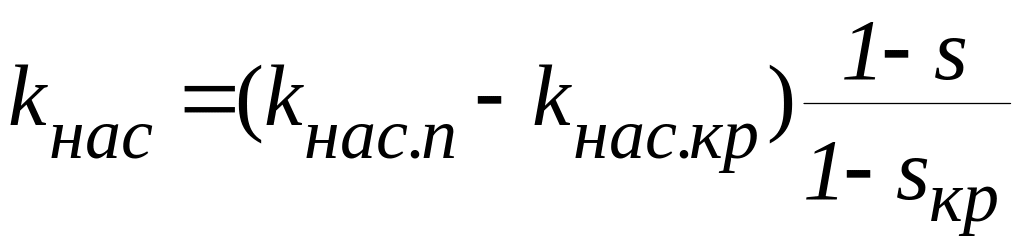где
приведенный ток ротора
из. п. 9.23 при s=1;
из п. 9.23 при
;
из п. 9.10 при s=1,
из п. 9.10 при
.
