Сечения геометрических тел

В стереометрии нередко приходится рассматривать сечения тел различными плоскостями.

Сечением пространственного тела называется фигура, которая получается в пересечении тела с плоскостью (секущей плоскостью).

Простейшие сечения многогранников

• Диагональное сечение – это сечение плоскостью, проходящей через два боковых ребра, не принадлежащих одной грани.

• Сечение плоскостью параллельной основанию.

Обратите внимание, что сечением многогранника является плоский многоугольник.

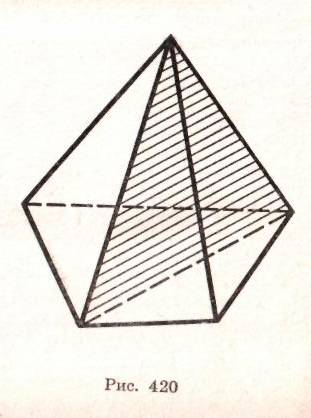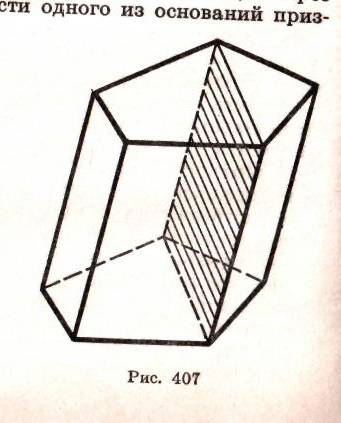З адание. Назовите и опишите свойства указанных сечений.

Задание.

1. По заготовкам постройте:

• Для наклонной пятиугольной призмы – сечение плоскостью параллельной основанию.

• Для прямой четырехугольной призмы – диагональное сечение.

2. Введите обозначения.

3. Опишите особенности построенных сечений (под рисунком).

Усеченная пирамида

Усеченная пирамида  это пирамида, которая получается следующим способом: берется произвольная пирамида, и через точку бокового ребра проводится плоскость, параллельная основанию пирамиды. Данная плоскость разделила пирамиду на две фигуры: пирамиду подобную исходной и многогранник. Полученный многогранник называется усеченной пирамидой. Основаниями усеченной пирамиды служат подобные многоугольники.

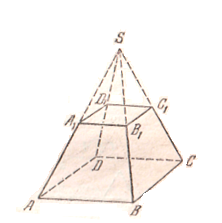
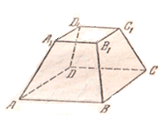
ABCDA₁B₁C₁D₁ – усеченная пирамида

Опишите элементы усеченной пирамиды:

Опишите свойства усеченной пирамиды

Нижнее основание

Перпендикуляр, опущенный из точки верхнего основания на нижнее − называется высотой усеченной пирамиды.

Виды усеченных пирамид.

• Если усеченная пирамида получается из правильной пирамиды, то она называется правильной усеченной пирамидой. Боковые грани правильной усеченной пирамиды являются равными равнобедренными трапециями.

Площадь полной поверхности усеченной пирамиды равна сумме площадей оснований и боковых граней.

S_полн = S_бок + S_{осн 1} + S_{осн 2}

Правильные многогранники

Правильный многогранник – это выпуклый многогранник, у которого все грани – одинаковые правильные многоугольники.

Существует пять типов правильных многогранников.

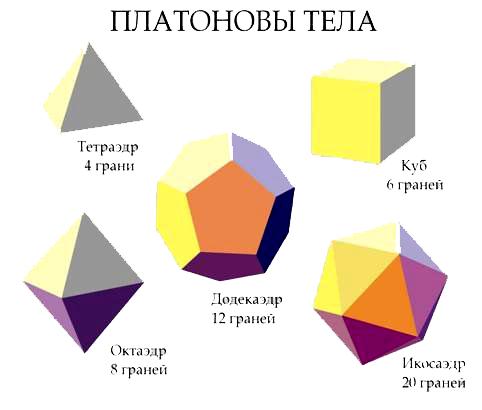
Количественные характеристики правильных многогранников

Многогранник	Вершин	Ребер	Граней
Тетраэдр	4	6	4 треугольника
Куб (гексаэдр)	8	12	6 квадратов
Октаэдр	6	12	8 треугольников
Икосаэдр	12	30	20 треугольников
Додекаэдр	20	30	12 пятиугольников

Для всех выпуклых многогранников выполняется теорема Эйлера: В – Р + Г = 2,

где В – число вершин, Р – число ребер, Г – число граней.

• Проверьте теорему для правильных многогранников!