Экзаменационный билет № 36

1. Отличие Интернет – рекламы от других средств рекламы (радио, тв, газеты)

Параметр	Интернет	Радио	Газета	ТВ
Большая аудитория	+	+\-	+/-	+/-
Международный охват	+	-		+/-
Возможность обращения к целевой группе	+			+/-
Удобство просмотра	+	-	+	+/-
Типа восприятия	Визуально-аккустическое	Аккустическое	визуальное	Визуально-аккустическое
Поток информации	Двунаправленный	Однонаправленный
Подача информации	Динамическая	Динамическая	Статическая	Динамическая
Обращение к публике	Индивидуально/массово	Массово
Стоимость	Низкая	Средняя	Средняя	Высокая

2. Основные понятия интегрального исчисления. Определенный интеграл. Кратные интегралы.

Интеграл функции — аналог суммы последовательности. Неформально говоря, (определённый) интеграл является площадью части графика функции (в пределах интегрирования), то есть площадью криволинейной трапеции.

Процесс нахождения интеграла называется интегрированием.

Согласно основной теореме анализа, интегрирование является операцией, обратной дифференцированию, чем помогает решать дифференциальные уравнения.

Определённый интеграл — аддитивныймонотонныйнормированныйфункционал, заданный на множестве пар, первая компонента которых есть интегрируемаяфункция или функционал, а вторая — область в множестве задания этой функции (функционала).

Пусть определена на . Разобьём на части с несколькими произвольными точками . Тогда говорят, что произведено разбиение отрезка Далее выберем произвольную точку , ,

Определённым интегралом от функции на отрезке называется предел интегральных сумм при стремлении ранга разбиения к нулю , если он существует независимо от разбиения и выбора точек , то есть

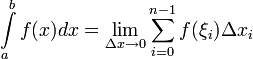
Если существует указанный предел, то функция называется интегрируемой на по Риману.

Обозначения

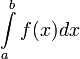
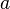•  — нижний предел.

•  — верхний предел.

•  — подынтегральная функция.

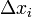•  — длина частичного отрезка.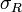

•  — интегральная сумма от функции на соответствующей разбиению .

•  — максимальная длина част. отрезка.

Свойства

Если функция интегрируема по Риману на , то она ограничена на нем.

В математическом анализе кратным или многократным интегралом называют множество интегралов, взятых от переменных. Например:

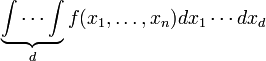
Замечание: кратный интеграл − это определенный интеграл, при его вычислении всегда получается число.