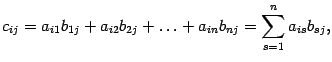- •Экзаменационный билет №1
- •Основные понятия информационных сигналов.
- •Значение информатизации архивного дела на современном этапе. Цели, направления и принципы информатизации архивного дела.
- •Экзаменационный билет № 2
- •Организация информатизации архивного дела на федеральном уровне (планирование, финансирование).
- •2.Аналоговая и цифровая передача данных.
- •Экзаменационный билет № 3
- •Организация информатизации архивного дела на уровне региона (планирование, финансирование).
- •Эффективность передачи и методы ее увеличения.
- •Экзаменационный билет №4
- •1.Структура сети gsm.
- •2.Концепция и Программа информатизации архивного дела в рф.
- •Экзаменационный билет № 5
- •Нормативно – правовая база информатизации архивного дела на современном этапе.
- •Подсистема коммутации.
- •Экзаменационный билет №6
- •Основные итоги информатизации архивного дела во вт. Пол 1980-1990-е годы.
- •Цифровой сигнал.
- •Экзаменационный билет № 7
- •Автоматизированные архивные технологии в области комплектования архива и экспертизы ценности документов.
- •2. Методы и технологии обработки сигналов.
- •Сравнение аналоговой и цифровой обработки сигналов
- •Экзаменационный билет № 8
- •1. Протокол gprs
- •Автоматизированные архивные технологии в области использования документов.
- •Экзаменационный билет № 9
- •Локальные вычислительные сети в архивах.
- •Экзаменационный билет № 10
- •Основные направления использования интернета в архивном деле. Разновидности архивных сайтов.
- •2.Безопасность и быстродействие криптосистемы rsa
- •Экзаменационный билет № 11
- •Применение технологии оцифрования в архивах: основные направления, перспективы, стандарты.
- •Модуляционная схема edge.
- •Экзаменационный билет № 12
- •1 Виды ценных бумаг. Классификация. Характеристика ценных бумаг.
- •Представление изображений в ис. Типы изображений, пикселы, разрешение, размер изображений, цветовые модели, форматы файлов.
- •Экзаменационный билет № 13
- •1. Виды профессиональной деятельности на рынке ценных бумаг.
- •Предварительная обработка изображений – точечные операции: соляризация, линейное контрастирование, препарирование, пороговая обработка.
- •Экзаменационный билет № 14
- •1.Виды графиков, используемые в техническом анализе.
- •Гистограммы и их преобразования. Использование гистограммы в алгоритмах обработки изображений.
- •Использование гистограммы в алгоритмах обработки изображений
- •Экзаменационный билет № 15
- •1.Графические фигуры технического анализа. Фигуры продолжения тренда. Разворотные фигуры
- •2.Представление цвета в изображениях. Цветовые модели.
- •Экзаменационный билет № 16
- •Группы индикаторов технического анализа. Состав и характеристики групп.
- •Методы сжатия изображений: классификация.
- •Экзаменационный билет № 17
- •2.История развития ис и Интернета
- •Правовое регулирование электронных документов.
- •Экзаменационный билет № 18
- •Обеспечение сохранности электронных документов.
- •Экзаменационный билет № 19
- •Топология лвс. Структурирование топологии лвс с помощью повторителей, концентраторов, мостов, коммутаторов, маршрутизаторов и шлюзов.
- •Матрицы. Действия над ними. Обратная матрица.
- •Экзаменационный билет № 20
- •Классификация электронных документов.
- •Экзаменационный билет № 21
- •Управление развитием Интернет: Общество Интернета, Совет по архитектуре, Инженерный совет, Исследовательская группа по развитию интернет – технологий. Ip-протоколы версий 4 и 6.
- •Ip протоколы версий 4 и 6
- •Комплектование и экспертиза ценности электронных документов.
- •Экзаменационный билет № 22
- •Классификация электронных изданий
- •Определение электронной коммерции.
- •Экзаменационный билет № 23
- •Электронный учебник
- •Определение, понятие электронного бизнеса
- •Экзаменационный билет № 24
- •Электронное учебное пособие
- •2.Место системы электронной коммерции в сети Интернет
- •Экзаменационный билет № 25
- •1.Официальные электронные издания.
- •Проблемы, свойственные Интернет бизнесу
- •Экзаменационный билет № 26
- •1.Матрицы. Действия над ними. Обратная матрица.
- •2.Эволюция методов использования Интернет (мало инфы!!!гуглить!!!)
- •Экзаменационный билет № 27
- •Электронные издания в области экономики.
- •Понятие гипертекста.
- •Экзаменационный билет № 28
- •Художественные электронные издания
- •Экзаменационный билет № 29
- •Классификация Web- сайтов и их назначение, особенности
- •Справочные электронные издания
- •Экзаменационный билет № 30
- •Состав и принципы работы поисковых систем
- •Электронные периодические издания. Классификация электронных сми
- •Экзаменационный билет № 31
- •1.Модели поведения посетителей Интернет.
- •Экзаменационный билет № 32
- •Этапы построения сайта
- •Сетевые электронные издания и их разработка.
- •Экзаменационный билет № 33
- •Классификация посетителей Интернет - магазинов.
- •Мультимедийные электронные издания.
- •Экзаменационный билет № 34
- •Этапы построения сайта
- •2.Распространение и хранение электронных изданий.
- •Экзаменационный билет № 35
- •Инструменты Интернет – рекламы, характеристики
- •Линейные пространства. Основные понятия линейных пространств. Линейные пространства в аналитической геометрии.
- •Экзаменационный билет № 36
- •Отличие Интернет – рекламы от других средств рекламы (радио, тв, газеты)
- •Основные понятия интегрального исчисления. Определенный интеграл. Кратные интегралы.
Матрицы. Действия над ними. Обратная матрица.





Произведением
матрицы
![]() размеров
размеров
![]() на
матрицу
на
матрицу
![]() размеров
размеров
![]() называется
матрица
называется
матрица
![]() размеров
размеров
![]() ,
элементы которой вычисляются по формуле
,
элементы которой вычисляются по формуле
|
(14.5) |
где
![]() ,
,
![]() .
.
Во-первых, в этом определении нужно обратить внимание на то, что важен порядок сомножителей, нужно знать, какой сомножитель первый, а какой -- второй.
Во-вторых, нужно отметить, что произведение определено только в том случае, если число столбцов первого сомножителя равно числу строк второго. Если это условие не выполняется, то произведение не определено.
В-третьих, размеры результата умножения определяются следующим образом: число строк результата равно числу строк первого сомножителя, а число столбцов результата равно числу столбцов второго сомножителя.
Правило вычисления элементов произведения можно сформулировать следующим образом.
Для
того, чтобы вычислить элемент произведения,
стоящий в
![]() -ой
строке и
-ой
строке и
![]() -ом
столбце, нужно взять
-ую
строку первого сомножителя и
-ый
столбец второго сомножителя, попарно
перемножить их элементы, стоящие на
одинаковых местах, и результаты сложить.
(Точно так же мы поступаем, когда находим
скалярное произведение двух векторов
по их координатам, см. формулу (14.2).)
-ом
столбце, нужно взять
-ую
строку первого сомножителя и
-ый
столбец второго сомножителя, попарно
перемножить их элементы, стоящие на
одинаковых местах, и результаты сложить.
(Точно так же мы поступаем, когда находим
скалярное произведение двух векторов
по их координатам, см. формулу (14.2).)
Пример
Даны матрицы
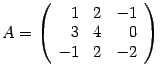 ,
,
 .
Найдите произведения
.
Найдите произведения
![]() и
и
![]() .
.
Решение.
Рассмотрим произведение
.
Число столбцов в первом сомножителе
![]() равно
3, число строк во втором сомножителе
равно
3, число строк во втором сомножителе
![]() тоже
равно 3. Числа совпали, следовательно,
произведение определено.
тоже
равно 3. Числа совпали, следовательно,
произведение определено.
Результатом
умножения будет матрица
,
![]() ,
у которой строк столько, сколько их в
первом сомножителе, то есть 3, а столбцов
столько, сколько их во втором сомножителе,
то есть 2. Итак, матрица
имеет
размеры
,
у которой строк столько, сколько их в
первом сомножителе, то есть 3, а столбцов
столько, сколько их во втором сомножителе,
то есть 2. Итак, матрица
имеет
размеры
![]() .
.
Находим
элемент
![]() .
В его вычислении участвует первая строка
.
В его вычислении участвует первая строка
![]() первого
сомножителя
и
первый столбец
первого
сомножителя
и
первый столбец
 второго
сомножителя
:
второго
сомножителя
:
![]()
Находим
элемент
![]() .
В его вычислении участвует первая строка
первого
сомножителя
и
второй столбец
.
В его вычислении участвует первая строка
первого
сомножителя
и
второй столбец
 второго
сомножителя
:
второго
сомножителя
:
![]()
Все
элементы первой строки матрицы
вычислены.
Находим элемент
![]() .
В его вычислении участвует вторая строка
.
В его вычислении участвует вторая строка
![]() первого
сомножителя
и
первый столбец
второго
сомножителя
:
первого
сомножителя
и
первый столбец
второго
сомножителя
:
![]()
Находим
элемент
![]() .
В его вычислении участвует вторая строка
первого
сомножителя
и
второй столбец
второго
сомножителя
:
.
В его вычислении участвует вторая строка
первого
сомножителя
и
второй столбец
второго
сомножителя
:
![]()
Вычислены все элементы второй строки матрицы . Аналогично находим элементы третьей строки:
![]()
![]()
Итак,
 .
.
Рассмотрим произведение . Число столбцов в первом сомножителе равно 2, число строк во втором сомножителе равно 3. Числа не совпали, следовательно, произведение не определено.
Ответ: ,
произведение
не
определено.
,
произведение
не
определено.

Обра́тная ма́трица — такая матрицаA−1, при умножении на которую, исходная матрица A даёт в результате единичную матрицуE:
![]()
Квадратная матрица обратима тогда и только тогда, когда она невырожденная, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует. Однако возможно обобщить это понятие и ввести псевдообратные матрицы, похожие на обратные по многим свойствам.
![]()
![]() —
транспонированная
матрица алгебраических дополнений;
—
транспонированная
матрица алгебраических дополнений;
Полученная матрица A−1 и будет обратной. Сложность алгоритма зависит от сложности алгоритма расчета определителя Odet и равна O(n²)·Odet.
Иначе говоря, обратная матрица равна единице, делённой на определитель исходной матрицы и умноженной на транспонированную матрицуалгебраических дополнений элементов исходной матрицы.
Транспонированная
матрица —
матрица![]() ,
полученная из исходной матрицы
,
полученная из исходной матрицы
![]() заменой
строк на столбцы.
заменой
строк на столбцы.
------------------------------------------------------------------------------------------