1.2. Методичні вказівки до вивчення методів вимірювання

В результаті вимірювання визначають числове значення вимірюваної величини, рівне відношенню вимірюваної величини до одиниці виміру.

Залежно від конкретних умов, вживаних вимірювальних засобів і прийомів їх використання вимірювання можуть виконуватись різними способами або методами. З точки зору загальних прийомів отримання результатів розрізняють виміри прямі і непрямі.

При прямих вимірах шукана величина визначається безпосередньо показаннями приладу. До прямих вимірювань відносяться вимірювання довжин штангенінструментом, мікрометрами, вимірювання кутів кутомірами та ін.

При непрямих вимірюваннях шукана величина (розмір або відхилення) визначається за результатами прямих вимірювань однієї або декількох величин, пов'язаних з шуканою певною залежністю.

Прикладом непрямих вимірювань можуть служити тригонометричні виміри кутів по двох катетах, по катету і гіпотенузі та ін.

Прямі виміри простіші і відразу призводять до результату виміру, тому вони мають переважне поширення в машинобудуванні. Проте у ряді випадків прямі виміри не можуть бути здійснені, наприклад, при вимірі штангенциркулем відстані між осями отворів або поступаються по точності непрямим вимірам, як це має місце при вимірі кутів кутомірами, погрішності яких в десятки разів перевищують погрішності синусних лінійок.

Кожне вимірювання може робитися абсолютним або відносним методом.

При абсолютному методі увесь вимірюваний розмір визначається безпосередньо за свідченнями приладу.

Відносний метод вимірювання безпосередньо дає тільки відхилення розміру від настановної міри або зразка, по яких прилад був встановлений на нуль. Визначення розміру в цьому випадку робиться підсумовуванням алгебри розміру настановної міри і показань приладу при вимірюванні.

Прилади для відносних вимірювань вимагають додаткової витрати часу для попереднього налаштування приладу по настановній мірі, що істотно знижує продуктивність вимірювань при невеликих партіях деталей, що перевіряються. Зниження продуктивності стає несуттєвим, якщо після налаштування приладом роблять велике число вимірювань.

Прилади для відносних вимірювань, як правило, дозволяють отримати більш високу точність, а при вимірі великих партій деталей - більш високу продуктивність контролю, завдяки зручності відліку відхилень розміру за шкалою приладу.

Крім того, методи виміру діляться на комплексні і диференційовані .

Комплексний метод виміру полягає в зіставленні дійсного контуру об'єкту, що перевіряється, з його граничними контурами, визначуваними величинами і розташуванням полів допусків окремих елементів цього об'єкту. Комплексний метод вимірювання забезпечує перевірку накопичених погрішностей взаємозв'язаних елементів об'єкту, обмежених сумарним допуском. Цей метод вимірювання є найбільш надійним з точки зору забезпечення взаємозамінності і зазвичай здійснюється прохідними калібрами, сконструйованими за принципом подібності.

Прикладом комплексного методу виміру може служити перевірка різі прохідною різьбовою пробкою.

Диференційований метод виміру зводиться до незалежної перевірки кожного елементу окремо. Цей метод не може безпосередньо гарантувати взаємозамінності виробів. Наприклад, при диференційованій перевірці середнього діаметру, кроку і половини вугілля профілю різі необхідно додатково підрахувати приведений середній діаметр різі, що включає відхилення перерахованих вище за елементи різі, і переконатися, що він знаходиться в заданих межах.

Комплексний метод виміру застосовується переважно при перевірці виробів, а диференційований метод - при перевірці інструментів і при виявленні причин розмірного браку виробів.

При контролі виробів граничними калібрами зазвичай поєднуються комплексні і диференційовані методи вимірювань.

Кожен з перелічених вище методів виміру може здійснюватися контактним або безконтактним способом.

Контактний метод виміру здійснюється шляхом безпосереднього зіткнення вимірювальних поверхонь приладу або інструменту з поверхнею контрольованого об'єкту.

Безконтактний метод виміру характеризується відсутністю вимірювального контакту з об'єктом (наприклад, при проекційному або пневматичному методі виміру), що перевіряється.

+++++++++++++++30

Лабораторна робота № 5

Вимірювання геометричних параметрів виробів непрямими методами.

Мета роботи – освоїти метод вимірювання непрямими методами

Завдання – виміряти радіус сегментної шпонки фіксації на інструментальному мікроскопі.

Об’єкт вимірювання – сегментна шпонка фіксації крильчатки підкачувальної системи БЦН.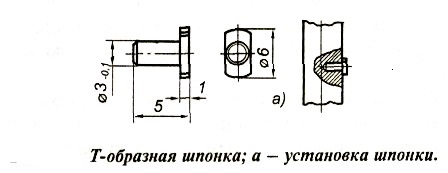

Надійне балансування високооборотної крильчатки вимагає точного її центрування на валу електродвигуна, яке забезпечується точністю насадки із застосуванням сегментної шпонки, параметри точності якої повинні відповідати нормативним вимогам.

Засоби вимірювань – інструментальний мікроскоп БМИ(ММИ) (див. Лабораторна робота № )

У багатьох випадках величина, яку треба визначити, не може бути виміряна безпосередньо, оскільки вимір виявляється незручним, а іноді просто неможливим. В той же час ця величина залежить від ряду незалежних між собою величин і виражається деякою функцією, в яку ці величини входять як аргументи.

Для визначення такої величини вимагається заздалегідь досліджувати, випробувати або виміряти величини, що входять в якості аргументів у вказану функцію. І тільки після цього, підставляючи отримані числові значення виміряних величин і вирішуючи вираження відносно функції, ми отримаємо її чисельне значення.

Такий метод дослідження або вимірювання називається в метрології непрямим методом.

Формула квадратичної помилки для функції в загальному вигляді виходить при її розкладанні в ряд Тейлора

(10)

Формула (10) широко використовується в техніці. З її допомогою можна легко і просто обчислювати помилки величин, отриманих непрямим методом вимірювання.

По формулі (10) отримують квадратичну помилку, вичислену по ряду результатів повторних вимірювань однієї і тієї ж величини. Квадратична помилка характеризує собою міру однорідності числових значень результатів і, отже, як би точність цього ряду. Для середнього арифметичного X ряду результатів квадратична погрішність буде іншою.

Розглядатимемо середнє арифметичне X як функцію декількох змінних X₁, Х₂, . Х_n

Увесь ряд в цілому і кожен його член окремо можуть бути охарактеризовані квадратичною помилкою σх.

Тоді для обчислення середньої квадратичної помилки середнього арифметичного σх можна скористатися формулою (10) і записати, що

Приватні похідні вирази середнього арифметичного будуть

Підставляючи їх значення в попереднє вираження, отримаємо

(11)

З формули (11) виходить, що зі збільшенням числа повторних вимірювань середня квадратична помилка, що характеризує точність середнього арифметичного X, зменшуватиметься, тобто σх = 0 при n→∞.

Таким чином, середня квадратична погрішність середнього арифметичного Z ряду результатів вимірювань непрямим методом визначається по формулі

(12)

де - окремі похідні функції Z, числові значення яких обчислюють, підставляючи середні арифметичні значення x, y, t,..., визначувані за результатами повторних вимірювань по формулах

(13)

де x_i, y_i, t_i,... - числові результати повторних вимірювань; n - число вимірювань; σx, σy, σt,... - середні квадратичні помилки середнього арифметичного величин x, y, t,..., визначувані по формулі (11);

де σx, σy, σt - середні квадратичні відхилення вимірюваних величин

(14)

Вичислену по формулі (12) похибку непрямого методу вимірювання порівнюють з граничною погрішністю показань відлікового приладу при прямому методі вимірювання.