Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Cаратовский государственный технический университет Измерение длины световой волны с помощью дифракционной решетки

Методические указания

к выполнению лабораторной работы по физике

для студентов всех специальностей

всех форм обучения

Электронное издание локального распространения

Одобрено

редакционно-издательским советом

Саратовского государственного

технического университета

САРАТОВ - 2011

Все права на размножение и распространение в любой форме остаются за разработчиком.

Нелегальное копирование и использование данного продукта запрещено.

Составители – В.Б. Сиволобов, Л.Я. Рихтер.

Под редакцией В.В. Сысоева.

Рецензент – И.В. Беляев

410054, Саратов, ул. Политехническая 77,

Научно-техническая библиотека СГТУ,

тел. 52-63-81, 52-56-01

http://lib.sstu.ru

Регистрационный

номер

© Саратовский государственный

технический университет 2011 г.

ЦЕЛЬ РАБОТЫ: определить длину световой волны с помощью дифракционной решетки

Основные понятия

Дифракцией света называется явление отступления от законов прямолинейного распространения света, обусловленное его волновой природой. Дифракция приводит, в частности, к огибанию световыми волнами препятствий и проникновению света в область геометрической тени. Особенно заметно дифракция проявляется, когда размеры препятствий соизмеримы с длиной световой волны. В результате дифракции за препятствием наблюдается дифракционная картина – светлые и темные полосы, кольца и т.д., в зависимости от формы препятствия.

Дифракционная картина является результатом сложения (интерференции) так называемых вторичных световых волн. Понятие о вторичных световых волнах было введено Гюйгенсом. Затем его идеи были развиты Френелем, который учел сложение вторичных световых волн.

Назовем фронтом световой волны поверхность в пространстве, до которой в данный момент дошли световые колебания в одной фазе. Световые лучи в изотропной среде всегда перпендикулярны фронту световой волны. Например, точечный источник света создает сферический фронт волны, а лучи расходятся по радиусам.

Согласно принципу Гюйгенса каждую точку фронта световой волны можно рассматривать как самостоятельный источник сферических световых волн. Эти волны называются вторичными. В любой следующий момент времени фронт волны можно построить как поверхность, огибающую все вторичные волны.

Вторичные волны складываются друг с другом и могут в одних точках пространства взаимно усилить друг друга, а в других – взаимно ослабить или совсем погасить.

Принцип Гюйгенса – Френеля формулируется следующим образом: амплитуда световой волны в любой точке пространства определяется сложением вторичных волн, которые приходят в эту точку от всех отдельных частей фронта световой волны.

Дифракция на узкой щели

Воспользуемся принципом Гюйгенса – Френеля в частном случае дифракции на одной узкой щели. Пусть параллельный пучок лучей падает нормально на непрозрачный экран, в котором имеется щель. Параллельному пучку лучей соответствует плоский фронт световой волны.

Согласно принципу Гюйгенса каждая точка фронта волны в щели является источником вторичных сферических волн и посылает лучи во всех возможных направлениях (Рис. 1a). Поставим на пути лучей собирающую линзу и в ее фокальной плоскости поместим экран (Рис. 1b). В каждой точке этого экрана будут складываться вторичные волны от щели, прошедшие линзу, и на экране возникает дифракционная картина.

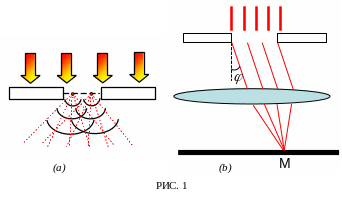
Вторичные волны падают на линзу под всевозможными углами. Выделим лучи, составляющие произвольный угол φ с первоначальным направлением. Линза соберет эти лучи в определенной точке М фокальной плоскости и все эти лучи в данной точке проинтерферируют.

Ч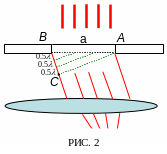 тобы определить результат интерференции воспользуемся методом зон Френеля. Зонами Френеля называют такие участки фронта первичной волны, что вторичные волны от них, складываясь, взаимно гасят друг друга.

Разобьем фронт световой волны в щели на зоны Френеля, согласно Рис. 2. Пусть а – ширина щели, из которой выходит пучок света. Опустим из точки А перпендикуляр АС на крайний луч выделенного пучка. Разделим мысленно линию ВС = аsinφ на ряд отрезков длиной . Проводя из концов этих отрезков линии, параллельные АС, до их пересечения с АВ, мы разобьем фронт волны в щели на ряд полосок одинаковой ширины 1,2,3 и т.д. Эти полоски и являются зонами Френеля.

Совместное действие вторичных волн от двух соседних зон Френеля в точке М приводит к их взаимному гашению, так как волны от соответствующих участков соседних зон (например, от крайних левых, средних и т.д.) приходят в точку М со сдвигом на . Следовательно, если данному углу наклона φ соответствует четное число зон Френеля, то в точке М, в которой соберутся эти лучи, наблюдается минимум интенсивности. Если число зон окажется нечетным, то одна зона останется некомпенсированной, и в точке М наблюдается максимум интенсивности.

В большинстве случаев число зон Френеля не будет целым числом. Для таких углов наблюдается некоторая промежуточная интенсивность.

Выразим условие максимума и минимума интенсивности в общем виде. Из Рис. 2 видно, что число зон Френеля равно

.

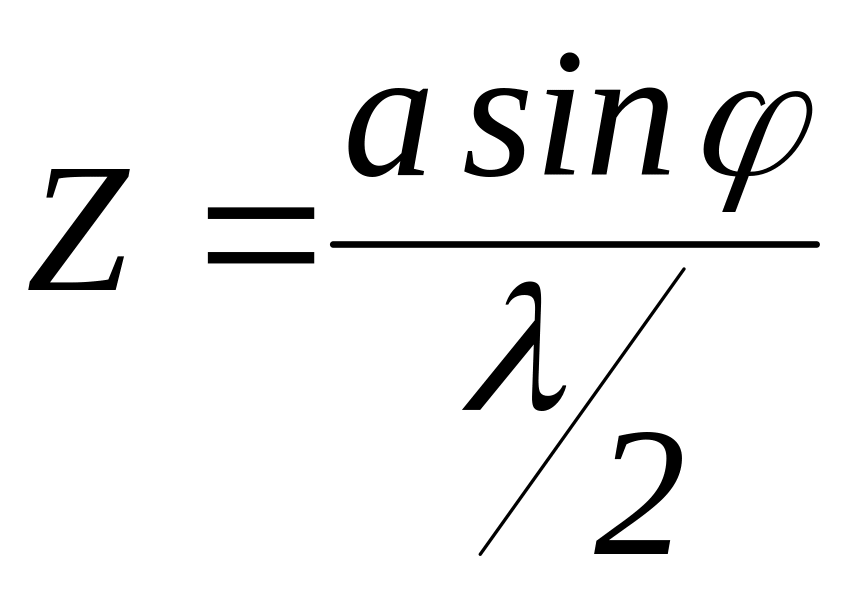Причем число зон может быть как целым, так и дробным.

В точках максимума число Z должно быть целым нечетным, а в точках минимума – целым четным. Возьмем целое число, не равное нулю k=1,2,3,… Любое число 2k будет четным, а (2k+1) – нечетным числом. 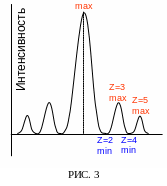Тогда в точках максимума

,

откуда

.

В точках минимума

,

откуда

.

В центре экрана, которому соответствует угол φ=0, наблюдается центральный максимум, так как все вторичные волны приходят в центр в одинаковой фазе.

В целом дифракционная картина представляет собой центральную светлую полосу, параллельную щели, интенсивность которой убывает к краям, а по обе стороны расположены чередующиеся темные и светлые полосы. Распределение интенсивности вдоль экрана изображено на Рис. 3.