Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Саратовский государственный технический университет

Исследование процессов в последовательном lcr контуре

Методические указания к выполнению

лабораторной работы по физике

для студентов всех специальностей

всех форм обучения

Электронное издание локального распространения

Одобрено

редакционно-издательским советом

Саратовского государственного

технического университета

Саратов 2006

Все права на размножение и распространение в любой форме остаются за разработчиком.

Нелегальное копирование и использование данного продукта запрещено.

Составитель - Никишин Евгений Леонардович.

Под редакцией - Зюрюкина Юрия Анатольевича.

Рецензент - Павлова Мария Валентиновна

410054, Саратов, ул. Политехническая 77,

Научно-техническая библиотека СГТУ,

тел. 52-63-81, 52-56-01

http: // lib.sstu.ru

Регистрационный

номер 060545Э

© Саратовский государственный

технический университет 2006 г.

Цель работы: изучение процессов свободных и вынужденных колебаний в последовательном lcr контуре. Электромагнитные колебания

Процесс превращения энергии в колебательном контуре без потерь. Резонансная частота колебаний. Для получения электромагнитных колебаний нужно иметь цепь, в которой энергия электрического поля могла бы превращаться в энергию магнитного поля и обратно. Такую цепь называют колебательным контуром.

Поскольку магнитное поле сосредоточено в соленоиде, а электрическое поле – в конденсаторе, то простейший колебательный контур состоит из соленоида с индуктивностью L и конденсатора с емкостью C. Активное сопротивление проводников, из которых выполнен колебательный контур, должно быть достаточно малым, иначе электромагнитные колебания в контуре не возникнут.

Рассмотрим подробнее, как происходят электромагнитные колебания в такой цепи. Зарядим конденсатор емкостью C до некоторого напряжения U_M и соединим его с катушкой, индуктивность которой L. На рис.1,а показан момент, когда разрядка конденсатора только начинается. В этот момент в конденсаторе имеется электрическое поле, а магнитного поля в катушке еще нет, поэтому вся избыточная энергия контура является электрической и выражается формулой:

E_эл = C U²_м/2 .

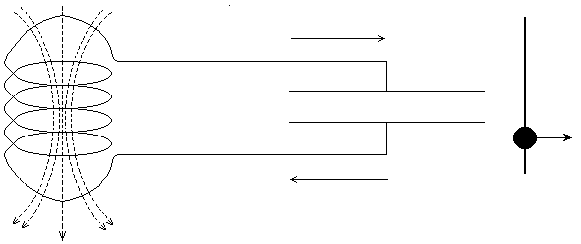
Когда заряды устремляются из конденсатора в катушку, то в ней создаётся э.д.с. самоиндукции, которая тормозит нарастание тока, но прекратить его не может. Ток нарастает до тех пор, пока конденсатор не разрядится полностью. В этот момент (рис.1б) ток в цепи достигает максимальной величины I_м, а вся избыточная энергия контура превращается в энергию магнитного поля катушки и выражается формулой:

Е_м = L I²_м /2.

Е сли активное сопротивление R настолько мало, что потерей энергии на нагревание проводников можно пренебречь, то Е_м будет равно Е_эл. Таким образом, в предельном случае при R = 0, т.е. при собственных колебаниях в контуре, справедлива формула:

(1)

В следующий момент магнитное поле в катушке начинает ослабевать и в ней наводится э.д.с. самоиндукции, поддерживающая прежнее направление тока, вследствие чего происходит перезарядка конденсатора, т.е. превращение магнитной энергии в электрическую.

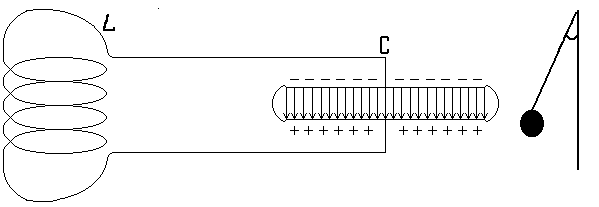
Когда магнитное поле в катушке исчезнет, то конденсатор опять начнёт разряжаться (рис.1в) и в контуре возникает ток обратного направления, пока вся электрическая энергия снова не перейдёт в магнитную (рис.1г). После этого за счёт действия э.д.с. самоиндукции конденсатор опять перезаряжается и достигает состояние, показанное на рис. 1а.

а )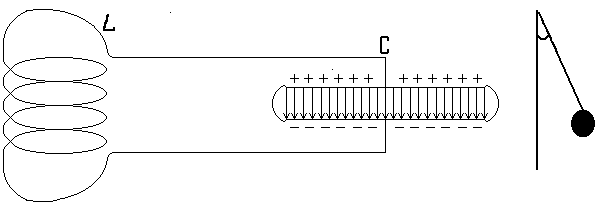

б )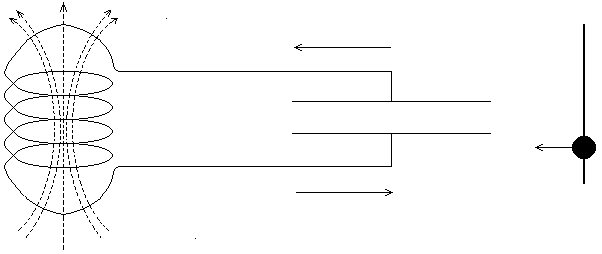

в)

г)

рис.1 Схема процесса электромагнитных колебаний в контуре, состоящем из ёмкости и индуктивности. Буквами а, б, в и г отмечены состояния колебательной системы через каждую четверть периода. Справа для сравнения показаны сходные положения колеблющегося в поле тяготения земли виртуального маятника

Итак, полное колебание в контуре закончено, и далее весь описанный цикл повторяется снова и снова в том же порядке.

Можно заметить большое сходство электромагнитных колебаний в контуре с механическими колебаниями: энергию электрического поля конденсатора можно сопоставить потенциальной энергии математического маятника, а энергию магнитного поля катушки индуктивности – кинетической энергии маятника (рис.1).

Время, затраченное на одно полное колебание, есть период электромагнитных колебаний Т, а их число в единицу времени – частота колебаний ν:

ν = 1/Т.

Как показывает теория, период колебаний в идеальном контуре (при R = 0), т.е. период собственных колебаний, определяется условием равенства реактивных сопротивлений катушки и конденсатора, т.е. формулой:

Х_l = Х_c, или Lω_р = 1/ω_р С. (2)

Частоту ω_р, при которой выполняется это равенство, называют резонансной частотой. При включении контура в цепь именно при такой частоте переменного тока вынужденные колебания в контуре происходят с наибольшей амплитудой. (Попробуйте объяснить, почему при R = 0 амплитуда колебаний должна стать бесконечно большой.)

И з (2) следует, что

Поскольку ω_р = 2π/T, то для периода собственных колебаний в контуре получим:

Т = 2π (4)

Соотношение (4) называют формулой Томсона.

Нетрудно сообразить, что для частоты собственных колебаний в контуре справедлива формула

(5)

Из (5) видно, что при достаточно малых L и C в контуре можно получить колебания высокой частоты, измеряемые миллионами герц и больше.

Поскольку реально контур имеет некоторое активное сопротивление R, то, когда заряженный конденсатор, обладающий энергией E, соединяют с катушкой, при каждом колебании происходит уменьшение энергии E, так как она расходуется на нагревание проводников контура. Это означает, что в реальных случаях свободные колебания в контуре являются затухающими. Очевидно, быстрота затухания колебаний будет возрастать при увеличении R. Ток в контуре носит колебательный характер. График изменения тока изображён на рис.2. Амплитуда колебаний экспоненциально убывает.

р ис.2. Свободные затухающие колебания (δ < ω₀)

Свойства колебательного контура часто характеризуют, указывая его добротность или логарифмический декремент затухания. Введём эти понятия. Амплитуда n-го колебания I_n и амплитуда (n + k)-го колебания I_n+k относятся как

I_n/I_n+k = e^δkT, (6)

где Т – период колебания, равный

Т = 2π/ω,

ω = - циклическая (угловая) частота колебаний,

ω₀ = - собственная частота контура,

t = 1/δ - время релаксации, промежуток времени за который амплитуда уменьшается в e раз,

δ = R/2L - коэффициент, характеризующий затухание колебаний.

Логарифмическим декрементом затухания ν называется величина:

(7)

Если за k колебаний амплитуда колебаний уменьшается в е раз, то θ = 1/k. Логарифмический декремент затухания можно определить, следовательно, как величину, обратную числу периодов, за время которых амплитуда колебаний уменьшается в е раз.

Добротность контура Q определяется с помощью соотношения:

(8)

Чем меньше логарифмический декремент затухания, тем выше добротность контура. При малом затухании ω  ω₀.

(9)

Рассмотрим физический смысл добротности (в случае малых потерь).

Э нергия W₀, запасённая в контуре в начале цикла, равна q₀²/2С, а через период составляет

З а цикл теряется энергия ΔW:

ΔW = W₀(1 – e^-2δТ)  W₀ 2δТ = W₀

Таким образом,

(10)

Т.е. величина добротности определяет, во сколько раз энергия, запасенная в контуре, превосходит среднюю энергию потерь за промежуток времени, в течение которого фаза колебания меняется на 1 радиан.

Если δ = ω₀ – критические условия опыта, то ток в контуре не имеет колебательного характера и является апериодическим (рис.6). Величина сопротивления R_кр, при котором осуществляется критический режим, называется критическим сопротивлением.

( 11)

Т аким образом величина , называемая критическим сопротивлением контура, определяет границу между периодическим и апериодическим процессами в контуре. Заметим, что при заданном значении активного сопротивления, эта граница может быть достигнута изменением индуктивности или ёмкости контура. Последнее обстоятельство используется в данной лабораторной работе – здесь переход к апериодическому режиму достигается включением в контур конденсатора С₃ большей ёмкости (см. схему установки, представленную на рис.7). Время затухания процесса при критическом сопротивлении контура минимально.

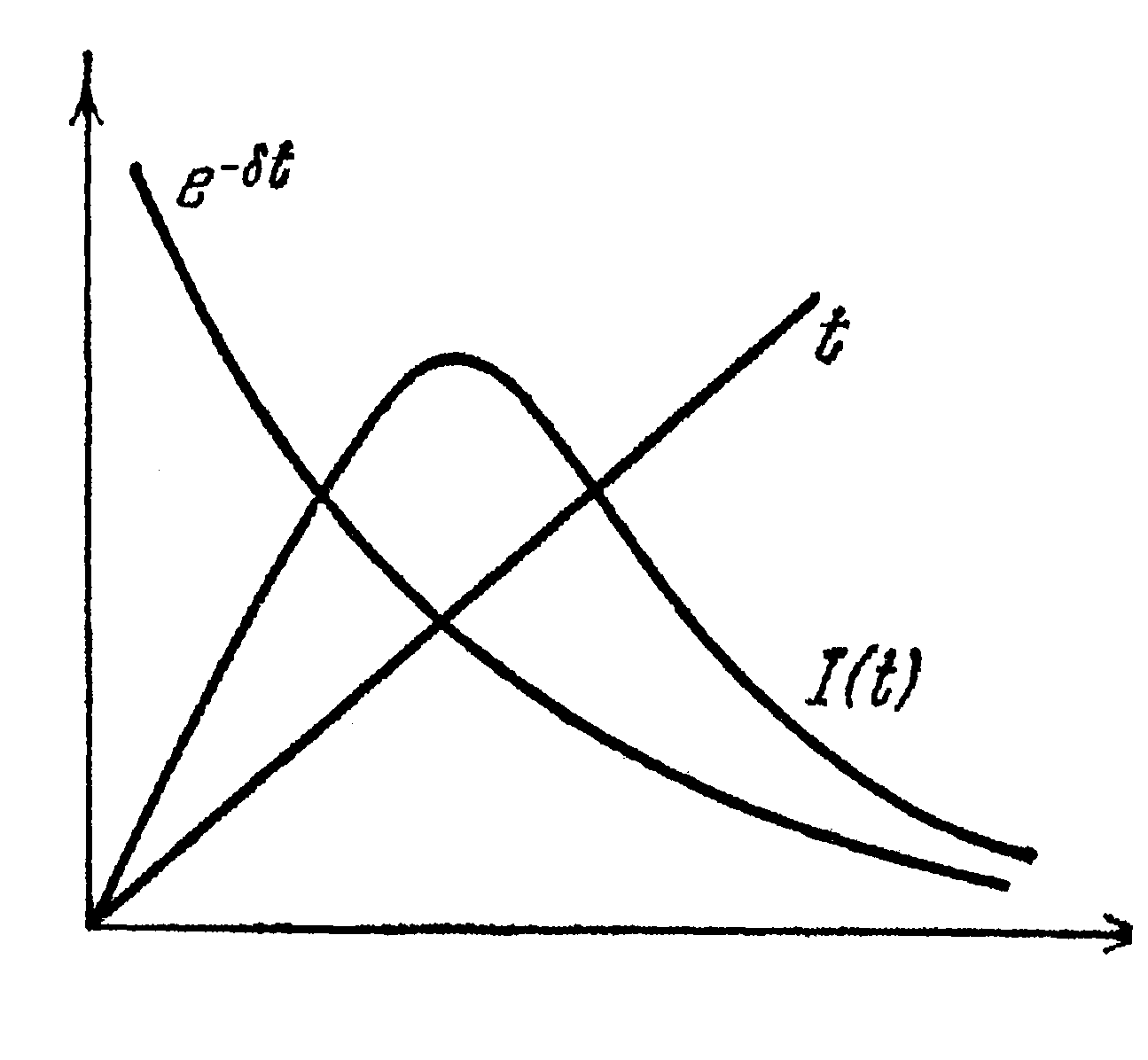
рис.3. Случай критического затухания (δ = ω₀)

Итак, LCR – цепь оправдывает название «колебательный контур» лишь при малых значениях потерь, когда сопротивление контура ниже критического. Рассмотрим далее вынужденные колебания.