
- •Лекция №2. Функции и графики.
- •§1 Понятие функции.
- •§2 График функции. Способы задания функций.
- •§3 Схема исследования функции элементарными способами.
- •§3 Сложная функция.
- •§5 Обратная функция.
- •§6 Элементарные функции.
- •§ 7 Линейная функция.
- •§ 8 Квадратичная функция
- •§ 9 Степенная функция с целым показателем.
- •§ 10 Степенная функция с дробным показателем.
- •§ 11 Показательная функция.
- •§ 12 Логарифмическая функция
- •§ 13 Преобразование графиков
- •Параллельный сдвиг графика
- •Преобразование симметрии.
- •Сжатие и растяжение графиков
- •§ 14 Дробно-линейная функция
- •§ 15 Сложение графиков
§ 14 Дробно-линейная функция
Рассмотрим функцию , c≠0, ad – bc≠0
а≠0
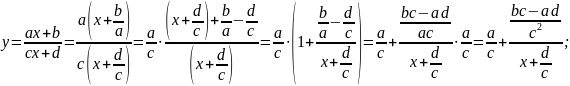
Обозначим
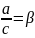 ,
,
 ,
,
 .
Получим: y=
.
Получим: y=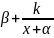 ,
следовательно, график функции
получен из графика функции
,
следовательно, график функции
получен из графика функции
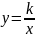 (равнобочная гипербола) с помощью
параллельного сдвига вдоль осей Ох и
Оу.
(равнобочная гипербола) с помощью
параллельного сдвига вдоль осей Ох и
Оу.
Пример:
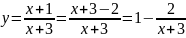
y=
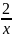
y=
 (сдвиг влево на 3 единицы)
(сдвиг влево на 3 единицы)y=
 (зеркальное отображение относительно
оси Ох)
(зеркальное отображение относительно
оси Ох)y=
 (сдвиг вверх на 1 единицу)
(сдвиг вверх на 1 единицу)
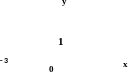
а=0
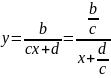 ,
,
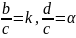 ,
y=
,
y=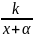 (аналогично)
(аналогично)
Замечание:
Условие
ad
– bc≠0
имеет простой смысл: если ad
– bc
= 0, то числитель и знаменатель в записи
формулы
пропорциональны и при всех значениях
х≠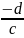 функция сводится к постоянной у=
функция сводится к постоянной у= .
.
§ 15 Сложение графиков
Иногда функция, график которой должен быть построен, представлена как сумма двух простейших функций, графики которых известны.
В этом случае применяют прие графического сложения ординат.
Общий метод построения заключается в том, что предварительно строится два графика для обеих функций, а затем складывают или вычитают ординаты этих кривых при одних и тех же значениях х (удобно в характеристических точках). По полученным точкам строят искомый график и осуществляют проверку в нескольких контрольных точках.
Иногда делают иначе. Строят вначале график одной, более простой функции, затем к нему прибавляют график второй функции, ординаты которого откладывают от соответствующих точек первого графика.
Если надо построить график разности двух функций, то строят сначала график- уменьшаемого, а затем от него откладывают ординаты функции – вычитаемого, взятые с противоположным знаком.
Пример: y= x – sinx
y= x;
От графика функции y= x откладываем ординаты второй функции. Т.к.
 ,
то целесообразно провести две
вспомогательные прямые y=
x+1
и y=
x-1
,
то целесообразно провести две
вспомогательные прямые y=
x+1
и y=
x-1

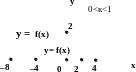
x
x
