
- •Лекция №2. Функции и графики.
- •§1 Понятие функции.
- •§2 График функции. Способы задания функций.
- •§3 Схема исследования функции элементарными способами.
- •§3 Сложная функция.
- •§5 Обратная функция.
- •§6 Элементарные функции.
- •§ 7 Линейная функция.
- •§ 8 Квадратичная функция
- •§ 9 Степенная функция с целым показателем.
- •§ 10 Степенная функция с дробным показателем.
- •§ 11 Показательная функция.
- •§ 12 Логарифмическая функция
- •§ 13 Преобразование графиков
- •Параллельный сдвиг графика
- •Преобразование симметрии.
- •Сжатие и растяжение графиков
- •§ 14 Дробно-линейная функция
- •§ 15 Сложение графиков
§ 7 Линейная функция.
Линейной функцией называется функция вида y=ax+b.
Если b=0, то у=ax: у прямо пропорционально х.
Свойства у=ax:
D(y)=R
y(-x)=-ax=-y(x), следовательно функция нечетная, график симметричен относительно начала координат.
х=0, то у=0, следовательно график проходит через начало координат.
П роведем
через начало координат прямую линию
под углом
к оси Ох так, что tg
=a.
Докажем, что эта прямая и является
графиком функции. Для этого следует
установить два положении: 1) любая точка
этой прямой есть точка графика функции;
2) любая точка графика функции лежит на
построенной прямой.
роведем
через начало координат прямую линию
под углом
к оси Ох так, что tg
=a.
Докажем, что эта прямая и является
графиком функции. Для этого следует
установить два положении: 1) любая точка
этой прямой есть точка графика функции;
2) любая точка графика функции лежит на
построенной прямой.
M0(x0;y0). y0 = tg ∙ x0, tg =
 ,
следовательно,
y0
= ax0,
следовательно точка лежит на графике
функции.
,
следовательно,
y0
= ax0,
следовательно точка лежит на графике
функции.
Пусть для некоторой точки M0(x0;y0) выполняется равенство y0 = ax0, то есть =tg . То есть прямая, соединяющая эту точку с началом координат, наклонена к оси Ох под углом , то есть совпадает с построенной прямой. Ч.т.д.
Итак,
график функции y=ax
– есть прямая, проходящая через начало
координат под углом
(tg )
к оси Ох.
)
к оси Ох.
а – угловой коэффициент прямой.
Если
а>0,
то
 – I
и III
координатная четверть
– I
и III
координатная четверть
a<0,
то
 – II
и IV
координатная четверть
– II
и IV
координатная четверть
а=0 – прямая совпадает с осью Ох.
График функции у= ах+b получается из графика функции у=ах сдвигом на |b| единиц вверх при b>0 или вниз при b<0. Если x=0, то у=b, следовательно, график пересекает ось Оу в точке (0;b).
Вывод: графиком линейной функции является прямая линия, пересекающая ось Оу в точке (0;b) и наклоненная к оси Ох под углом, тангенс которого равен а.
y=ax+b, а – угловой коэффициент, b – начальная ордината.
a<0 функция убывает; а>0 функция возрастает; а=0 функция постоянна.
§ 8 Квадратичная функция
1) y=x2
а) D(y)=R;
б) х=0, то у=0, следовательно график проходит через начало координат;
в) y>0 при x R\{0};
г) y(-x)=y(x), следовательно функция четная, график симметричен относительно оси Оу;
д) при х 0 возрастает, при х 0 убывает
е) х=0 – точка минимума.

2 )
y=аx2
)
y=аx2

3) y
x
y
x

0
x
0
=ax2+bx+c
y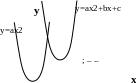 =
a
(x2
+
=
a
(x2
+
 )+c
= a (x2
+
+
)+c
= a (x2
+
+
 )
–
)
– +c= a (x
+
+c= a (x
+
 )2
– –
)2
– –
Итак, график функции y=ax2+bx+c парабола, полученная из графика функции y=ax2
Вывод: 1) Если d<0, то при а>0 график функции весь лежит выше оси абсцисс, и при а<0 ниже оси абсцисс.
2) Если d=0, вершина параболы лежит на оси Ох, если а>0 в верхней полуплоскости, если а<0 в нижней полуплоскости.
3) Если d>0, то график функции пересекает ось Ох в двух точках, при а>0 «ветви» вверх, при а<0 «ветви» вниз.
§ 9 Степенная функция с целым показателем.
у=хn, n N
n
y
=1, у=х – прямая пропорциональность – график прямая
(биссектриса I и III координатных углов)
n=2, у=х2 – парабола
а )
D(y)=R
)
D(y)=R
б) у=0, то х=0, значит график проходит через начало координат.
в) n=2k (четное) у(-х)=у(х), следовательно, функция четная
n=2k+1 (нечетное) у(-х)= –у(х), следовательно, функция нечетная
г)
n=2k
n=2k+1,
x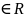 функция возрастает
функция возрастает
При n=3 график называется кубической параболой.
у=xn, n=-1
у =
 ,
общий
случай у
=
,
общий
случай у
=
 – обратная
пропорциональность, m
– коэффициент обратной пропорциональности.
– обратная
пропорциональность, m
– коэффициент обратной пропорциональности.
Свойства
функции у
=
 :
:
D(y)=R\{0};
E(y )=R\{0}, нулей функции нет;
у(-х)=-у(х) – функция нечетная, график симметричен относительно начала координат;
x<0, x1<x2, то , у1>у2, функции убывает Ф
х→ – у→ –0 (с отрицательной стороны)
|
m<0. Если x>0, y<0, еcли x<0, y>0 Самостоятельная работа № 3 Свойства разобрать |
График: равнобочная гипербола.



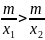 ,
у1>у2,
функция убывает
,
у1>у2,
функция убывает
 ункция
убывает на всей области определения.
ункция
убывает на всей области определения.

