Лекция №2. Функции и графики.

§1 Понятие функции.

Геометрия, механика, физика, различные области науки и техники дают нам множество примеров, когда рассматриваемые переменные величины находятся в зависимости так, что значение одной из величин определяет значение другой. Например, площадь круга полностью определяется величиной его радиуса: S= π R²; скорость точки, движущейся равноускоренно, зависит от ее времени по закону v=v₀+at и т.д. Такого рода зависимости между двумя переменными называются функциональными зависимостями.

♯ Переменная y называется функцией переменной x, если каждому значению x (из некоторой области X изменения x) поставлено в соответствие по определенному закону значение y. При этом x называется независимой переменной (аргументом), а область ее изменения X – областью определения (или существования) функции y. Множество значений, принимаемых y при изменении x, называется областью изменения y.

В принятом определении существенны два момента: 1) в нем указана область изменения X независимой переменной х; 2) в нем требуется наличие определенного правила соответствия между у и х.

Функция у от х выражается в записи: y=f(x).

Буквой f в этом равенстве обозначается именно закон соответствия между у и х.

Схематически это можно изобразить так:

Две функции называются равными (совпадающими), если их области определения совпадают и значения при любых одинаковых значениях аргумента равны.

Пример: f(x)=2; l(x)= 1+ sin²x + cos²x.

§2 График функции. Способы задания функций.

Пусть задана функция f с областью определения D. Рассмотрим координатную плоскость. По оси абсцисс откладываем значения аргумента, а по оси ординат значения функции. Для каждого числа x D можно вычислить y=f(x) и построить точку М(x; f(x)). Множество всех таких точек образует кривую, называемую графиком функции f в заданной системе координат.

♯ Графиком функции f называется множество точек плоскости с координатами (x; f(x)), где х пробегает область определения функции f.

Способы задания функции:

1. Запись функциональной зависимости в виде формулы (функция задана аналитическим выражением). Пример: S= π R²

Область допустимых значений аналитического выражения π R² – все значения R; область определения функции, определенной данным выражением, есть 0<R< .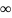

Если функция задана аналитическим выражением относительно аргумента x и область определения не указана, то подразумевают, что область определения совпадает с ОДЗ задающего ее выражения.

2. Табличный способ – для избранных значений аргумента x, обычно отстоящих друг от друга на некоторую постоянную величину – шаг таблицы, указываются соответствующие значения y (с определенной степенью точности).

3. Графический способ

§3 Схема исследования функции элементарными способами.

Основные определения:

1. Функция f(x), область определения которой симметрична относительно начала отсчета О, называется четной, если для из ее области определения выполняется равенство f(-x)= f(x).

График четной функции симметричен относительно оси Оу. Обратное также верно.

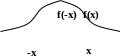
2. Функция f(x), область определения которой симметрична относительно начала отсчета О, называется ytчетной, если для из ее области определения выполняется равенство f(-x)=- f(x).

График нечетной функции симметричен относительно начала координат. Обратное также верно.

3. Нулем (корнем) функции f(x) называется такое значение аргументах, при котором функция обращается в нуль. Графически нули функции – это точки пересечения графика с осью Ох.

4. Функция называется возрастающей в некотором промежутке, лежащем в ее области определения, если для любых двух значений х₁, х₂ из этого промежутка из неравенства х₁< х₂ следует f(х₁)< f(х₂) (большим значениям аргумента соответствуют большие значения функции). Если из неравенства х₁< х₂ следует лишь f(х₁) f(х₂), то функция называется неубывающей.

5. Функция называется убывающей в некотором промежутке, лежащем в ее области определения, если для любых двух значений х₁, х₂ из этого промежутка из неравенства х₁< х₂ следует f(х₁)> f(х₂) (большим значениям аргумента соответствуют меньшее значения функции). Если из неравенства х₁< х₂ следует лишь f(х₁) f(х₂), то функция называется невозрастающей.

Пример:

f(-x)

f(-x)

f(-x)

y=|x|+x; y=

1. х ₁< х₂ 2) х₁< х₂

f(х₁)=f(х₂) f(х₁)< f(х₂)

Итак, функция y=|x|+x неубывающая на всей числовой оси.

6. Т очка х₀ называется точкой максимума (минимума) функции y= f(x), если функция определена в самой этой точке и в некоторой окрестности точки x₀ выполняется неравенство: f(х₀) f(х) (для максимума) f(х₀) f(х) (для минимума).

x_{0 ,} x₂ – точки максимума, x₁, x₃ –точки минимума.

Точки максимума, минимума – точки экстремума.

Максимум функции – ее наибольшее значение по сравнению с «соседними» точками слева и справа, но не обязательно с отдаленными точками.

7. П

   y=0 – асимптота

   рямая линия называется асимптотой графика функции, если график функции неограниченно сближается с этой прямой при удалении точки графика в бесконечность.

Схема

1. Область определения.

2. Нули функции.

3. Промежутки знакопостоянства.

4. Четность, нечетность функции.

5. Промежутки монотонности.

6. Точки экстремума, точки максимума и минимума функции.

7. Асимптоты.

Пример:

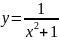
1. D(f)= R

2. f(х)=0

=0 корней нет, следовательно график функции не пересекает ось Ox.

3. f(х)>0, следовательно график расположен выше оси Ox.

4. f(-х)= = f(x), следовательно функция четная, график расположен выше оси Oy

5. а) х ;0). х₁< х₂ f(х₁)= , f(х₂)=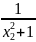 , 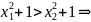f(х₁)< f(х₂)⇒ при х ;0) функция возрастает;

б) х ; ). х₃< х₄ f(х₃)= , f(х₄)= , f(х₃)> f(х₄)⇒ при х ; ). функция убывает;

6. х=0 – точка максимума (возрастание сменяется убыванием)

у(0)=1 – точка максимума функции.

7. Пусть х→ + у→ 0

Пусть х→ – у→ 0