2. Метод Зейделя.

Одним из самых распространенных итерационных методов, отличающихся простотой и легкостью программирования является метод Зейделя. Дана система линейных уравнений (5)

a₁₁x₁+a ₁₂ x₂+ …+ a₁₃x₃ =b₁

a₂₁x₁+a ₂₂ x₂+ …+ a₂₃x₃ =b₂ (5)

a₃₁x₁+a ₃₂ x₂+ …+ a₃₃x₃ =b₃

Р исунок 1- Блок-схема метода итераций

Предположим, что диагональные элементы a_11, a ₂₂ ,a₃₃ отличны от нуля. Выразим неизвестные x_1, x₂, x₃ соответственно из первого, второго и третьего уравнений системы (5)

x₁= (6)

x₂= (7)

x₃= (8)

Зададим некоторые начальные (нулевые )приближения значений неизвестных: х₁= x⁰₁ , х₂=x⁰₂ , х₃= x⁰₃ . Подставляя эти значения в правую часть выражения (6), получаем новое (первое ) приближение для х₁:

x₁¹=

Используя значение для х₁ и приближение x⁰₃ для х₃ находим из (7) первое приближение для х₂:

х¹₂=

И наконец, используя вычисленные значения x₁=x¹₁ и х₂=x¹₂ находим с помощью выражения (8) первое приближение для х₃ :

x¹ ₃=

Используя теперь значения x₁¹, х¹₂, x¹₃ таким же образом провести вторую итерацию в результате которой будут найдены вторые приближения к решению: х₁= x²₁ , х₂=x²₂ , х₃= x²₃ и т.д. Приближение с номером k можно представить в виде:

x₁^k=

х₂ ^k=

x₃ ^k=

Итерационный процесс продолжается до тех пор пока значения x₁^k , х₂ ^k , x₃ ^k не станут близкими с заданной погрешностью с значениями x₁^k-1 , х₂ ^k-1 , x₃ ^k-1.

Итерационный процесс продолжается до тех пор, пока все значения x_i^k не станут близкими к x_i^k-1. Тогда при заданной допустимой погрешности >0 критерий окончания итерационного процесса можно записать в виде

= (9)

Это критерий по абсолютным отклонениям. Можно заменить его критерием по относительным разностям, т.е. условие окончания итерационного процесса записать в виде при |x_i|>>1, тогда (10)

При выполнения условия (9) и (10) итерационный процесс Гаусса-Зейделя называется сходящимся.

Для сходимости итерационного процесса достаточно, чтобы модули диагональных коэффициентов для каждого уравнения системы были не меньше сумм модулей всех остальных коэффициентов:

| a_ii|= , где i=1,2,3,…, n.

Блок-схема алгоритма решения n линейных уравнений методом Гаусса-Зейделя представлена на рисунке 2.

Литература. Осн...7 [ 47-51 ], доп. 26 [133-140]

Контрольные вопросы и задачи

1. При каких условиях итерационный процесс Гаусса-Зейделя называется сходящимся?

2. Опишите алгоритм метода Зейделя , итераций ?

3. Назовите формулы окончания итерационного процесса ?

4. Какой процесс называется сходящимся?

Лекция 8.

Тема лекции : Методы решения линейных уравнений состояния электрической систем. Метод Ньютона .Условия сходимости..

Конспект лекции

1. Метод Ньютона . Многие практические задачи сводятся к решению системы нелинейных уравнений. Пусть для вычисления неизвестных x₁, х₂, ..., х_п тре­буется решить систему п нелинейных уравнений

F ₁(x₁, х₂,, ..., x_n) = 0,

……………………. (1)

F_n(x₁, x₂ , ..., x_n) = 0.

В отличие от систем линейных уравнений не сущест­вует прямых методов решения нелинейных систем обще­го вида. Лишь в отдельных случаях систему (1) можно решить непосредственно. Например, для случая двух уравнений иногда удается выразить одно неизвестное через другое и таким образом свести задачу к решению одного нелинейного уравнения относительно одного не­известного.

Для решения систем нелинейных уравнений обычно используются итерационные методы. Ниже будут рассмот­рен метод Ньютона.

Рисунок 2 – Блок-схема метода Гаусса — Зейделя.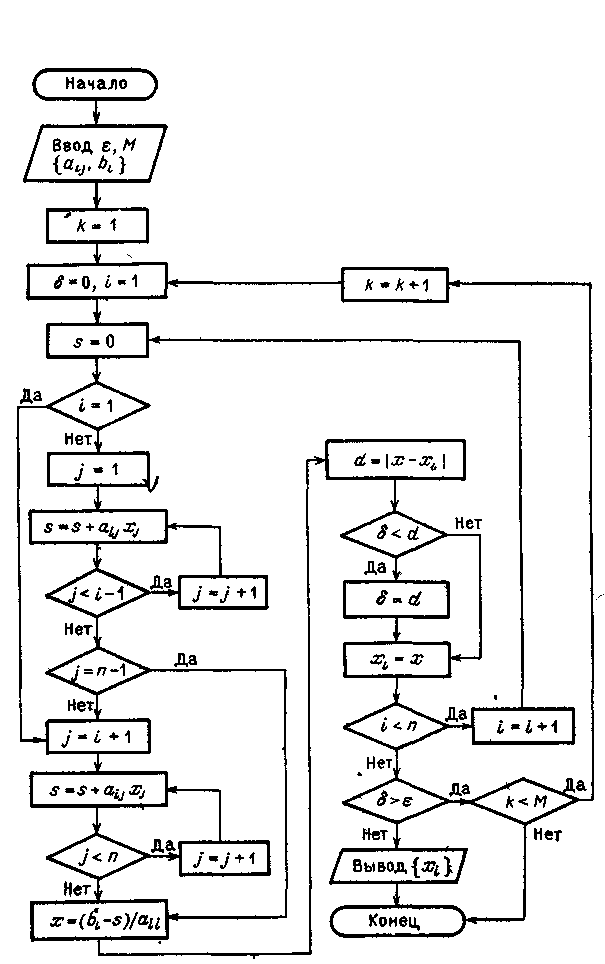

Метод Ньютона. Этот метод обладает гораздо более быстрой сходимостью, чем метод простой итерации. В слу­чае одного уравнения F(x) = 0 алгоритм метода Ньютона был легко получен путем записи уравнения касательной к кривой у = F (х). В основе метода Ньютона для системы уравнений лежит использование разложения функций F_i(x_t, х₂, ..., х_п) в ряд Тейлора, причем члены, содержа­щие вторые (и более высоких порядков) производные, от­брасываются.

Пусть приближенные значения неизвестных системы (1) (например, полученные на предыдущей итерации) равны соответственно a₁, а₂, ,.., а_п. Задача состоит в на­хождении приращений (поправок) к этим значениям x_t, х₂, ..., х_n благодаря которым решение системы (1) запишется в виде

x₁ = a₁ + х₁, х₂ = а₂ +х₂, ... , х_п = а_п + х_п. (2)

Проведем разложение левых частей уравнений (1) с учетом (2) в ряд Тейлора, ограничиваясь лишь линейными членами относительно приращений:

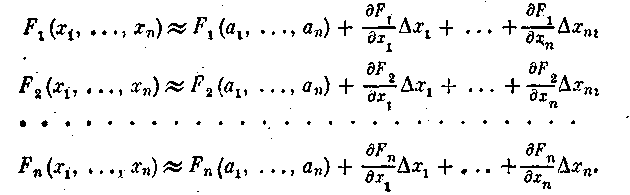
Поскольку в соответствии с (1) левые части этих выражений должны обращаться в нуль, то приравняем нулю, и правые части. Получим следующую систему ли­нейных алгебраических уравнений относительно приращений (3):

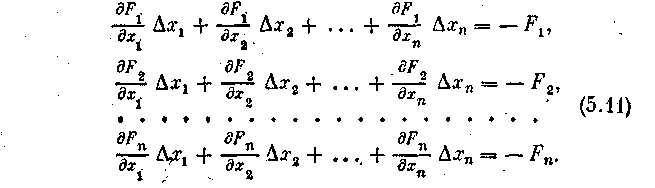
(3)

Значения F₁ F₂, . .., F_n и их производные вычисляются при x₁ = a₁, x₂ = а₂, ..., х_п = a_n.

Определителем системы (3) является якобиан

Д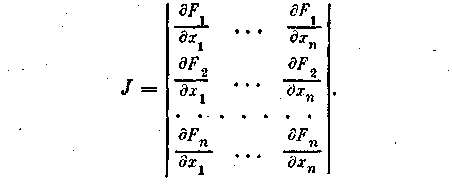 ля существования единственного решения системы (3) он должен быть отличным от нуля на каждой ите­рации. Таким образом, итерационный процесс, решения систе­мы уравнений (1) методом Ньютона состоит в опреде­лении приращений x₁, x₂, ..., х_n к значениям неиз­вестных на каждой итерации. Счет прекращается, если все приращения становятся малыми по абсолютной величине:

max | х_i [ <. В методе Ньютона также важен удачный выбор начального приближения для обеспечения хорошей сходимости. Сходимость ухудшается с увеличе­нием числа уравнений системы.

В качестве примера рассмотрим использование метода Ньютона для решения системы двух уравнений

F₁(x, y) = 0, (4)

F₂(х, у) = 0.

Пусть приближенные значения неизвестных равны a, b. Предположим, что якобиан системы (4) при х = а, у = b отличен от пуля, т. е.

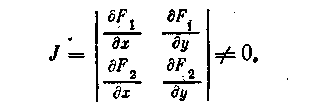
Тогда следующие приближения неизвестных можно за­писать в виде

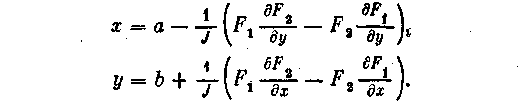
Величины, стоящие в правой части, вычисляются при х = а, у = b.

Блок-схема метода Ньютона для решения системы из двух уравнений изображена на рис. 2. В качестве исходных данных задаются начальные приближения неизвест­ных а, b, погрешность  и допустимое число итераций М. Если итерации сойдутся, то выводятся значения х и у, в противном случае происходит вывод х, у, М.

Метод Ньютона-Рафсона предполагает возможность относительного изменения шага итерации a:

[xⁿ⁺¹] = [xⁿ] - [f '(xⁿ)]^-1 [f(xⁿ)] aⁿ .

Модифицированный метод Ньютона предполагает замораживание инверсной матрицы производных (инверсного Якобиана) на первом шаге:

[xⁿ⁺¹] = [xⁿ] - [f '(x⁰)]^-1 [f(xⁿ)] .

Но в этом случае наблюдается лишь линейное схождение. Хотя, через несколько итераций, инверсный Якобиан можно обновлять.

Литература Осн. 5[323-329 ] Доп. 26[ 164-168] .

Контрольные вопросы и задачи.

1. Построить блок-схему решения системы уравнений методом Ньютона.

2. Используя метод Ньютона, найти с погрешностью 10^-3 хотя бы один корень системы уравнений: a) tg (0.55x +0.1) = x³; x³ - 0.2х² + 0.5х +1.5 = 0.

3. С помощью метода простой итерации найти с погрешностью 10^-3 хотя бы один корень уравнений: а) 5х — 8 In х = 8; б) x² = sin х.

4. Расскажите методику нахождения корней системы нелинейных уравнений?

5. Формула метода Ньютона-Рафсона?

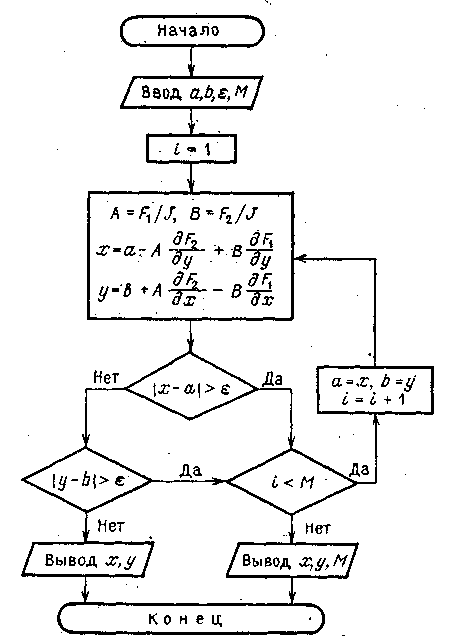
Рисунок 2 –Блок-схема метода Ньютона для системы из двух уравнений

Лекция 9.

Тема лекции : Понятие собственного вектора и собственного значения матрицы

Конспект лекции.

1. Основные понятия. Большое число научно-техни­ческих задач, а также некоторые исследования в области вычислительной математики требуют нахождения соб­ственных значений и собственных векторов матриц. Вве­дем некоторые определения, необходимые для изложения материала данного параграфа.

Рассмотрим квадратную матрицу п-го порядка

(1)

Характеристической матрицей С данной матрицы А называется матрица вида

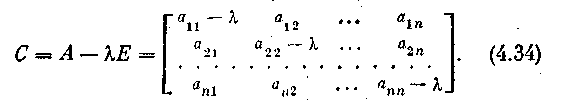
(2)

Здесь  — собственное значение, Е — единичная матрица. Определитель матрицы С является многочленом n-й степени относительно :

detC=c₀ⁿ+ c₁^n-1 +…+ c_n-1+c_n (3)

называемым характеристическим многочленом. Корни этого многочлена являются собственными значениями матрицы А.

Вектор X = {x₁, х₂, ..., х_п}, соответствующий некото­рому собственному значению  и удовлетворяющий си­стеме уравнений

АХ = Х, (4)

называется собственным вектором матрицы А.

Поскольку при. умножении собственного вектора на скаляр он остается собственным вектором той же матри­цы, то его можно нормировать. В частности, каждую ко­ординату собственного вектора можно разделить на мак­симальную из них или на длину вектора; в последнем случае получится единичный собственный вектор.

Если перейти к координатной форме записи векто­ра X, то с учетом (3) систему (4) можно записать в виде

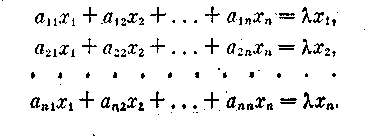
Иногда эту систему уравнений удобно представить в дру­гом виде:

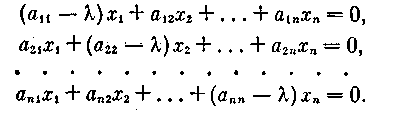
Это уже однородная система п линейных уравнений с п неизвестными. Она имеет ненулевые решения лишь тог­да, когда ее определитель равен нулю: det(A — E)= О, причем решение не единственно, поскольку обычно одно уравнение является -следствием остальных.

На практике обычно при нахождении собственных векторов матрицы одну из его компонент полагают рав­ной некоторому числу, например x₁ = 1. Остальные ком­поненты находятся однозначно из подсистемы линейно независимых уравнений, в которой отброшено уравнение, являющееся следствием остальных. Эта процедура не влияет на результат решения задачи, поскольку, как уже отмечалось, собственные векторы находятся с точностью до постоянного множителя.

Пример. Вычислить собственные числа и собствен­ные векторы матрицы

A=

Решение. Составим характеристический многочлен

| |=(3-)(4-)-2=²-7+10

Найдем корни этого многочлена второй степени:

²-7+10= 0, ₁ = 2, ₂ = 5.

Для нахождения собственных векторов X_1, X₂, соответ­ствующих собственным значениям ₁, ₂, составим систе­мы уравнений типа (4) для каждого из них. При

₁ = 2 получим

[ ] [ ]=[ ]

или в виде системы уравнений :

3x₁ + x₂ = 2x₁

2x₁ +4x₂ = 2x₁

Записывая полученную систему в виде

x₁ + x₂ = 0

x₁ + x₂ = 0

замечаем, что уравнения линейно зависимы (даже совпа­дают). Поэтому оставляем лишь одно из них.

Полагаем x₁ = 1. Тогда х₂ = -x₁ = -1, и собственный вектор, соответствующий собственному значению ₁ = 2, имеет вид X₁ = {1, —1} или X₁ = e₁ — е₂, где e₁, е₂ — еди­ничные орты выбранной базисной системы.

Аналогично находим второй собственный вектор, со­ответствующий собственному значению ₂ =5 Опуская комментарии, получаем

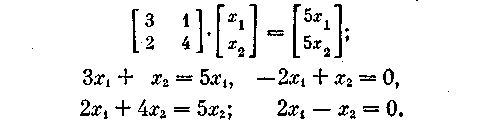
Отсюда x₁ = 1, х₂ = 2, X₂ = e₁ + 2e₂.

Вектор X₁ нормирован; нормируем также вектор Х₂, разделив его компоненты на наибольшую из них. Полу­чим Х₂ = 0,5е₁ + е₂. Можно также привести векторы к единичной длине, разделив их компоненты на значения модулей векторов. В этом случае

Мы рассмотрели простейший пример вычисления соб­ственных значений и собственных векторов для матрицы второго порядка. Нетрудно также провести подобное ре­шение задачи для матрицы третьего порядка и для неко­торых весьма специальных случаев.

В общем случае, особенно для матриц высокого по­рядка, задача о нахождении их собственных значений и собственных векторов, называемая полной проблемой соб­ственных значений, значительно более сложная.

На первый взгляд может показаться, что вопрос сво­дится к вычислению корней многочлена (3). Однако здесь задача осложнена тем, что среди собственных зна­чений часто встречаются кратные. И кроме того, для произвольной матрицы непросто вычислить сами коэффи­циенты характеристического многочлена.

Отметим некоторые свойства собственных значений для частных типов исходной матрицы.

1. Все собственные значения симметрической матрицы действительны.

2. Если собственные значения матрицы действительны и различны, то соответствующие им собственные векторы ортогональны и образуют базис рассматриваемого пространства. Следовательно, любой вектор в данном пространстве можно выразить через совокупность линейно независимых собственных векторов.

3. Если две матрицы A и В подобны, т. е. они связа­ны соотношением

В = Р ^-1АР, (5)

то их собственные значения совпадают (здесь Р — неко­торая матрица).

Преобразование подобия (5) можно использовать для упрощения исходной матрицы, а задачу о вычисле­нии ее собственных значений свести к аналогичной зада­че для более простой матрицы.

Очевидно, самым лучшим упрощением матрицы (1) было бы приведение ее к треугольному виду

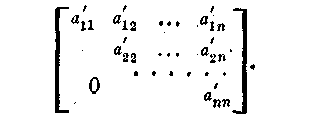
Т огда матрица (2 )также имела бы треугольный вид. Как известно, определитель треугольной матрицы равен произведению ее диагональных элементов, поэтому ха­рактеристический многочлен (3) в этом случае имеет вид

(6)

Собственные значения матрицы, равные корням этого многочлена, можно сразу получить:

(7)

Таким образом, собственные значения треугольной матрицы равны ее диагональным элементам. То же са­мое, естественно, относится и к диагональное матрице, которая является частным случаем треугольной.

Некоторые типы матриц удается привести к треуголь­ному виду с помощью преобразования подобия. В частно­сти, симметрическую матрицу можно привести к диаго­нальному виду. На практике часто используется приве­дение симметрической матрицы к трех диагональному ви­ду. Процедура вычисления собственных значений для полученной матрицы значительно упрощается по срав­нению с задачей для исходной матрицы.

Существует ряд методов, основанных на использова­нии преобразования подобия, позволяющего привести ис­ходную матрицу к более простой структуре. Мы рассмот­рим ниже один из них — метод вращений.

2. Метод вращений. Одним из эффективных методов, позволяющих привести исходную симметричную матрицу n-го порядка к трехдиагональному виду, является метод вращений. Он основан на специально подбираемом вра­щении системы координат в n-мерном пространстве. По­скольку любое вращение можно заменить последователь­ностью элементарных (плоских) вращений, то решение задачи можно разбить на ряд шагов, на каждом из кото­рых осуществляется плоское вращение. Таким образом, на каждом шаге выбираются две оси — i-я и j-я, и пово­рот производится в плоскости, проходящей через эти оси; остальные оси координат на данном шаге неподвижны, Матрица вращения при этом

имеет вид

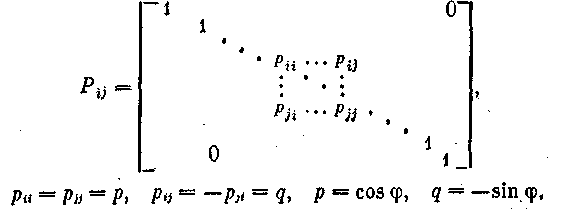
(8)

Здесь мы рассматриваем матрицы с вещественными эле­ментами. В случае комплексных векторов для использо­вания этого метода нужно изменить формулы (8).

Для осуществления преобразования подобия (5) необходимо найти обратную матрицу . Можно пока­зать, что она равна в рассматриваемом случае транспо­нированной матрице , т. е. для получения обратной матрицы достаточно провести зеркальное отражение всех элементов исходной матрицы относительно ее диагонали,

Литература Осн. 7 [58-65] , доп.26 [ 140-154 ]

Контрольные вопросы и задачи.

1. Провести геометрический анализ единственности решения системы трех линейных уравнений с тремя неизвестными в зави­симости от значения определителя.

2. Элементы треугольной матрицы вводятся построчно в па­мять машины. Составить блок-схему вычисления определителя данной матрицы.

3. Используя метод Гаусса, решить следующие системы урав­нений с погрешностью 10-⁴:

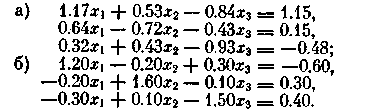
4. Составить блок-схему вычисления обратной матрицы по ме­тоду Гаусса. Блок прямого хода можно считать заданным .

5. С помощью метода прогонки решить систему уравнений

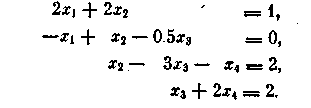
6. Решить методом Гаусса — Зейделя с погрешностью 10-³ си­стемы уравнений:

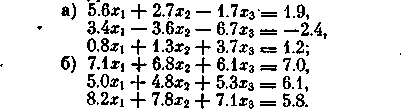
7. Найти собственные значения и собственные векторы матриц

8. Составить алгоритм приведения матрицы четвертого поряд­ка к трехдиагональному виду и решения полной проблемы соб­ственных значений.

9. Составить блок-схему вычисления наибольшего собственно­го значения с помощью итерационного метода.

Лекция 10.

Тема лекции : Линейное программирование. Применение симплекс метода для решения задач энергетики.

Конспект лекции.

Учебно-целевые вопросы:

0. Общие понятия о методах линейного программирования и определения.

1. Пример постановки задачи линейного программирования.

2. Обобщенная и каноническая постановка задачи.

3. Блок-схема эвристического алгоритма реализации задачи линейного программирования.