2. Элементы матриц l и u могут быть записаны на месте элементов матриц а и занесены в те же ячейки памяти (запоминать единичные элементы на главной диагонали матрицы u нет необходимости).

3.Если требуется найти решение для другого вектора b в правой части, то не нужно повторно проводить разложение матриц на треугольные, а достаточно только произвести прямую и обратную подстановки.

4. Для уравнений с транспортированной матрицей А^t X = C решение находится при том же LU-разложении. Анализ таких систем уравнений необходим при расчете чувствительности.

2. Обратная матрица

Определение . Матрица B называется обратной матрицей для квадратной A матрицы если AB=BA=E.

Из определения следует, что обратная матрица В будет квадратной матрицей того же порядка, что и матрица А иначе одно из произведений AB или BA было бы не определено). Обратная матрица для матрицы A обозначается A^-1 Таким образом, если A^-1 существует, то AA^-1 =A^-1A=E.

Из определения обратной матрицы следует, что матрица A является обратной для матрицы A^-1 , то есть (A^-1)^-1 Про матрицы и можно говорить, что они обратны друг другу или взаимно обратны. Если матрица имеет обратную, то |A|<>0 и |A^-1|=|A|^-1 Если квадратная матрица А является невырожденной, то обратная для нее существует и

г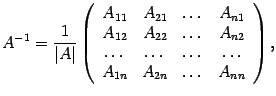 де A_ij алгебраические дополнения к элементам a_ij

Квадратную матрицу A назовем вырожденной или особенной матрицей, если |A|=0и невырожденной или неособенной матрицей, если|A|0

Пример: Найдите обратную матрицу для матрицы

Р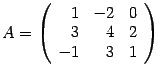 ешение. Находим определитель

Т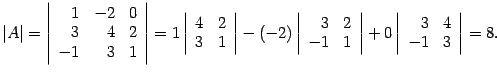 ак как |A|0, то матрица А - невырожденная, и обратная для нее существует

Находим алгебраические дополнения

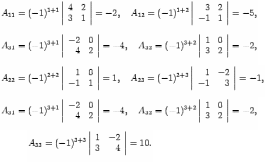
С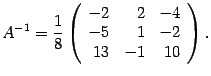 оставляем обратную матрицу, размещая найденные алгебраические дополнения так, чтобы первый индекс соответствовал столбцу, а второй – строке:

Полученная матрица и служит ответом к задаче

Или

Ч тобы избежать ошибок следует делать проверку: вычислить произведение исходной матрицы на итоговую в том или ином порядке. Если в результате получится единичная матрица, то обратная матрица найдена правильно. В противном случае нужно искать ошибку.

3. Обратить матрицу методом разбиения ее на произведение двух треугольных матриц.

Решение состоит из следующих этапов:

1. Представление матрицы А в виде произведения А=Т₁Т₂, где Т₁ и Т₂ – треугольные матрицы

1. Обращение матриц Т₁ и Т₂ , т.е. нахождение матриц Т₁^-1 и Т₂^-1.

2. Нахождение искомой матрицы А^-1 с помощью умножения найденных м атриц:

А^-1= Т₁^-1 * Т₂^-1.

Порядок выполнения.

1.Для отыскания матриц Т₁ и Т₂ используем схему:

Элементы матрицы								
A a11		a12		a13		a14		c1
a21		a22		a23		a24		c2
a31		a32		a33		a34		c3
a41		a42		a43		a44		c4
Т1 и Т2 t11	1	r12		r13		r14		c1`
t21		t22	1	r23		r24		c2`
t31		t32		t33	1	r34		c3`
t41		t42		t43		t44	1	c4`

Столбец  - является контрольным; числа c₁ ,c₂ ,c₃ ,c₄ - строчные суммы;

Элементы схемы находят в следующем порядке:

1. t₁₁=a₁₁; t₂₁=a₂₁; t₃₁=a₃₁ ; t₄₁=a₄₁ ;

2. r₁₂ = ; r₁₃ = ; r₁₄ = ; c₁^ =

Контрольное соотношение : c₁^` = 1+ r₁₂+ r₁₃+ r₁₄

3. t₂₂=a₂₂ - t₂₁r₁₂; t₃₂=a₃₂– t₃₁r₁₂; t₄₂=a₄₂– t₄₁ r₁₂;

4. r₂₃ = ; r₂₄ = ; = ;

Контрольное соотношение

5. t₃₃=a₃₃ – t₃₁r₁₃ – t₃₂r₂₃; t₄₃=a₄₃– t₄₁r₁₃ – t₄₂r₂₃ ; t₄₂=a₄₂– t₄₁ r₁₂;

6. r₃₄ = ; = ;

Контрольное соотношение

7. t₄₄=a₄₄ – t₄₁r₁₄ – t₄₂r₂₄–t₄₃r₃₄;

= ;

Контрольное соотношение

Из найденных элементов составляют матрицы

Пусть дана квадратная матрица (1) и пусть A_ij - обозначает алгебраическое дополнение элемента a_ij .Матрица

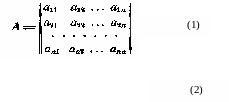
в строчках которой расположены алгебраические дополнения элементов соответствующих столбцов матрицы А , называется взаимной для А.

Таким образом, взаимная матрица Ã получается из матрицы А заменой каждого элемента на его алгебраическое дополнение с последующим транспонированием. Ясно, что понятие взаимной матрицы имеет смысл для любой квадратной матрицы как особенной, так и не особенной.

Теорема . Для взаимной матрицы Ã квадратной матрицы А n-того порядка мы имеем А Ã= Ã А=Е , где  =|E| и Е – единичная матрица n-того порядка.

Литература. Осн...7 [ 54-58], доп. 26 [121-133]

Контрольные вопросы и задачи

1.Запишите выражение для обратной матрицы методом разбиения ее на произведение двух треугольных матриц. Напишите формулы преобразования?

2. Какая матрица называется неособенной матрицей ?

3. Какая матрица называется особенной?

4. Составьте обратную матрицу, используя алгебраические дополнения?

Лекция 7

Тема лекции : Методы решения нелинейных уравнений состояния электрической системы. Метод простой итерации. Метод Зейделя. Условия сходимости решения системы линейных уравнений.

Конспект лекции

1. Итерационные методы расчета. Метод простой итерации

Решение нелинейного уравнения (системы нелинейных уравнений), описывающего (описывающих) состояние электрической цепи, может быть реализовано приближенными численными методами. Решение находится следующим образом: на основе первой, достаточно грубой, оценки определяется начальное значение корня (корней), после чего производится уточнение по выбранному алгоритму до вхождения в область заданной погрешности.

Наиболее широкое применение в электротехнике для численного расчета нелинейных резистивных цепей получили метод простой итерации и метод Ньютона-Рафсона, основные сведения о которых приведены в табл. 1.

Найдем решение системы линейных уравнений

a₁₁x₁+a ₁₂ x₂+ …+ a_1nx_n =b₁

a₂₁x₁+a ₂₂ x₂+ …+ a_2nx_n =b₂ (1)

…………………………..

a_n1x₁+a _n2 x₂+ …+ a_nnx_n =b_n

Пусть с помощью некоторого прямого метода вычислены приближенные значения неизвестных

x⁰₁ , x⁰₂ , x⁰₃ , x⁰_n . Подставляя эти значения в левые части системы (1) получаем некоторые значения b⁰ _i отличные от b_i.

a₁₁x ⁰₁+a ₁₂ x ⁰₂+ …+ a_1xx ⁰_n =b ⁰₁

a₂₁x ⁰₁+a ₂₂ x ⁰₂+ …+ a_2xx ⁰_n =b ⁰₂ (2)

…………………………..

a_n1x ⁰₁+a _n2 x ⁰₂+ …+ a_nnx ⁰_n =b ⁰_n

введем обозначения: ⁰_i = погрешности значений неизвестных,

r⁰_i - вязки, т.е. ⁰_i = x_i –x ⁰_i ; r_i⁰ = b_i-b_i⁰, i=1,2,3,…n (3)

Вычитая каждое уравнение системы (2) из соответствующего уравнения системы (1) с учетом обозначений (3) получаем:

a₁₁ ⁰₁+a ₁₂  ⁰₂+ …+ a_1n ⁰_n =r ⁰₁

a₂₁ ⁰₁+a ₂₂  ⁰₂+ …+ a_2n ⁰_n = r ⁰₂ (4)

…………………………..

a_n1⁰₁+a _n2  ⁰₂+ …+ a_nn ⁰_n = r ⁰_n

Решая эту систему , находим значения погрешностей  ⁰_i , которые используем в качестве поправок к решению. Следующие приближения неизвестных имеют вид

х¹₁ = х⁰₁ +  ⁰₁, х¹₁ = x⁰₂ +  ⁰₂ , ……., x¹_n = x⁰_n +  ⁰_n ;

Таким же способом можно найти новые поправки к решению  ¹_i и следующие приближения переменных x² _i = x¹_i + x¹_n = x⁰_n +  ⁰_n ;и т.д. Процесс продолжается до тех пор, пока все очередные значения погрешностей  _i не станут достаточно малыми. Блок-схема алгоритма метода итераций.

Таблица 1. Итерационные методы расчета

Последователь-ность расчета	Геометрическая иллюстрация алгоритма		Условие сходимости итерации	Примечание
Метод простой итерации 1.Исходное нелинейное уравнение электрической цепи f(X)=0 , где –x искомая переменная, представляется в виде x=h(x). 2. Производится расчет по алгоритму xm+1=h(xm), где m=1,2,3,.. шаг итерации.	Здесь - заданная погрешность		На интервале между приближенным и точным значениями корня должно выполняться неравенство |dh(x)/dx|<1	1.Начальное приближение x0 обычно находится из уравнения f(x)=0 при пренебрежении в нем нелинейными членами. 2. Метод распространим на систему нелинейных уравнений n-го порядка. Например, при решении системы 2-го порядка x1=h(x1, x2); итерационные формулы имеют вид ; x1(m+1)=h1(x1m, x2m); x2(m+1)=h2(x1m, x2m); 3. При решении системы уравнений сходимость обычно проверяется в процессе итерации.
Метод Ньютона- -Рафсона 1. На основании исходного нелинейного уравнения электрической цепи f(x)=0, где x -искомая переменная, записывается итерационная формула xm+1= xm- f(xm)/f (xm), где m=1,2,3… - шаг итерации. 2.По полученной формуле проводится итерационный расчет		Здесь  - заданная погрешность	На интервале между приближенным и точным значениями корня должны выполняться неравенства |df(x)/dx|<>0 d2f(x)/dx2<>0 Примечания п. 1,2 и 3 к методу простой итерации распространимы на метод Ньютона-Рафсона. При этом при решении системы f1(x,y)=0 f2(x,y)=0	2-го порядка итерационные формулы имеют вид где

Рассмотренный процесс уточнений решения представляет фактически итерационный метод решения системы линейных уравнений, причем на каждой итерации решаются системы линейных уравнений вида (4) с одной и той же матрицей (1), при разных правых частях. Решение систем уравнений с помощью рассмотренного метода сводится к следующему алгоритму:

1. вводятся коэффициенты уравнений

2. допустимое значение погрешности

3. начальные приближения значений неизвестных