Топологические матрицы

Задать вычислительной машине топологию цепи рисунком затруднительно, так как не существует эффективных программ распознавания образа. Поэтому топологию цепи вводят в ЭВМ в виде матриц, которые называют топологическими матрицами. Выделяют три таких матрицы:

• узловую матрицу,

• контурную матрицу

• и матрицу сечений.

1. Узловая матрица (матрица соединений) – это таблица коэффициентов уравнений, составленных по первому закону Кирхгофа. Строки этой матрицы соответствуют узлам, а столбцы – ветвям схемы.

Для графа на рис. 3 имеем число узлов m=4 и число ветвей n=6. Тогда запишем матрицу А_Н , принимая, что элемент матрицы a_ij (i –номер строки; j –номер столбца) равен 1, если ветвь j соединена с узлом i и ориентирована от него, -1, если ориентирована к нему, и 0, если ветвь j не соединена с узломi . Сориентировав ветви графа на рис. 3, получим

.Данная матрица А_Н записана для всех четырех узлов и называется неопределенной. Следует указать, что сумма элементов столбцов матрицы А_Н всегда равна нулю, так как каждый столбец содержит один элемент +1 и один элемент -1, остальные нули.

Обычно при расчетах один (любой) заземляют. Тогда приходим к узловой матрице А (редуцированной матрице), которая может быть получена из матрицы А_Н путем вычеркивания любой ее строки. Например, при вычеркивании строки “4” получим

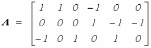
.Число строк матрицы А равно числу независимых уравнений для узлов ,

т.е. числу уравнений, записываемых для электрической схемы по первому закону Кирхгофа. Итак, введя понятие узловой матрицы А, перейдем к первому закону Кирхгофа.

Первый закон Кирхгофа

Обычно первый закон Кирхгофа записывается для узлов схемы, но, строго говоря, он справедлив не только для узлов, но и для любой замкнутой поверхности, т.е. справедливо соотношение

(1)

где  - вектор плотности тока; dS- нормаль к участку dS замкнутой поверхности S.

Первый закон Кирхгофа справедлив и для любого сечения. В частности, для сечения S2 графа на рис. 3, считая, что нумерация и направления токов в ветвях соответствуют нумерации и выбранной ориентации ветвей графа, можно записать

П оскольку в частном случае ветви сечения сходятся в узле, то первый закон Кирхгофа справедлив и для него. Пока будем применять первый закон Кирхгофа для узлов, что математически можно записать, как:

(2)

т.е. алгебраическая сумма токов ветвей, соединенных в узел, равна нулю.

При этом при расчетах уравнения по первому закону Кирхгофа записываются для (m-1) узлов, так как при записи уравнений для всех m узлов одно (любое) из них будет линейно зависимым от других, т.е. не дает дополнительной информации.

Введем матрицу – столбец токов ветвей

= I

Тогда первый закон Кирхгофа в матричной форме записи имеет вид:

АI=0 (3)

– где 0 - нулевая матрица-столбец. Как видим, в качестве узловой взята матрица А, а не АН, т.к. с учетом вышесказанного уравнения по первому закону Кирхгофа записываются для (m-1) узлов.

В качестве примера запишем для схемы на рис. 3

О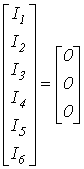 тсюда для первого узла получаем

ч то и должно иметь место.

2. Контурная матрица (матрица контуров) – это таблица коэффициентов уравнений, составленных по второму закону Кирхгофа. Строки контурной матрицы В соответствуют контурам, а столбцы – ветвям схемы.

Элемент b_ij матрицы В равен 1, если ветвь j входит в контур i и ее ориентация совпадает с направлением обхода контура, -1, если не совпадает с направлением обхода контура, и 0, если ветвь j не входит в контур i.

Матрицу В, записанную для главных контуров, называют матрицей главных контуров. При этом за направление обхода контура принимают направление ветви связи этого контура. Выделив в нашем примере (см. рис. 5) дерево, образуемое ветвями 2-1-4, запишем коэффициенты для матрицы В.

Перейдем теперь ко второму закону Кирхгофа.

Под напряжением на некотором участке электрической цепи понимается разность потенциалов между крайними точками этого участка, т.е.

(4)

Просуммируем напряжения на ветвях некоторого контура:

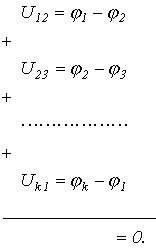
Поскольку при обходе контура потенциал каждой i-ой точки встречается два раза, причем один раз с “+”, а второй – с “-”, то в целом сумма равна нулю.

Таким образом, второй закон Кирхгофа математически записывается, как:

(5)

• и имеет место следующую формулировку: алгебраическая сумма напряжений на зажимах ветвей (элементов) контура равна нулю. При этом при расчете цепей с использованием законов Кирхгофа записывается независимых уравнений по второму закону Кирхгофа,

• т.е. уравнений, записываемых для контуров, каждый из которых отличается от других хотя бы одной ветвью. Значение топологического понятия “дерева”: дерево позволяет образовать независимые контуры и сечения и, следовательно, формировать независимые уравнения по законам Кирхгофа. Таким образом, с учетом (m-1) уравнений, составленных по первому закону Кирхгофа, получаем систему из

уравнений, что равно числу ветвей схемы и, следовательно, токи в них находятся однозначно.

Введем столбцовую матрицу напряжений ветвей

U=

Тогда второй закон Кирхгофа в матричной форме записи имеет вид

BU = 0. (6)

В качестве примера для схемы рис. 5 имеем

откуда, например, для первого контура получаем

ч то и должно иметь место.

Если ввести матрицу-столбец узловых потенциалов

 =

причем потенциал последнего узла  =0 , то матрица напряжений ветвей и узловых потенциалов связаны соотношением

U=A^Т  (7)

где A^Т - транспонированная узловая матрица.

Для определения матрицы В по известной матрице А=А_ДА_С , где А_Д – подматрица, соответствующая ветвям некоторого дерева, А^С- подматрица, соответствующая ветвям связи, может быть использовано соотношение В= (-А^Т_С А^-1Т _Д1).

3. Матрица сечений – это таблица коэффициентов уравнений, составленных по первому закону Кирхгофа для сечений. Ее строки соответствуют сечениям, а столбцы – ветвям графа.

Матрица Q , составленная для главных сечений, называется матрицей главных сечений. Число строк матрицы Q равно числу независимых сечений.

Элемент q_ij матрицы Q равен 1, если ветвь входит в i-е сечение и ориентирована согласно направлению сечения (за положительное направление сечения принимают направление ветви дерева, входящей в него), -1, если ориентирована противоположно направлению сечения, и 0, если ветвь j не входит в i-е сечение.

В качестве примера составим матрицу Q главных сечений для графа на рис. 5. При указанной на рис. 5 ориентации ветвей имеем

В заключение отметим, что для топологических матриц А, В и Q, составленных для одного и того же графа, выполняются соотношения

АВ^Т= 0; (8)

QВ^Т= 0, (9)

которые, в частности, можно использовать для проверки правильности составления этих матриц. Здесь 0 – нулевая матрица порядка 0 .

Приведенные уравнения позволяют сделать важное заключение: зная одну из топологических матриц, по ее структуре можно восстановить остальные.

Понятие о параметрах модели

Параметры модели

Физические величины, которые характеризуют модель независимо от ее текущего динамического состояния. К параметрам относятся: сопротивления¹ (электрическое, магнитное, термальное, гидравлическое, механическое, акустическое, ротационное, и т.д.); отношения сопротивлений (коэффициенты передачи); меры инерционности (постоянные времени).

¹⁾ Если речь идет о сопротивлениях реактивного характера, то в качестве параметров могут выступать физические величины их определяющие (например, индуктивность катушки, емкость конденсатора, и т.д.).

Выбор шага симуляции и метода интегрирования

Шаг симуляции

Фундаментальный параметр процесса симуляции компьютерной модели. Равен интервалу между временными значениями, для которых вычисляются все координаты модели (т.е. рассчитывается весь поток процедур и функций реализующий модель).

При компьютерном моделировании существенными следует считать четыре источника погрешности:

• Трансцендентные функции, которые вычисляются компьютерным путем аппроксимации полиномиальными или степенными рядами:

• Д 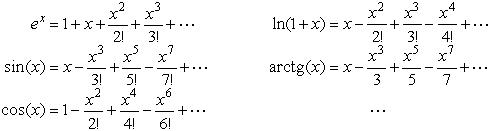искретный квазианалог интегратора (блок 1/S).

• Итерационный решатель (тот или иной классический алгоритм, предназначенный для решения алгебраических уравнений путем подбора независимых переменных до заданной точности).

• Математический сопроцессор компьютера, чья дискретная природа требует округлений, которые, в свою очередь, обычно проявляются в виде шума при дифференцировании меняющихся в большом диапазоне параболических сигналов n-ого порядка.

Литература основ. 11[1-100], доп. 21[1-528]

Контрольные вопросы и задачи

1. Сформулируйте основные топологические понятия для электрических цепей.

2. Что такое узловая матрица?

3. Что такое контурная матрица?

4. Что такое матрица сечений?

5 . Токи ветвей некоторой планарной цепи удовлетворяют следующей полной системе независимых уравнений:

Восстановив граф цепи, составить матрицы главных контуров и сечений, приняв, что ветвям дерева присвоены первые номера.

Ответ:

6. Составить матрицу главных контуров для графа на рис. 3, приняв, что дерево образовано ветвями 2, 1 и 5

Ответ:

B=

7. Решить задачу 5, используя соотношения (8) и (9).

Лекция 5.

Тема лекции : Методы решения линейных уравнений Понятие точных и приближенных методов решений линейных алгебраических уравнений. Применение метода Гаусса в матричной форме, Крамера и т.д Достоинства и недостатки

Конспект лекции

Решение системы линейных алгебраических уравнений методом Гаусса. Пусть дана система m линейных уравнений с n неизвестными Ax=b Требуется найти ее общее решение, если она совместна, или установить ее несовместность. Предлагаемый алгоритм называется методом Гаусса или методом последовательного исключения неизвестных. Выпишем расширенную матрицу системы

Н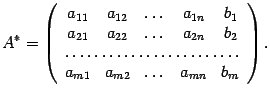 азовем элементарными операциями следующие действия с матрицами:

• перестановка строк;

• умножение строки на число, отличное от нуля;

• сложение строки с другой строкой, умноженной на число.

Отметим, что при решении системы уравнений, в отличие от вычисления определителя и нахождения ранга, нельзя оперировать со столбцами.

Если по матрице, полученной из A* выполнением элементарной операции, восстановить систему уравнений, то новая система будет равносильна исходной.

Цель алгоритма -- с помощью применения последовательности элементарных операций к матрице A* добиться, чтобы каждая строка, кроме, быть может, первой, начиналась с нулей, и число нулей до первого ненулевого элемента в каждой следующей строке было больше, чем в предыдущей.

Шаг алгоритма заключается в следующем. Находим первый ненулевой столбец в матрице A*. Пусть это будет столбец с номером i Находим в нем ненулевой элемент и строку с этим элементом меняем местами с первой строкой. Чтобы не нагромождать дополнительных обозначений, будем считать, что такая смена строк в матрице А* уже произведена, то есть a_1i0. Тогда ко второй строке прибавим первую, умноженную на число , к третьей строке прибавим первую , умноженную на число , и т.д.

В результате получим матрицу

(Первые нулевые столбцы, как правило, отсутствуют.)

Если в матрице A*₁ встретилась строка с номером k, в которой все элементы a⁽¹⁾_kj равны нулю, а b_k⁽¹⁾0 то выполнение алгоритма останавливаем и делаем вывод, что система несовместна

Д ействительно, восстанавливая систему уравнений по расширенной матрице, получим, что k-ое уравнение будет иметь вид

Этому уравнению не удовлетворяет ни один набор чисел x₁,x₂,x₃,…x_k.

М атрицу A*₁ можно записать в виде

где

П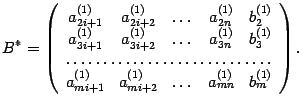 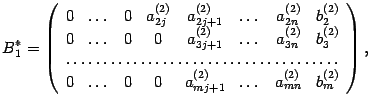о отношению к матрице B* выполняем описанный шаг алгоритма. Получаем матрицу

Где j>i, a_2j⁽²⁾<>0. Эту матрицу можно записать в виде.

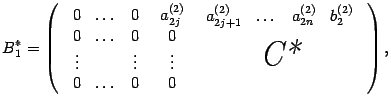
И к матрице С* снова применим описанный выше шаг алгоритма

Процесс останавливается, если после выполнения очередного шага новая уменьшенная матрица состоит из одних нулей или если исчерпаны все строки. Заметим, что заключение о несовместности системы могло остановить процесс и ранее.

Если бы мы не уменьшали матрицу, то в итоге пришли бы к матрице вида

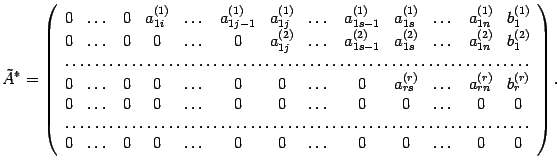
Далее выполняется так называемый обратный ход метода Гаусса. По матрице составляем систему уравнений. В левой части оставляем неизвестные с номерами, соответствующими первым ненулевым элементам в каждой строке, то есть x_i, x_j, x_r. . Заметим, что r=RgA. Остальные неизвестные переносим в правую часть. Считая неизвестные в правой части некоторыми фиксированными величинами, несложно выразить через них неизвестные левой части.

Теперь, придавая неизвестным в правой части произвольные значения и вычисляя значения переменных левой части, мы будем находить различные решения исходной системы Ax=b . Чтобы записать общее решение, нужно неизвестные в правой части обозначить в каком-либо порядке буквами С₁,…,С_n-r. включая и те неизвестные, которые явно не выписаны в правой части из-за нулевых коэффициентов, и тогда столбец неизвестных можно записать в виде столбца, где каждый элемент будет линейной комбинацией произвольных величин С₁,…,С_n-r. (в частности, просто произвольной величиной C_k). Эта запись и будет общим решением системы.

Если система была однородной, то получим общее решение однородной системы. Коэффициенты при C ₁ взятые в каждом элементе столбца общего решения, составят первое решение из фундаментальной системы решений, коэффициенты при C ₂ второе решение и т.д.

Фундаментальную систему решений однородной системы можно получить и другим способом. Для этого одному переменному, перенесенному в правую часть, нужно присвоить значение 1, а остальным – нули. Вычислив значения переменных в левой части, получим одно решение из фундаментальной системы. Присвоив другому переменному в правой части значение 1, а остальным - нули, получим второе решение из фундаментальной системы и т.д.

Решение системы линейных алгебраических уравнений методом Крамера

Процедура решает неоднородную систему n линейных алгебраических уравнений с n неизвестными:

a₁₁ x₁+a₁₂ x₂+ . . .+a_1n x_n=a_1n+1

a₂₁ x₁+a₂₂ x₂+ . . .+a_2n x_n=a_2n+1

. . . .

a_n1 x₁+a_n2 x₂+ . . .+a_nn x_n=a_nn+1

Процедура позволяет найти корни, если определитель основной матрицы A=(a_ij) не равен нулю. Для нахождения i-го корня ищем определитель:

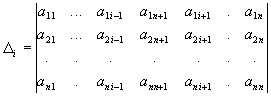
для всех i=1..n. Тогда

В результате получим: если система не имеет решения, то S=0; если система имеет решения S=1, а массив X содержит решения системы. В процедуре вызывается функция вычисления определителя, в качестве которой можно использовать функцию или другую имеющуюся у Вас.

Решение системы линейных алгебраических уравнений методом Халецкого.

Для удобства рассуждений систему запишем в матричном виде:

Ax=b

где A=[a_ij]- квадратная матрица порядка n,

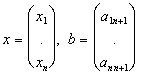
- векторы столбцы. Представим матрицу A в виде произведения нижней треуголной матрицы B=(b_ij) и верхней треугольной матрицы C=(c_ij) с единичной диагональю, т.е.

A=BC

тогда искомый вектор x может быть вычислен из цепи уравнений

By=b, Cx=y

так как матрицы В и C - треугольные, то системы легко решаются.

Процедура не проверяет имеет ли система решение.

Решение системы линейных алгебраических уравнений методом Гаусса.

Процедура решает неоднородную систему n линейных алгебраических уравнений с n неизвестными:

a₁₁ x₁+a₁₂ x₂+ . . .+a_1n x_n=a_1n+1

a₂₁ x₁+a₂₂ x₂+ . . .+a_2n x_n=a_2n+1

. . . .

a_n1 x₁+a_n2 x₂+ . . .+a_nn x_n=a_nn+1

Вначале находим отличный от нуля коэффициент при x₁. Соответствующее уравнение переставляем с первым (если это необходимо). Получаем систему с a₁₁ отличным от нуля. Разделив коэффициенты этого уравнения на a₁₁, получим:

x₁+b₁₂ x₂+ . . .+b_1n x_n=b_1n+1

При помощи этого уравнения исключаем x₁ из исходной системы:

a⁽¹⁾₂₂ x₂+a⁽¹⁾₂₃ x₃+ . . .+a⁽¹⁾_2n x_n=a⁽¹⁾_2n+1

. . . .

a⁽¹⁾_n2 x₂+a⁽¹⁾_n3 x₃+ . . .+a⁽¹⁾_nn x_n=a⁽¹⁾_nn+1

где

a⁽¹⁾_{i j}=a_{i j}-a_{i 1}b_{1 j}, i,j= 2...n

Полученная система содержит n-1 уравнение. Применяем описанную выше процедуру к этой системе. Операции повторяем требуемое число раз, пока не приведем систему к треугольному виду:

x₁+с₁₂ x₂+ . . .+с_1n x_n=с_1n+1

x₂+ . . .+c_2n x_n=c_2n+1

. . . .

x_n=c_nn+1

Теперь легко определить x_n,x_n-1, . . ., x₁.

Если det(A)=0, то исходная система не имеет решений и процедура выдает S=0 иначе S=1 и решения находятся в массиве X.

Решение системы линейных алгебраических уравнений методом Гаусса с частичным выбором главного элемента

Процедура решает неоднородную систему n линейных алгебраических уравнений с n неизвестными:

a₁₁ x₁+a₁₂ x₂+ . . .+a_1n x_n=a_1n+1

a₂₁ x₁+a₂₂ x₂+ . . .+a_2n x_n=a_2n+1

. . . .

a_n1 x₁+a_n2 x₂+ . . .+a_nn x_n=a_nn+1

В отличии на каждом шаге мы ищем не просто отличный от нуля коэффициент при x_k, а максимальный из них по абсолютной величине, в остальном практически также схема приведения системы к треугольному виду:

с₁₁x₁+с₁₂ x₂+ . . .+с_1n x_n=с_1n+1

с₂₂x₂+ . . .+c_2n x_n=c_2n+1

. . . .

с_nnx_n=c_nn+1

Если det(A)=0, то исходная система не имеет решений и процедура выдает S=0 иначе S=1 и решения находятся в массиве X. Выбор на каждом шаге максимального по абсолютной величине коэффициента, позволяет получить малые невязки при решении системы.

Решение системы линейных алгебраических уравнений методом вращений.

Вновь решаем систему n линейных уравнений Ax=b. Вначале приведем матрицу A к нижне-треугольному виду преобразованиями вращения:

A=L*R_{n-1 n} ... R_{1 2}

здесь L - нижняя треугольная матрица (т.е. элемент l_{i j}=0, если j > i), а R_{i j} - матрица вращения. Матрица вращения это "почти единичная" матрица у которой r_{i i}=r_{j j}=cos(u), и r_{i j}=-r_{j i}=sin(u). Действительно нетрудно проверить, что умножая, например, матрицу 2-го порядка

| cos(u) sin(u)|

R= | |

|-sin(u) cos(u)|

на некоторый вектор x, мы осуществим поворот этого вектора на угол u относительно начала координат. Заметим, что определитель матрицы врщения равен 1, и R_{i j}*R^T_{i j}=E, т.е. обратная матрица совпадает с транспонированной.

Итак представив исходную матрицу в виде произведения нижней треугольной матрицы на последовательность матриц вращения, мы можем решить вначале систему Ly=b, а затем систему R_{n-1 n} ... R_{1 2}x=y. Первая система легко решается благодаря простому виду матрицы L, а вторую систему нетрудно разрешить, благодаря свойствам матрицы вращения.

Несколько слов непосредственно о реализации алгоритма. Вначале последовательно для каждого ненулевого элемента расположенного выше главной диагонали матрицы A находится преобразование вращения, которое переводит его в нуль. Для хранения преобразование вращения R_{i j} достаточно хранить соответствующий угол u, но проще хранить t=tg(2u), тогда

cos(u)=(1-t²)/(1+t²)

sin(u)=2t/(1+t²)

В результате последовательности преобразований, в массиве A будет, непосредственно матрица L(a[i,j]=l_{i j}, i≥j; l_{i j}=0, i< j) и соответствующие преобразование R_{i j} (a[i,j]=t_{i j}, i<j, здесь t_{i j} - тангес удвоенного угла вращения для преобразования R_{i j}). Теперь решаем вначале систему Ly=b, а затем из вектора y, получаем решения исходной системы обращая преобразования вращения.

Решение системы линейных алгебраических уравнений методом отражений.

Вновь решаем систему n линейных уравнений Ax=b. Вначале приведем матрицу A к верхнетреугольному виду преобразованиями отражений:

Q_n-1 ... Q₂*Q₁*A*S = R,

здесь Q_i - соответствующие матрицы отражения, S -результирующая матрица перестановок, R - верхняя треугольная матрица.

Теперь решив треугольную систему

R*Y=Q_n-1 ... Q₂*Q₁*b

нетрудно определить решение исходной системы

X=S*Y

Чуть подробнее о реализации алгоритма. Вначале находим преобразования отражения, применяя их к матрице A и вектору b. Затем решаем полученную систему, помещая решение в вектор X, и, наконец, переставляем элементы вектора X используя вектор S, который содержит информацию о перестановках в исходной матрице A.

Литература. Осн...7 [ 41-47 ], доп. 26 [121-133]

Контрольные вопросы и задачи

1. В чем заключаются преимущества использования матричных методов расчета?

2. В чем заключается сущность метода Гаусса?

3. Запишите формулу расчета по методу Гаусса ?

4. Что означает прямой и обратный ход Гаусса?

Лекция. 6

Тема лекции : Применение метода обратной матрицы при решении систем линейных уравнений. Представление обратной матрицы в виде простейших сомножителей. Критерий сходимости.

Конспект лекции