Литература. Основ. 2 стр.[7-15] Доп.22 [1-100 ] Контрольные вопросы

1. Что такое электрическая система и из каких элементов она состоит?

2. Режимы и процессы. Различные виды режимов и процессов в электриче­ских системах.

3. Что понимается под статической и динамической устойчивостью системы?

4. Предмет изучения и цели курса «Переходные процессы».

5. Нелинейность и ее виды в электрической системе.

Лекция 2

Тема лекции: Понятие математической модели. Численные методы решения алгебраических и трансцендентных уравнений. Метод бисекций.

Конспект лекции

Понятие математической модели. Проблематика, задачи и цели моделирования

В теории моделирования основными являются проблемы: разработки универсальных подходов к построению моделей, точности симуляции движения их координат, оценки величин погрешностей, адекватности получаемых результатов, идентификации изучаемых систем, синтеза технических устройств и гипотез.

Задачи общей теории моделирования заключаются в решении перечисленных проблем. При поиске решений используются:

1. Методы теории подобия

2. Методы теории расчета цепей

3. Методы теории систем автоматического управления

4. Численные методы

Глобальными целями моделирования являются вопросы изучения природы систем, возможностей их структурного развития и прогнозирование поведения

Явный решатель моделирующей программы

Это библиотека классических подпрограмм (функций), которые реализуют операцию интегрирования. (Дискретные квазианалоги интеграторов используются для решения дифференциальных уравнений).

Неявный (итерационный) решатель моделирующей программы

Это библиотека классических подпрограмм, которые предназначены для решения алгебраических уравнений путем итерационного подбора независимых переменных.

Оптимизирующий решатель моделирующей программы

Э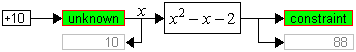 то разновидность неявного решателя, которая предназначена для минимизации значения функции в процессе итерационного подбора ее независимых переменных.

Рис.1

На рис.1 показана техника подключения неявного решателя (блоков unknown и constraint – неизвестная и нулевой_баланс) к алгебраическому полиному с целью поиска корней уравнения.

На каждом шаге симуляции неявный решатель, в итерационном процессе, подбирает такое значение на выходе блока неизвестная (этот блок, по сути, является генератором сигнала), которое, будучи подставлено в полином обнулит его. За фактом обнуления следит датчик решателя – блок нулевой_баланс. Если инициировать решатель (блок неизвестная) разными начальными значениями, то можно найти оба корня.

Понятие о структурном и мультидоменном физическом моделировании

Структурное моделирование

Техника моделирования основанная на использовании моделей в виде преобразующих сигналы блоков. Связи между входными и выходными сигналами устанавливаются посредством задания передаточных функций. Поскольку структурные блоки имеют выраженные входы и выходы, построенные согласно этой технике модели иногда называют направленными сигнальными графами (см. рис. 1).

Мультидоменное физическое моделирование

Техника моделирования основанная на использовании универсальной библиотеки моделей элементов физических устройств, из которых можно составлять схемы физические принципиальные. Поскольку в энергетических цепях поток материи может менять направление, построенные согласно этой технике модели иногда называют ненаправленными или бинаправленными сигнальными графами (см. рис. 2).

Естественно-физическое моделирование

Переходная техника физического моделирования не использующая модели элементов физических устройств и предполагающая задание системы уравнений либо в графической, либо в текстовой форме (см. рис. 3).

Математический аппарат теории систем автоматического регулирования предполагает исключение алгебраических уравнений со свободными переменными из моделей технических устройств. Таким образом, техника структурного моделирования, использующая модели в форме передаточных функций, требует наличия лишь явного решателя. Явный решатель подключается ко всем интеграторам модели (блоки 1/S), и, с той или иной точностью (на что влияет выбор метода интегрирования), интегрирует соответствующие сигналы, обеспечивая тем самым решение дифференциальных уравнений.

Численные методы решения нелинейных алгебраических уравнений и систем, составляющие основу итерационного решателя моделирующих программ

Решить систему уравнений [f(xⁿ)] = 0 численно — значит найти, а точнее подобрать (подогнать) такие значения [xⁿ], которые обнулят систему полиномов [f(xⁿ)]. В процессе подгонки, по текущим результатам нужно принимать решение о том, какие значения искомых переменных [xⁿ⁺¹] подставлять в следующий раз (n – индекс текущего приближения корня). Для этого существуют разные методы.

Приближенное решение уравнения методом деления пополам (метод бисекций)

Пусть задана непрерывная функция f(х) и требуется найти корень уравнения f(х)=0. Предположим, что найден отрезок [а,b] такой, что . Тогда согласно теореме Больцано-Коши внутри отрезка [а,b] существует точка c, в которой значение функции равно 0, то есть f(с)=0, c (а, b). Итерационный метод бисекций состоит в построении последовательности вложенных отрезков {[а_n,b_n]|[а_n,b_n] [а_n-1,b_n-1] [a,b]}, на концах которых функция принимает значения разных знаков. Каждый последующий отрезок получают делением пополам предыдущего. Процесс построения последовательности позволяет найти нуль функции f(х) (корень уравнения f(х)=0) с любой заданной точностью.

Опишем один шаг итераций. Пусть на (n-1)-м шаге найден отрезок [а_n-1,b_n-1] [a,b], такой, что f(а_n-1)f(b_n-1)< 0. Делим его пополам точкой =(а_n-1+b_n-1)/2 и вычисляем f(). Если f()=0, то =(а_n-1+b_n-1)/2 - корень уравнения. Если f() 0, то из двух половин отрезка выберем ту, на концах которой функция имеет противоположные знаки, так как один из корней лежит на этой половине. Таким образом,

a_n=a_n-1, b_n= , если f( )f(а_n-1)<0,

a_n= , b_n=b_n-1, если f( )f(а_n-1)>0.

Если требуется найти корень с точностью , то деление пополам продолжаем до тех пор, пока длина отрезка не станет меньше 2 . Тогда координата середины отрезка и есть значение корня с требуемой точностью .

Метод бисекций - простой и надежный метод поиска простого корня уравнения f(х)=0. Он сходится для любых непрерывных функций f(х), в том числе не дифференцируемых. Скорость сходимости невелика. Для достижения точности необходимо совершить N итераций, где

.

Это означает, что для получения каждых трех верных десятичных значений необходимо совершить около 10 итераций.

Е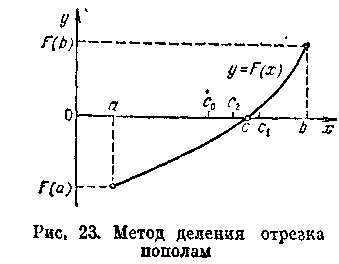 сли на отрезке [а,b] находятся несколько корней уравнения f(х)=0, то процесс сходится к одному из них. Метод неприменим для отыскания кратных корней четного порядка. В случае кратных корней нечетного порядка он менее точен. Это один из простейших методов нахождения корней нелинейных уравнений. Рассмотрим графическую иллюстрацию метода. Пусть для определенности F(a)< 0, F(b)>0 (pиc.1). В качестве начального приближения корня примем с₀ = (a + b)/2. Поскольку в

рассматриваемом случае f(с₀)<0, то cо < с < b, и рассматриваем только отрезок [с₀, b]. Следующее приближение: c₁ =(с₀ + b)/2. При этом отрезок [с₁, b] отбрасываем, поскольку F(c₁)> 0 и F(b)> 0, т. е. с₀ < с < с₁. Аналогично находим другие прибли­жения: с₂ = (с₀ + c₁)/2 и т. д.

Выполнить приближенное вычисление с точностью  корня уравнения (5.1) методом половинного деления при условии, что f(x) непрерывна [а;b] и f(а)*f(b)<0, можно, например, по следующей алгоритму:

Шаг 0. Задать концы отрезка а и b, функцию f, малое число  >0 (допустимую абсолютную погрешность корня или полудлину его промежутка неопределенности), малое число >0 (допуск, связанный с реальной точностью вычисления значения данной функции); вычислить (или ввести) f(a).

Шаг 1. Вычислить с = 0.5 (а + b).

Шаг 2 Вычислить F(a)

Шаг 3. Если b - а<2, положить =с (- корень) и остановиться.

Шаг 4. Вычислитьf(с).

Шаг 5. Если |f(с)| < , положить =с и остановиться.

Шаг 6. Еслиf(а)f(с) < 0, положить b= с и вернуться к шагу 1; иначе положить а= с, f(а)=f(с) и вернуться к шагу 1.

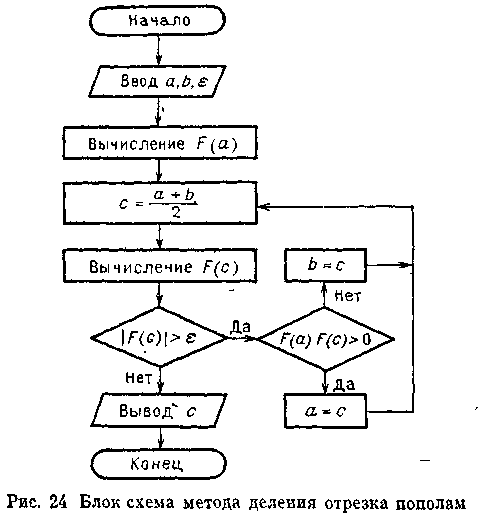
Рис.2 Блок-схема метода деления отрезка пополам.

Литература Осн.7[16-39]. Доп. 26[155-161]

Контрольные вопросы

1.В сущность метода дихотомии?

2. Условие останова метода?

3. Какова сходимость метода?

4. Назовите формулу подсчета количества итераций?

5. Методом деления отрезка пополам найти с погрешностью 10-³ хотя бы один корень уравнений: а) 2е^х = 5х; б) х²cos2х = = -1.

6. Составить блок-схему решения уравнения методом хорд.

7. Найти с погрешностью 10~³ методом хорд хотя бы один ко­рень уравнений: а) 2х - Lgx - 7 = 0; б) ctgx — 0.1=0.

Лекция 3

Тема лекции : Приближенное решение уравнений методом простых итераций и Ньютона, хорд.

Конспект

Метод простых итераций (метод последовательных приближений) решения уравнения f(x)=0 состоит в замене исходного уравнения эквивалентным ему уравнением х= (х) и построении последовательности x_n-1= (х), сходящейся при n к точному решению. Сформулируем достаточные условия сходимости метода простых итераций.

Теорема. Пусть функция (х) определена и дифференцируема на [а,b], причем все ее значения (х) [а,b]. Тогда, если существует число q, такое, что | '(х)| q < 1 на отрезке [а,b], то последовательность x_n+1 = (x_n) (n=0,1,2, ... ,) сходится к единственному на [а,b] решению уравнения х = (x) при любом начальном значении x₀ [а,b], т. е.

= = , f( )=0, [a,b].

При этом, если на отрезке [a,b] производная '(х) положительна, то

,

если '(х) отрицательна, то

.

Опишем один шаг итераций. Исходя из найденного на предыдущем шаге значения x_n-1, вычисляем у = (х_n-1). Если |у - х_n-1|> , полагают х_n=у и выполняют очередную итерацию. Если же |у - х_n-1|< , то вычисления заканчивают и за приближенное значение корня принимают величину х_n=у. Погрешность полученного результата зависит от знака производной (х). При '(х)>0 корень найден c погрешностью q /(1-q), если '(х)<0, то погрешность не превышает .

П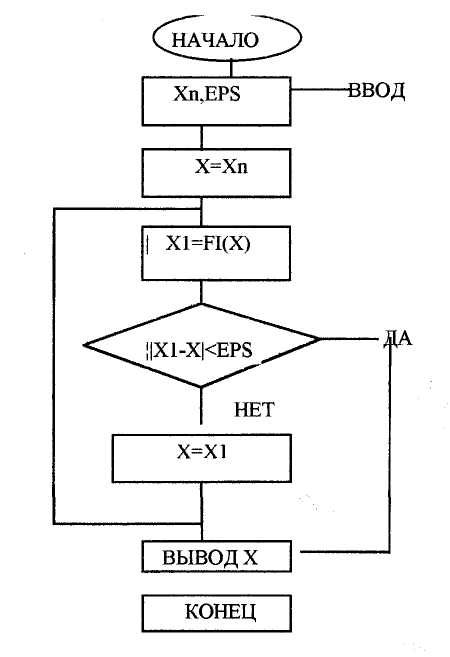 ри использовании метода простых итераций основным моментом является выбор функции (х) в уравнении х= (х), эквивалентному исходному. Для метода итераций следует подбирать функцию (х) так, чтобы | '(х)| q<1. При этом следует помнить, что скорость сходимости последовательности {x_n} к корню тем выше, чем меньше число q.

Пусть известно начальное приближение х=с₀. Подставляя это значение в правую часть уравнения x=f(x) получаем новое приближение с₁= f(с₀). Итерационный процесс прекращается если результаты двух последовательных итераций близки | с_т+1 – с_т|< и достаточным условием сходимости явялется условие |f’(c_n)|<1.

На рисунке 2 представлена блок-схема метода простой итерации

Рис.2 -Блок-схема метода простой итерации

Необходимо установить, при каких условиях итерационный процесс будет сходиться к корню уравнения (рис.3)

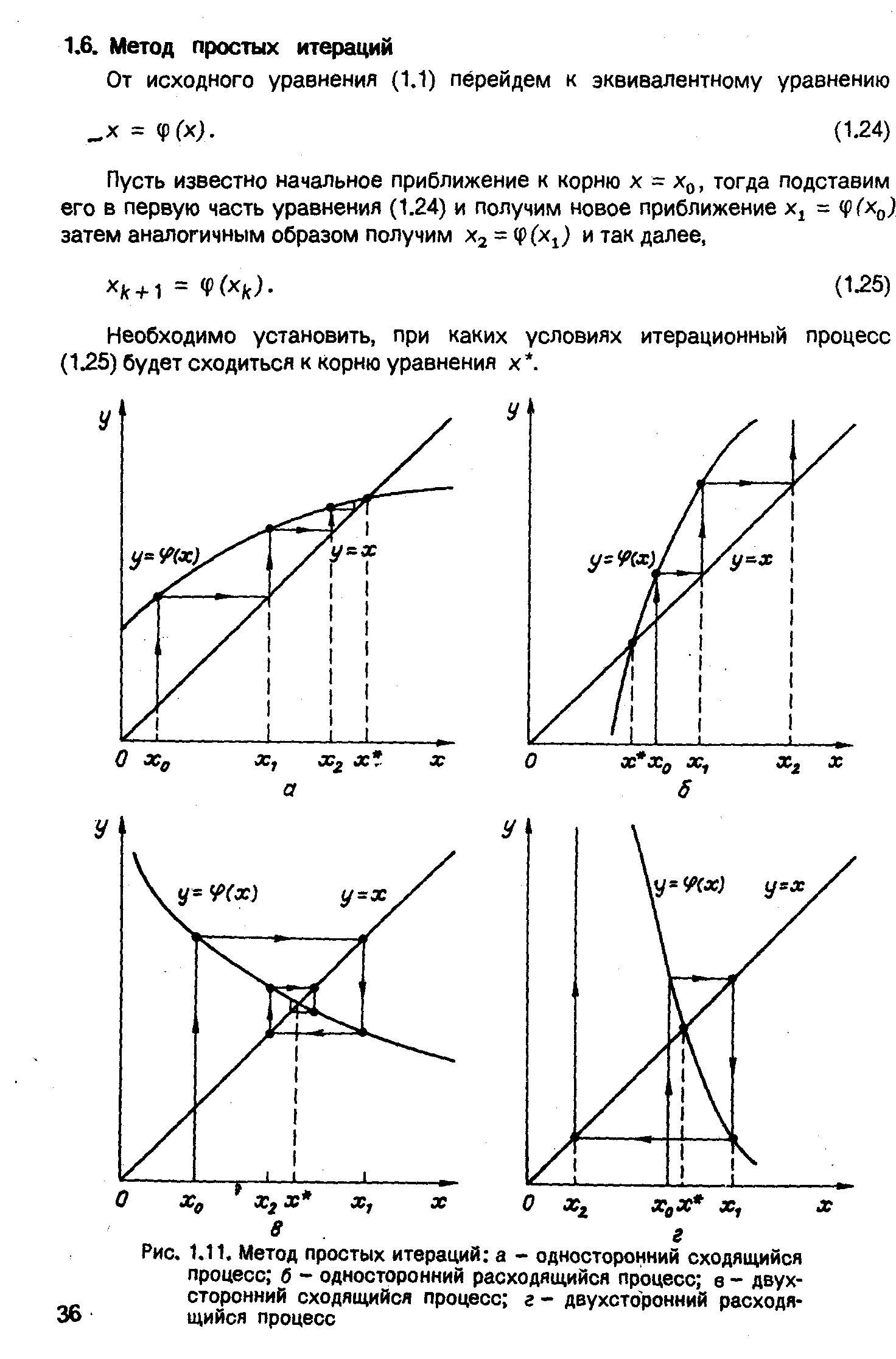
Рис.3- Метод простых итераций : а- односторонний сходящийся процесс; б- односторонний расходящийся процесс; в- двухсторонний сходящийся процесс; г- двухсторонний расходящийся процесс;

Приближенное решение уравнения f(x)=0 методом Ньютона

Если известно хорошее начальное приближение решения уравнения f(х)=0, то эффективным методом повышения точности является метод Ньютона (метод касательных). Метод состоит в построении итерационной последовательности x_n-1=x_n-f(x_n)/ (x_n), сходящейся к корню уравнения f(x)=0. Сформулируем достаточные условия сходимости метода.

Теорема. Пусть f(х) определена и дважды дифференцируема на [a,b], причем f(а)f(b)<0, а производные (х), (х) сохраняют знак на отрезке[a,b]. Тогда, исходя из начального приближения x₀ [a,b], удовлетворяющего неравенству f(x₀) (x₀)>0, можно построить последовательность

x_n+1 = x_n f(x_n) / (x_n), n = 0,1,2, ...,

сходящуюся к единственному на [а,b] решению уравнения f(х)=0.

Метод Ньютона допускает простую геометрическую интерпретацию. Если через точку с координатами (x_n,f(x_n)) провести касательную, то абсцисса точки пересечения этой касательной с осью Ох и есть очередное приближение x_n+1 корня уравнения f(х)=0. f’(x)=tg().

Для оценки погрешности n-го приближения корня можно воспользоваться неравенством

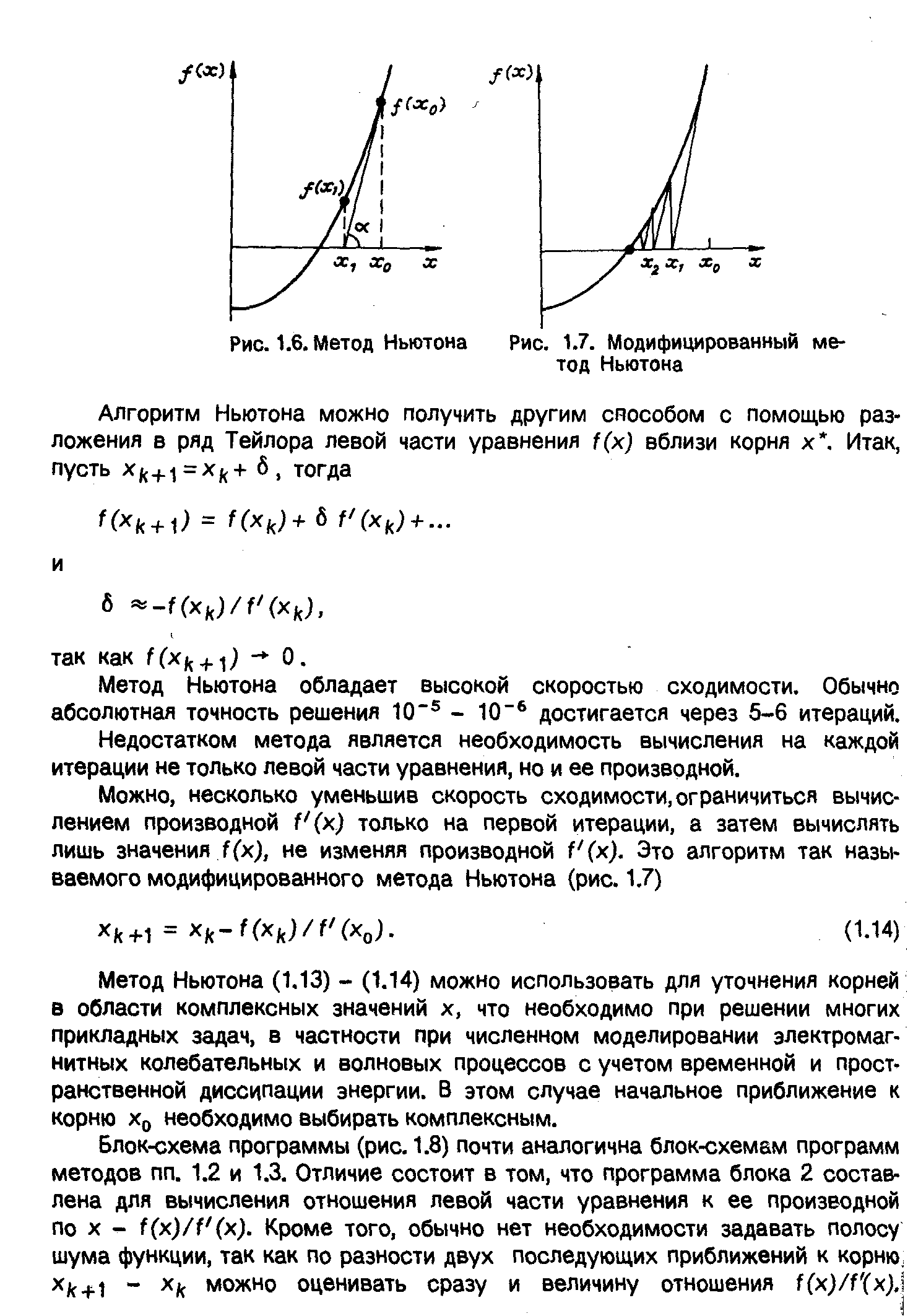
Рис.4 а – Метод Ньютона; б- Модифицированный метод Ньютона

,

где М₂ - наибольшее значение модуля второй производной | (х)| на отрезке [а,b]; m₁ - наименьшее значение модуля первой производной | (x)| на отрезке [а,b]. Таким образом, если | x_n - x_n-1 | < , то

| - x_n | M₂ ² /(2m₁). Последнее соотношение означает, что при хорошем начальном приближении корня после каждой итерации число верных десятичных знаков в очередном приближении удваива­ется, то есть процесс сходится очень быстро. Значит, если необходимо найти корень с точностью , то итерационный процесс можно прекращать, когда

| x_n - x_n-1 | < ₀ = .

Опишем один шаг итераций. Если на (n - 1)-м шаге очередное приближение x_n-1 не удовлетворяет условию окончания процесса, то вычисляем величины f(x _n-1), (x _n-1) и следующее приближение корня х_n=x_n-1-f(x_n-1)/ ( x_n-1). При выполнении условия

| x_n - x_n-1 | < .

Величину x_n принимаем за приближенное значение корня , вычисленное с точностью . Блок-схема этого алгоритма изображена на рисунке А3.

Метод Ньютона эффективен, если известно хорошее начальное приближение для корня и в окрестности корня график функции имеет большую крутизну. В том случае процесс быстро сходится. Если же численное значение производной (х) вблизи корня мало, то процесс вычисления корня может оказаться очень долгим.

Формула метода Ньютона

xⁿ⁺¹ = xⁿ - f(xⁿ) / f '(xⁿ) ,

[xⁿ⁺¹] = [xⁿ] - [f '(xⁿ)]^-1 [f(xⁿ)] .

Метод Ньютона-Рафсона предполагает возможность относительного изменения шага итерации a:

[xⁿ⁺¹] = [xⁿ] - [f '(xⁿ)]^-1 [f(xⁿ)] aⁿ .

Модифицированный метод Ньютона предполагает замораживание инверсной матрицы производных (инверсного Якобиана) на первом шаге:

[xⁿ⁺¹] = [xⁿ] - [f '(x⁰)]^-1 [f(xⁿ)] .

Но в этом случае наблюдается лишь линейное схождение. Хотя, через несколько итераций, инверсный Якобиан можно обновлять.

Метод секущих:

xⁿ⁺¹ = xⁿ - f(xⁿ) (xⁿ - x^n-1) / (f(xⁿ) - f(x^n-1)) .

Здесь невозможно вести речь об оценке производной конечной разностью, поскольку шаг итерации очень большой. В VisSim'е, переменной xⁿ соответствует блок "неизвестная", а блок "нулевой баланс" считывает с модели значение функции f(xⁿ). Приведенные же выше формулы используются для расчета значения на выходе блока "неизвестная" на следующем шаге итерации.

Основные итерационные методы сходятся весьма быстро. Для того чтобы текущее приближение стало более чем в миллион раз ближе к корню, методу дихотомии требуется 40 итераций, методу золотого сечения – 29, методу Ньютона еще меньше. Очевидно, что линейные системы уравнений решаются за одну итерацию.

Метод хорд. Пусть требуется вычислить действительный корень урав­нения f(х) = 0, изолированный на отрезке [а, b] Рассмотрим график функции у=f(х). Пусть f(a)<0 и f(b) > 0. Точки графика A [a; f (а)] и В[b; f (b)] соединим хордой За приближенное значение искомого корня примем абсциссу х₁ точки пересечения хорды АВ с осью 0x

Это приближенное значение находится по формуле

где x₁ принадлежит интервалу ]а, b[. Пусть, например, f (x₁) < 0, тогда за новый (более узкий) промежуток изоляции корня можно принять [х₁, b]. Сое­динив точки a_i[x_i; f (x₁)] и B[b; f (b)], получим в точке пересечения хорды с осью Ох второе приближение х₂, которое вычислим по формуле

и т. д. Последовательность чисел а, х₁, x₂, ... стремится к искомому корню уравнения f(x) = 0. Вычисление приближенных значений корней уравнения следует вести до тех пор, пока не перестанут изменяться те десятичные знаки, которые мы хотим сохранить в ответе (т. е. пока не будет достигнута задан­ная степень точности).

Если х—точный корень уравнения f(x) = 0, изолированный на отрезке [a, b], а —приближенное значение корня, найденное методом хорд, то оцен­ка погрешности этого приближенного значения такова.

Литература. Основ. 7 стр.[21-29] Доп.26 [ 155-161]

Контрольные вопросы

1. Дайте определение теоремы Больцано-Коши?

2. Условие окончания итерационного процесса при использовании метода простой итерации?

3. Оценка погрешности метода хорд?

3. Формула определения приближенного значения корня по методу простой итерации?

4. Формула определения приближенного значения корня по методу Ньютона?

5. Формула определения приближенного значения корня по методу хорд?

6. В чем сущность модифицированного метода Ньютона?