Блок-схема эвристического алгоритма реализации задачи линейного программирования

В том случае, когда отсутствует стандартное программное обеспечение, нет необходимости сводить обобщенную постановку задачи к канонической. В этом случае необходимо разработать эвристический анализ или соответствующую программу.

В основе эвристических алгоритмов для реализации методов математического программирования лежит следующая блок-схема:

1. Определяются области возможного изменения (диапазоны) неизвестных переменных x₁, x₂, x₃,....., x_n.

2. Организуется, с определенным шагом, перебор возможных вариантов значений x₁, x₂, x₃,....., x_n.

3. При каждом сочетании значений параметров x₁, x₂, x₃,....., x_n, проверяются все условия и ограничения и если они соответствуют заданным, рассчитываются значения целевой функции.

4. При этом запоминается то значение целевой функции, которое является экстремальным.

5. После того, как все возможные сочетания x₁, x₂, x₃, ... , x_n рассмотрены, оптимальным является тот план, при котором значение целевой функции достигает экстремального значения.

При составлении эвристического алгоритма для нашего примера 2, диапазоны изменения величин следующие:

0x₁12, 0x₂6, 0x₃2, 0x₄43, 0x₅32

При постановке задач следует обращать внимание также на условие целочисленности.

Вопросами целочисленных решений занимается раздел математики, называемый дискретным программированием.

Литература Осн. 24[1-50] , 23[1-20]

Контрольные вопросы:

1. Математическая запись ОЗЛП?

2. Какой план называется допустимым, оптимальным?

3. Из какого набора неизвестных составляется единичный базис.

Лекция 11.

Тема лекции : Закрытая и открытая модели транспортной задачи.

Особенности транспортной задачи

Симплексный метод является универсальным методом решения любых задач линейного программирования. Однако отдельные типы задач линейного программирования (например, о назначении и транспортные) в силу специфичности своей структуры могут решаться более простыми методами. К транспортным задачам относится большое число задач планирования перевозок грузов. Кроме того, ряд других задач (например, задача размещения промышленности) могут быть сведены к транспортной.

Напомним классическую формулировку и модель транспортной задачи.

Имеется n поставщиков однородного груза, i-й поставщик имеет запас груза a_i(i=1,2,…,n) и m потребителей, j-й потребитель имеет потребность в грузе b_j(j=1,2,…,m). Затраты на перевозку груза от i–го поставщика j-му потребителю составляют c_ij. Требуется определить объемы грузоперевозок от i–го поставщика к j–му потребителю x_ij, при которых достигается минимальная суммарная стоимость перевозок

n m

  c_ijx_ij

i=1 j=1

При этом запас груза должен быть вывезен, т.е.

xi1+xi2+…+xij+…+xin=ai (i=1,2,…,n), (111)

а потребности всех потребителей удовлетворены, т.е.

x1j+x2j+…+xij+…+xmj=bi (j=1,2,…,m). (112)

Рассматривается закрытая модель, при которой

m n

 b_j=  a_i,

j=1 i=1

т.е. суммарные запасы груза равны потребности в нем. Любая задача может быть сведена к закрытой путем введения фиктивного поставщика (если b_j  a_i) или фиктивного потребителя (если  b_j   a_i).

Транспортная задача имеет следующие особенности:

• все ограничения задачи имеют вид равенств;

• каждая переменная входит всего в два ограничения;

• коэффициенты при переменных в ограничениях равны единице.

Благодаря этим особенностям, транспортная задача может быть решена более простым способом, чем симплексный. Причем симплексная матрица для транспортной задачи состоит из нулей и единиц.

Для решения транспортной задачи составляют специальную матрицу (табл.35).

Транспортная матрица совмещает матрицу стоимостей c_ij и объемов перевозок x_ij . В этой матрице по срокам записаны ограничения по запасам сырья у поставщиков (111), а по столбцам – по потребности потребителей (112).

В отличие от задач линейного программирования транспортная задача всегда имеет оптимальное решение. Для доказательства этого утверждения покажем, сто система ограничений совместна (т.е. имеется опорное решение) и что целевая функция ограничена.

Обозначим суммарный объем перевозок через М

m n

M =  b_j=  a_i,

j=1 i=1

Таблица 35

Постав щик	Потребитель						Запасы
	B1	B2	...	Bj	...	Bm
A1	C11 X11	C12 X12	...	C1j X1j	...	C1m X1m	a1
A2	C21 X21	C22 X22	...	C2j X2j	...	C2m X2m	a2
...	...	...	...	...	...	...	...
Ai	Ci1 Xi1	Ci2 Xi2	...	Cij Xij	...	Cim Xim	ai
...	...	...	...	...	...	...	...
An	Cn1 Xn1	Cn2 Xn2	...	Cnj Xnj	...	Cnm Xnm	an
Потреб ность	b1	b2	...	bj	...	bm

Предположим, что

X_ij = a_ib_j/M

Подставляя это значение xij в ограничения (111) и (112)

m m m

 x_ij=  a_ib_j/M =a_i/M  b_j=a_i

j=1 j=1 j=1

m m m

 x_ij=  a_ib_j/M =b_j/M  b_j=b_j

j=1 j=1 j=1

получаем, что все ограничения выполняются и, следовательно, ... дает опорное решение задачи.

Для доказательства ограниченности целевой функции выбираем максимальную и минимальную стоимость перевозок и обозначаем соответственно max c_ij = C₁ и min c_ij = C₂.

Тогда значение целевой функции

n m n m

W=   c_ijx_ij  C₁   x_ij,

i=1 j=1 i=1 j=1

n m n m

W=   c_ijx_ij  C₂   x_ij.

i=1 j=1 i=1 j=1

Так как n m

  x_ij=M

i=1 j=1

то C₁MWC₂M, т.е. общее решение задачи ограничено сверху и снизу.

Общее количество базисных переменных в транспортной задаче равно (m + n – 1), так как среди (m+n) ограничений-равенств задачи является линейно-зависимым (поскольку суммарные потребности и запасы равны, то, складывая равенства систем (111) и (112), можно получить одно и то же уравнение).

Решение транспортной задачи линейного программирования включает два основных этапа: построение опорного решения (начального плана перевозок) и построение оптимального решения.

Разберем последовательно методы получения опорного и оптимального решений.

Построение опорного решения

Опорное решение транспортной задачи может быть получено следующими методами: северо-западного угла; наименьших стоимостей и двойного предпочтения.

Наиболее простым и легко формализуемым является метод северо-западного угла, однако он дает обычно решение, далекое от оптимального. При построении опорного решения методами наименьших стоимостей и двойного предпочтения анализируется матрица затрат и начальный план обычно близок к оптимальному.

Метод северо-западного угла используется, как правило, при расчетах на ЭВМ. При его применении данные о стоимостях не нужны. Ниже приведено построение опорного решения этим методом. Рассматривается клетка 11 (северо-западный угол) и в нее на основании сравнения величин a1 и b1 проставляется максимальный объем перевозок (минимальная из величин a1 и b1). Если b1<a1, то первый столбец из рассмотрения исключается, так как потребности первого потребителя удовлетворены (x11 = b1) и определяется разность a1 – b1 (остаток запасов у первого поставщика). Далее рассматривается клетка 12 (новый северо-западный угол) и сравниваются величины b2 и (a1 – b1). В клетку 12 проставляется минимальная из этих величин. Если (a1 –b1) b2, то далее рассматривается клетка 22 (новый северо-западный угол) и сравниваются величины a2 и b2-(a1-b1) (оставшаяся потребность у второго потребителя). Подобная процедура повторяется вплоть до заполнения всей матрицы.

Пример 7. Пусть условия транспортной задачи заданы матрицей (табл.36). Перед построением опорного решения проверим баланс запасов и потребления, т.е. является ли модель закрытой.

Суммарные запасы (_i=1³a_i) составляют 40+80+240=360 единиц груза, а суммарная потребность (_i=1⁴b_j)– 20+200+60+120=400 единиц груза.

Так как суммарная потребность превышает объем запасов, вводим четвертого фиктивного поставщика, таким образом, чтобы модель стала закрытой, т.е.

4 3

a₄=  b_j-  a_i=400-360=40.

j=1 i=1

В результате получим новую матрицу для закрытой модели (табл.37), причем стоимости перевозок от фиктивного поставщика равны 0.

Приступим теперь к построению опорного решения.

1. Проставляем в клетку 11 минимальный из объемов a1 и b1 min a,b = 40,20 = 20 (табл./38).

2. Находим разность a1 – b1 = 40 –20 = 20.

Таблица 36

Постав щик	Потребитель				Запасы
	В1	В2	В3	В4
А1	3	5	4	6	40
А2	5	3	7	8	80
А3	4	6	3	5	240
Потреб ность	20	200	60	120

Таблица 37

Постав щик	Потребитель				Запасы
	В1	В2	В3	В4
А1	3	5	4	6	40
А2	5	3	7	8	80
А3	4	6	3	5	240
А4	0	0	0	0	40
Потреб ность	20	200	60	120

Таблица 38

Постав щик	Потребитель				Запасы
	В1	В2	В3	В4
А1	20 3	20 5	4	6	40
А2	5	80 3	7	8	80
А3	4	100 6	60 3	80 5	240
А4	0	0	0	40 0	40
Потреб ность	20	200	60	120

3.Рассматриваем новый северо-западный угол – клетку 12 и сопоставляем b2 и (a1 – b1). Определяем min{b2, a1 – b1} = 20 и записываем его в клетку 12.

4.Находим разность b2 – (a1 – b1) = 200 – 20 = 180. минимальную из этих величин (а2) проставляем в клетку 22.

5.Находим разность [b2–(a1-b1)–a2] = 200-20-80=100.

6.Рассматриваем клетку 32 и так далее до заполнения всей матрицы.

Опорное решение показано в табл. 38.

Суммарная стоимость перевозки при этом решении составляет

n m

W=   c_ijx_ij=20*3+20*5+80*3+ 100*6+60*3+80*5+40*0=1580

i=1 j=1

При применении метода наименьших стоимостей последовательно заполняют клетки, содержащие наименьшие стоимостные показатели. При этом в эти клетки записывают максимально допустимый объем перевозок, для чего сопоставляют объемы запасов и потребности. Процедура повторяется до получения допустимого решения.

При построении опорного решения транспортной задачи методом двойного предпочтения поочередно просматриваются все строки и столбцы матрицы. Клетки, содержащие минимальные удельные затраты на перевозку в каждой строке и столбце, помечаются каким-то знаком (например, V). Первоначально объемы перевозок проставляются в клетках, отмеченных дважды, т.е. предпочтительных как в строке, так и в столбце (отсюда и название метода). После того, как клетки, помеченные дважды, заполнены полностью, объемы проставляются в клетки, отмеченные один раз. И затем с учетом ограничений по ai и bj заполняются остальные клетки.

Таблица 40

Постав щик	Потребитель				Запасы
	В1	В2	В3	В4
А1	20 3	20 5	4	6	40
А2	5	80 3	7	8	80
А3	4	60 6	60 3	120 5	240
А4	0	40 0	0	0	40
Потреб ность	20	200	60	120

Пример 9. Составить опорное решение для рассматриваемой ранее транспортной задачи (см. табл. 37) методом двойного предпочтения.

Просматриваем строки и отмечаем клетки, имеющие минимальные стоимости (табл.40). Это клетки 11, 22 и 33. Затем просматриваем столбцы и также отмечаем клетки с минимальными стоимостями (11, 22, 33 и 34). Таким образом, клетки 11, 22 и 33 отмечены дважды – проставляем в них возможные объемы перевозок (соответственно 20, 80 и 60). Далее рассматриваем клетку 34 и ставим в нее объем перевозки.

Больше помеченных клеток нет, и дальнейшее заполнение матрицы можно производить, опираясь на метод наименьших стоимостей. Опорное решение приведено в табл.40. Как видно из составления табл.40, в рассматриваемом примере опорные решения, полученные методом наименьших стоимостей и двойного предпочтения, совпадают.

Получение оптимального решения транспортной задачи методом потенциалов

Одним из наиболее простых и распространенных методов оптимизации транспортной задачи является метод потенциалов. Условия оптимальности плана транспортной задачи вытекают из теорем двойственности и заключаются в следующем.

Для того чтобы допустимый план транспортной задачи Х=xijm,n был оптимальным, необходимо и достаточно, чтобы ему соответствовала система чисел U1,U2,…,Un,V1,V2,…,Vm, именуемых потенциалами, удовлетворяющая условиям

Vj-Uicij, если xij=0; (113)

Vj-Ui=cij, если xij0 (114)

(i=1,2,…,n; j=1,2,…,m).

Условия (113) и (114) называются условиями потенциальности оптимального плана транспортной задачи и формулируются следующим образом: для того чтобы решение транспортной задачи было оптимально, необходимо и достаточно, чтобы оно было потенциально.

Условия потенциальности показывают, что разность потенциалов потребителя и поставщика равна стоимости перевозки между ними, если перевозка осуществляется – условие (113) и меньше стоимости перевозки при ее отсутствии – условие (114).

Алгоритм решения транспортной задачи методом потенциалов состоит из двух этапов: предварительного и общего.

I Первый этап включает:

1. построение опорного решения;

2. присвоение и расчет системы потенциалов;

3. проверка первоначального плана на оптимальность.

Если опорное решение не является оптимальным, то переходят ко II второму этапу, который включает:

1. улучшение плана перевозок;

2. исправление системы потенциалов;

3. проверка улучшенного плана на оптимальность.

Общий шаг циклически выполняется до получения оптимального плана перевозок.

Рассмотрим подробнее составные части метода потенциалов.

Построение опорного решения (I-1) осуществляется методами северо-западного угла, наименьших стоимостей или двойного предпочтения.

Расчет системы потенциалов (I-2) производится на основании второго условия оптимальности (114).

Всего необходимо присвоить (n+m)потенциалов, а допустимый невырожденный план включает (n+m-1) перевозку.

Используя занятые клетки для расчета потенциалов, можно составит систему из (n+m-1) уравнений с (n+m) переменными. Такая система имеет неограниченное множество решений. Поэтому для построения системы потенциалов надо задаться потенциалом одного поставщика или потребителя (строки или столбца). Обычно полагают U1=0, либо присваивают нулевой потенциал строке, имеющей занятую перевозкой клетку с наибольшей стоимостью. Далее потенциалы всех остальных столбцов и строк вычисляют через занятые клетки, используя второе условие оптимальности (114).

Проверка плана на оптимальность (шаги I-3 и II-3) проводится для клеток, не занятых перевозками. Очевидно, что для клеток с перевозками второе условие оптимальности выполняется, так как оно было использовано для присвоения системы потенциалов. Для всех незанятых клеток проверяется выполнение первого условия оптимальности (113). Для этого вычисляют невязку ij=Vj-Ui-cij. Если ij0 для всех клеток, то план является оптимальным, так как первое условие оптимальности соблюдено. Если имеются положительные превышения, то первое условие оптимальности не соблюдено и план может быть улучшен. Величина ij показывает, какая экономия на перевозку единицы груза может быть достигнута при изменении плана перевозок.

Рис.11. Примеры циклов

Улучшение плана перевозок заключается в выборе (II-1) с максимальным превышением и составлении замкнутого контура (цикла), вершинами которого являются клетка в нарушением и клетка с перевозками. Контур может иметь различную конфигурацию (рис.11), но в нем всегда четное число вершин. Начиная с клетки, имеющей нарушение, вершины контура нумеруются (по часовой стрелки или против). Нечетные вершины составляют положительную полуцепь, а четные – отрицательную. При улучшении плана в вершинах положительной полуцепи объемы перевозок увеличатся, а в вершинах отрицательной полуцепи уменьшатся. Далее просматривают объемы перевозок в четных клетках и находят минимальный из них q=minxij. После этого перераспределяют объемы перевозок внутри контура, для чего к объемам перевозок в нечетных вершинах прибавляют объем q, а из объемов перевозок в четных вершинах вычитают эту величину. В результате этой процедуры получают улучшенный план, в котором общие затраты на перевозку меньше, чем в предыдущем плане на величину qij. Новый план является допустимым, так как в каждой строке и столбце замкнутого контура в одной клетке объем увеличился, а в другой уменьшился на одну и ту же величину.

Проверке улучшенного плана на оптимальность(II-3) предшествует исправление системы потенциалов (шаг II-2). Для этого необязательно строить новую систему потенциалов, можно исправить прежнюю.

Предположим, что второе условие оптимальности нарушено для клетки, в которой ранее не было перевозки, т.е. клетки с максимальным нарушением (первой вершины контура). Следовательно, необходимо исправит потенциал Vj для этой клетки на величину нарушения ij. Если в данном столбце нет больше клеток (занятых), то можно переходить к проверке первого условия оптимальности. Если же в столбце есть клетки с перевозками, то, исправив потенциал столбца на ij, нарушим условия оптимальности на ij для остальных занятых клеток столбца. Чтобы исправить потенциалы этих клеток, достаточно соответствующую им величину Ui уменьшить на ij, т.е. новые потенциалы строк составят U’i=Ui-ij. Затем просматриваем строки, где потенциалы изменились. Если в этих строках имеются занятые клетки (кроме клеток столбца Vj, у которого уже изменился потенциал), то потенциалы столбцов, соответствующих этим клеткам, исправляются на величину ij. Далее аналогично просматриваем новые столбцы и т.д. Процесс перерасчета потенциалов заканчивается, когда при просмотре строк или столбцов в них не окажется клеток с поставками.

Литература Осн. 25[1-50], доп 23[1-50].

1. Дайте классическую формулировку транспортной задачи (ТЗ)?

2. Математическая запись ТЗ?

3. Математическая запись открытой и закрытой модели ТЗ?

4. Опишите методику решения ТЗ методом потенциалов?

Лекция 12.

Тема лекции : Численные методы решения нелинейных дифференциальных уравнений. Метод Эйлера с прогнозом и коррекцией. Их достоинства и недостатки .

Приближенное решение задачи Коши методом Эйлера.

Д.у. n-порядка в качестве неизвестных величин входит функция y(x) и ее первые n-производные по аргументу x.

 (x, y, y^’, ,y(n))=0 (1)

ей эквивалентно

_к(x_, y, y₁, y₂, ,y_n, y_n’)=0. (2)

Уравнения 1 и 2 имеют множество решений, поэтому нужные единственные решения выделяют с помощью дополнительных условий.

В зависимости от таких условий рассмотрим 3 типа задач, для которых доказано единственность решения.

Первый тип - это задачи Коши - для таких задач, кроме уравнения (1) должны быть заданы некоторые точки x_o – начальные значения, т.е. значения функции y(x) и ее производных.

y(x_o)=y_{o ,} y^`(x_o)=y₁₀, ……, y^n-1(x_o)= y_1n-1,₀.

Ко второму типу относятся так называемые граничные или краевые задачи, для которых дополнительные условия задаются в виде функциональных отношений между искомыми решениями. Причем порядок ОДУ=2

Третий тип задачи для ОДУ – это задачи на собственные значения. В этих задачах задаются функция y(x), ее n-производных, дополнительно включается m-неизвестных ₁…_n – которые называются собственными значения. В качестве примера к ним относятся задачи определения частот, структуры электромагнитных полей, задачи нахождения фазовых коэффициентов.

К численному решению ОДУ мы обращаемся, когда не удается построить аналитическое решение задачи через известные функции.

1. Метод Эйлера.

Систему 1 можно представить в каноническом виде, т.е. в форме Коши

(3)

Уравнение 3 дополняется начальными условиями:

y₁(x₀)=y₁₀; y₂(x₀)=y₂₀,…,y_n(x₀)=y_n0 (4)

Для простоты рассмотрим уравнение (3 ) задачи Коши для уравнения (1), а затем обобщим для системы из n уравнения:

(5)

Разложим в ряд Тейлора уравнение (5) в окрестности точки x₀:

(6)

При малых значений n-ограничимся 2 числами уравнения ( 6):

В точке x_o+h при малых значений h ограничимся 2 членами уравнения (6)

y(x_o+h) =y_o+hy΄(x_o)+Q(h²) (7)

Q(h²) – бесконечно малая величина порядка h².

Заменим производную y΄(x_o) в формуле (7) на правую часть уравнения (5)

y(x₁+h)=y_o+hf(x_,y) (8)

Теперь приближенное решение точки x₁=x_o+h можно снова рассматривать как начальное условие для решения и по формуле ( 8) и найти снова новое значение функции в точке x₂=x₁+h

В результате получим простейший алгоритм для решения задачи Коши, который называется методом Эйлера или методом ломаных – это означает, что мы заменили функцию y(x) отрезком касательных к этой функции в узле x_0,x , x₂

Формулу (8) можно получить из уравнения (5) следующим образом, заменим производную в левой части уравнения (5) приближенным конечно-разностным уравнением.

(9)

На каждом шаге метода Эйлера решение у(х) определяется с погрешностью Q(h), т.к. мы отбросили члены ряда Тейлора пропорциональных h в степени выше первой.

М етод Эйлера имеет локальную погрешность 2-го порядка. Глобальная погрешность имеет 1-порядок, и при постоянном шаге h=const применима первая формула Рунге :

(10)

y_h(x) - приблизительное значение уравнения в полученной точке x с шагом h; y_kh(x) - приблизительное значение того же уравнения в полученной с шагом kh; P – порядок метода.

Эта формула позволяет опытным путем определить шаг h.

Программа описывающая метод Эйлера. Описание программы.

Program Eiler;

Type vec=array [1..8]of real;

Var P,x,x9,h:real; y: vec;

Procedure RP (x: real; var y, f:vec);

Begin F[1]=y[2]

F[2]= (Sqr (P/x)-1)*(y[1]-y[2]/x);

end;

Procedure ЕUL (N: integer; x, h: real; var y: vec);

Var I: integer; F: vec,

begin

RP(x,y,f);

For i: =1 to n Dо

y [i]=y[i]+h*F[i];

end;

Begin

Repeat write (‘введите P, x, x9, H, y[1],y[2]’);

Readln (P, x, x9, H, y[1],y[2]’);

While (x<x9)and (h>0) Dо

Begin

EUL (2,x,h,y);

Writeln (x:8:2, y[1],y[2], y[i]);

end;

Until false;

end.

Метод Эйлера в программе описан в виде процедуры EUL имеющий параметры: n– число уравнений в системе, x – начальная точка, h – шаг интегр., y – массив размерности n для начальных условий результатов. RP – имя подпрограммы для вычисления правых частей системы ОДУ. Последний формальный параметр F:vec позволят из одной программы обращаться к решению разных систем ОДУ. Обе подпрограммы имеют общий параметр P. В качестве примера для решения выбрано уравнение y”+y’(x*1(1-p²)x²)y=0

Чтобы решить уравнение перейдем от диф. уравнения второго порядка y”+y’(x*1(1-p²)x²)y=0 к системе двух уравнений первого порядка :

y^’(x)=y₂(x),

y’₂(x)=(p²/x²-1) y₁(x)-y₂(x)/x

в форме Коши.

Обозначим неизвестную функцию y (x) через y₁ (x) а ее производную y^’(x), через y₂(x) получим ОДУ.

Литература Осн.7 [177-182], 26 [205-227]

Контрольные вопросы

1. Напишите вывод формулы Эйлера?

2. Какова погрешность метода Эйлера?

3. Покажите геометрическую интерпретацию метода Эйлера?

Лекция 13.

Тема: Численные методы решения нелинейных дифференциальных уравнений. Методы Рунге-Кутта и их достоинства и недостатки Методы Рунге-Кутта с переменным шагом интегрирования. Методы Адамса и Милна

Конспект лекции

Методы Рунге – Кутта 2-ого порядка.

Для уменьшения погрешности интегралов в обычных дифференциальных уравнениях (ОДУ) используются разложения искомого выражения в ряд Тейлора. Необходимо учитывать большое количество членов этого ряда. Однако это влечет за собой необходимость аппроксимации производной от правой частей ОДУ. Идея метода Рунге – Кутта заключается в том, что производные аппроксимируются через значение уравнения y=f(x,y), в точках на интервале [x_o, x_o+h] из условия наибольшей близости алгоритма нахождения к ряду Тейлора в зависимости от старшей степени h . Рассчитывается схема Рунге – Кутта разных порядков точности. Запишем для 2-ого порядка однопараметрическое уравнение:

y(x_o+h)=y_o+h[(1- )f_o+ f(x₀+yh, y₀+yf₀h)]+Q(h³) (11)

Здесь равна обычно параметр или .

Локальная погрешность уравнения (11) имеет третий порядок, глобальная имеет 2 порядок. В 1 случае, когда локальная погрешность уравнения (11) принимает следующий вид:

y(x₀+h)=y₀+h[f₀+f(x₀+h,y₀+hf₀)]/2 (12)

Геометрическая интерпретация функции представлена на рис.1,2 следующим образом:

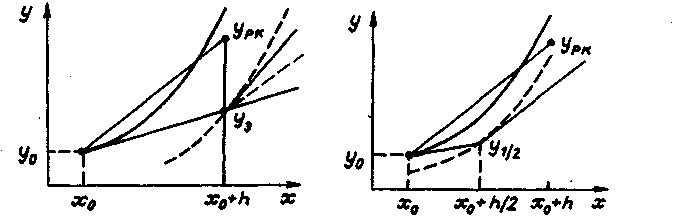
Рис. 1. Метод Рунге- Кутты второго Рис. 2. Метод Рунге-Кутты второго порядка (. = 1)

порядка (= 0,5)

Описание геометрической интерпретации метода Рунге – Кутта с разной точностью

1. Вначале вычисляется приближенное значение ОДУ в точках x₀+h по формуле Эйлера y_э=y₀+h,f₀.

2. Затем определяется наклон интегральной кривой в найденной точке f(x₀+h,y_э).

3. После нахождения среднего наклона на шаге h, находим уточненное значение y_эк=y(x₀+h).

4. Схема такого поиска решения называется прогноз-коррекция, что означает грубое вычисление по формуле нижнего порядка (Эйлера). Затем уточняем с учетом полученной информации по формуле высшего порядка (Рунге - Кутта).

5. Для погрешности алгоритма 2: для решения системы ОДУ запишем с учетом того, что y₀=y_э- hf₀.

Запишем в новом виде: y_k(x₀+h)=y_кэ+h[f_ko-f_k(x₀+h,y_кэ)]/2

6. Рассчитаем формулу для в следующем виде:

y=(x₀+h)=y₀+hf(x₀+ ,y₀+hf/2).

Алгоритм при .

1. Вычисляем методом Эйлера функцию в точке y_1/2=y₀+x₀ +h/2.

2. Находим касательную наклонную к интегральной кривой в этой точке, затем уточняем ее по методу Рунге – Кутта.

Запишем программу для решения задачи Коши предназначенной для вычисления ОДУ с помощью: 1) 2) , вариантов метода Рунге – Кутта 2-ого порядка.

В программе схемы Рунге – Кутта 2-ого порядка реализованы в виде подпрограммы Рунге – Кутта 21 и Рунге – Кутта 22. РК – 22 с формальными параметрами что и в подпрограмме методом Эйлера.

1. Program RK211;

Type vec=array[1..8] of real;

var p,x,x9,h:real, var y, F:real);

Procedure RP ( x:real; var y,f:vec);

Begin

f[1]:=y2; f[2]:=(sqr(p/x)-1.0)*y[1]-y[2]/x);

end;

Procedure RK21 (N:integer; var x,h:real; var y:vec);

var I:integer; H2:real; F₀,F:vec;

begin

H₂:=H/2; RP(x,y,f₀);

for i:=1 to n do

y[i]:=y[i]+H*F₀[i];

x:=x+h; RP(x,y,f);

for i:=1 to n do

y[i]:= y[i]+H₂*(F[i]-F₀[i]);

end;

Begin

Repeat

Write (‘введите P,x,xg,h,y[1],y[2]’);

Readln(x<xg)=(h>0.0) do

Begin

RK21(2,x,h,y);

Writeln (x:10:2, ‘ ‘ ,y[1]:10:2, ‘ ‘ , y[2]:10:2);

end;

Until false;

end.

2. Program RK22;

Type vec=array [1..8] of real;

Var P,x,xg,h:real; y:vec;

Procedure RP (x:real; var y,F:vec);

Begin

F[1]:=y[2]:=(sqr(p/x)-1.0)*y[1]-y[2]/x);

end;

Procedure RK22 (w:integer; var x.h:real; var y:vec);

var i:integer; h2:real; y1,f:vec;

Begin

H2:=H/2; RP(x,y,f);

for i:=1 to n do

y1[i]:=y[i]+h2*f[i]; RP(x+H2; y1,F);

for i:=1 to n do

y1[i]:=y[i]+H*F[i]

end;

begin

Repeat write (‘P,x,xg,h,y[1],y[2]?’);

Readln (P,x,xg,h,y[1],y[2]);

While (x<xg)=(H>0.0) do

begin

RK22 (2,x,h,y);

x:=x+f;

Writeln (x, ‘ ‘ , y[1], ‘ ‘ , y[2]);

end;

Until false;

end.

3) Program RK44;

Type Vec=Array [1..8] Of Real;

Var P,X,X9,H:Real; Y:Vec;

Procedure Rp(X:Real; Var Y,F:Vec>» <* Производные *>

Begin F[1]:=Y[2]; F[2] :=P* (1,0-Sqr(Y[1]) ) *Y[2]-Y[1 ] End;

Procedure Rk4(N:Interer; X,H:Real; Var Y:Vec);

War I,J:Integer; <* Мeтод Рунге-Кутты 4 Порядка *)

H1.H2,Q:Real; Y0» Yl ,Y1,F:Vec; Begin Hl:=0; H2:=H/2;

For I:=L To N Do Begin Y0[I]:=Y[I] У1[I]:=У[I] End;

For J:=L To 4 Do Begin Rp(X+H1,Y,F);

If J=3 Then Hl:=H Else Hl:=H2;

For I: = L To N Do Begin Q:=Hl*F[I]; Y[I]: =Y0[I]+Q;

If J=2 Then Q:=2*Q; Y1[I]:=Yl[I]*Q/3.0;

End

End;

For I:=1 To N Do Y[I]:=Y1[I];

End;

Begin <* Основная Программа Х)

Repeat Write('P,X,X6,H,Y[1],Y[2]?';

Readln(P,X,X9,H,Y[1],Y[2]);

While (Х<Х9) = (Н>0.0) Do Begin Rk4( 2,X,H,Y) ;

X:=X+H; Writeln(X,Y[1],Y[2]) End;

Until False

End.

Метод Адамса

При решении задачи Коши методами Рунге-Кутты необходимо вычислять правые части ОДУ в нескольких точках на каждом шаге. Количество точек зависит от порядка используемого метода. После того как искомая инте­гральная кривая у(х) определена в нескольких точках х₁, х₁,..., х_п, можно применить алгоритмы интерполяции и сократить количество вычислений правых частей ОДУ для получения решения в очередной точке х_{n + 1}. Подоб­ные методы называют многоточечными, или многошаговыми. Известно несколько типов таких методов [5, 7].

Алгоритмы многоточечных методов основываются на аппроксимации интерполяционными полиномами либо правых частей ОДУ, либо интегральных кривых y_k(х).

Рассмотрим четырехточечный вариант одного из методов первого типа для задачи Коши, сформулированной в виде (6.5). С помощью любой из схем, рассмотренных в предыдущих разделах настоящей главы, вычислим решения y1, y2,у3 заданного дифференциального уравнения в точках x₁ x₂, х3. левая часть уравнения f(x, у) на интегральной кривой, соответствующей начальному условию, будет функцией только одного аргумента х

f(x) = f(x,y(x)),

значения, которой в рассматриваемых точках обозначим f₀, f_1, f₂, f₃. В ок­рестности узлов х₀,..., х₃ функцию f(x) приближенно заменим интерпо­ляционным полиномом Ньютона

f (х) ~= f₀ + f₀₁ (x - х_о) + f₀₁₂ (х - х₀) (x-x₁)+ f₀₁₂₃ (х - х₀) (х-х₁)(х- х₂), (1)

где f₀₁, f₀₁₂,f₀₁₂₃ - разделенные разности

Представим искомое решение в точке х₄ = х₃ + h в виде тейлоровского разложения около точки х₃

y₄=y₃ + hf₃+h²/2* f ΄(х₃) + h³/6* f" (х₃) + h³/6* f"' (х₃) + Q (h⁵), (2)

где f΄, f", f" - производные по х от правой части дифференциального уравнения в точке х₃.

Дифференцируя полином (1), получим выражения для производных

f' (Х) = f₀₁ ⁺ f₀₁₂ (х - х₀ + х – x₁ )+ f₀₁₂₃ [(х-х₀)(х-х₁) + + (х-х₀)(х-х₂) + (х- x₁)(x-х₂)],

f" (х) = 2 f₀₁₂ + 2 f₀₁₂₃ (x-x₀+x-x₁+x-x₂), f'"(x) = 6f₀₁₂₃.

Последние соотношения при х = х₃ в случае равноотстоящих узлов после подстановки в них разделенных разностей принимают вид

f (х_э) = (-2 f₀ + 9 f, - 18 f₂ + 11 f₃)/(6 h),

f'(x₃) = (-f₀ + 4 f, - 5 f₂ + 2 f₃)/ h ², (3)

f"' (x₃)= (-f₀ + 3f₁-3f₂ + f_3/)/h³.

Подставляя производные (3) в разложение (2), получим экстраполяционную формулу Адамса

У₄ = X₃ + (55f₃ - 59f_{2 +} 37f₁-9f₀)h/24 + Q(h⁵), (4)

имеющую пятый порядок локальной погрешности и четвертый - глобальной. Изменяя количество членов, учитываемых в ряде (2), можно получить схемы Адамса различных порядков. Остаточный член формулы (4) равен (251/750) h^sf^N(x) [1]. Значительная величина коэффициента в остаточном члене обусловлена тем, что точка х₄ лежит вне интервала расположения узлов [х₀, х₃], по значениям функции f(x),s которых построен интерполяционный полином. То есть мы имеем дело с экстраполяцией, погрешность которой в соответствии с оценкой всегда больше, чем при интерполяции.

С целью уменьшения погрешности способом, аналогичным получению формулы (4), по узлам х₁, х₂, х₃, х₄ строится интерполяционная формула Адамса

У₄ = У₃ + (9f₄ + 19f₃-5f₂ + f₁ )+ Q(h⁵) (5)

Последняя формула является неявной, так как искомая величина у₄ необ­ходима для вычисления значения функции f₄ = f(x₄, y₄), входящего в правую часть. Выражение (5) можно рассматривать как нелинейное уравнение относительно неизвестной величины у₄ . Наиболее часто здесь используется метод простых итераций, хотя в некоторых случаях оказывается более предпочтительным метод Ньютона . Следует иметь в виду, что каждая итерация потребует нового вычисления правой части дифференциального уравнения f(x, у). Решение, определенное по экстраполяционной формуле (4), обычно выбирается в качестве начального приближения для итерационных методов. Поэтому выражение (4) рассматривается как формула прогноза, тогда выражение (5) является формулой коррекции.

Таким образом, вычисления на каждом шаге интегрирования дифферен­циального уравнения осуществляются по схеме Р(ЕС)^mЕ, где этапы вычис­лительного процесса обозначены буквами Р - прогноз; Е - вычисление функции f(x, у); С - коррекция; т - количество итераций коррекции [19]. В[1] приводится эмпирическое правило, согласно которому погрешность решения убывает только до тех пор, пока т << р, где р - порядок исполь­зуемого неявного метода. Следовательно, для метода четвертого порядка не следует выполнять более четырех итераций коррекции. С другой стороны, отмечается, что схема P(EC)^m-1 является более устойчивой в смысле накопления вычислительной погрешности по сравнению со схемой Р(ЕС)^mЕ, следовательно, наиболее выгодной будет схема РЕСЕ. При реали­зации последней схемы на каждом шаге интегрирования осуществляется только одна коррекция.

Формулы (4) и (5) без изменений переносятся на системы ОДУ первого порядка, записанные в форме Коши.

В программе метод Адамса четвертого порядка реализован в виде отдельной подпрограммы с именем AD со следующими формальными параметрами: N - количество уравнений в системе ОДУ; X, Х9, Н - начальное, конечное значения и шаг изменения аргумента х; Y - массив из N начальных значений для каждой из искомых функций y_k (x); RK - имя подпрограммы для получения стартовых значений функций y_k (х) в узлах x_l; х₂, х₃; RP - имя подпрограммы вычисления правых частей ОДУ. В приведенном примере используются фактические имена подпрограмм RK4 и RP, которые оформлены в виде отдельного блока

Type Vec=Array [1..8] Of Real;

Var P, X, X9, H:Real; Y:Vec;

Procedure Rp(X:Real; Var Y,F:Vec); <* Производные *>

Begin F[1]:=Y[2]; F[2]: = (Sqr(P/X)-1.0)*Y[1]-Y[2]/X ;End;

Procedure Rk4(N:Integer; X,H:Real; Var Y:Vec);

Var I,J:Integer; (* Метод Рунге-Kутта 4 Порядка *>

H1,H2, Q:Real; Y0,Y1, f:Vec;

Begin H1:=0.0; H2:=H/2;

For I:=1 To N D0 Begin Y0[i]:=Y[i]; Y1[i]:=Y[i] End;

For J:=1 To 4 Do Begin Rp(X+H1,Y,F);

If J=3 Then H1:=H Else H1:=H2;

For I:=1 To N Do Begin Q:=H1*F[i]; Y[i]:=Y0[i]+Q;

If J=2 Then Q:=2*Q; Y1[i] :=Y1[i]+Q/3.0 End;

End;

For i:=1 To N Do Y[i]:=Y1[i] End;

Procedure Ad(N:Integer, X, X9, H:Real; Var Y:Vec);

Var I, K:Integer; H4:Real; Y1,F,F1:Vec» (*Метод Адамса *)

D:Array [1..2,1..8] Of Real;

Begin H4:=H/24.0; Rp(X,y,f1);

For K:=1 To 3 Do Begin Rk4(N,X,H,y); X:=X+H;

Writeln(X,' ',y[1], ' ', y[2]);

If К<>3 Then Begin Rp(X,Y,F);

For i:=1 To N Do D[k,i]:=F[i]; End;

End;

Repeat Rp(X,y,F);

For I:=1 To N Do

Y1[i]:=Y[i] + H4 * (55.*F[i]–59.*d[2,i] + 37.*d[1,i]–9 *f1[i];

X:=X+H; Rp(x,yl, f1);

For i:=1 To N Do Begin

Y[i]:=Y[i] + h4*(9.*F1[i] + 19* f[i] –5 *d[2,i] + d[1,i]) ;

F1[i]:=D[1,i]; D[1,i]:=D[2,i]; D[2,i]:=F[i];

End;

Writeln(X,' ',Y[1], y[2]);

Until (Х>=Х9)=(Н>0.0);

End;

Begin <* Основная Программа *>

Repeat Write('P,X,X9,H, y[1], Y[2]?');

Readln(P, x, X9, H, y[1], y[2]) ; Ad(2, x, X9, H, y)

Until False

End.

Литература Осн. 7 [182-200] 26 [213-227]

Контрольные вопросы

1. В чем отличие метода Рунге от метода Эйлера?

2. Каким полиномом происходит аппроксимация кривой в методе Адамса?

3. Каковы погрешности вычислений метода Эйлера, Адамса, Рунге?

Лекция 14.

Тема лекции Классификация задач по математическому описанию. Структурные схемы системы и ее элементов. Преобразование структурной схемы.

Конспект лекции

Классификация задач по математическому описанию.

Математическая модель САР

Под математическим описанием или моделью (ММ) понимаются дифференциальные или алгебраические уравнения, выражающие физические, ме­ханические и т.д. представления и закономерности об объекте.

Так как CAP состоит из объекта и автоматического регулятора, то необходимо иметь ММ как объекта, так и регулятора, из которых получают ММ CAP. При создании CAP обычно решают одну из двух задач: - анализа или синтеза.

1. Анализ - имеется система, известны ее параметры, требуется определить свойства системы (устойчивость, качество регулирования).

2. Синтез - задаются свойства системы - необходимо создать систему, удовлетворяющую этим заранее заданным требованиям. Эта задача неоднозначна и сложнее анализа.

В общем виде порядок исследования системы регулирования включает математическое описание системы (формализация данных об объекте регулирования, исследование установившихся и переходных режимов и получение ММ).

В общем случае ММ САР можно записать в виде линейного неоднородного дифференциальнонго уравнения с постоянными коэффициентами:

(2.2)

При исследовании и расчетах систем автоматики широко используется математический метод - преобразование Лапласа. Основанием для этого служит то обстоятельство, что такое преобразование облегчает исследование сложных систем, заменял дифференциальные уравнения алгебраическими.