Среднее и действующее значение синусоидальных тока и эдс
Для количественной оценки синусоидальных функций времени вводятся понятия действующего и среднего значений.
Принято среднее значение функции времени определять за период или полупериод.
.
Для синусоидальной функции среднее значение за период равно нулю.
Среднее значение синусоидальной функции за полпериода:
.
Аналогично,
среднее значение ЭДС за полпериода
.
Действующим значением синусоидальной функции называется её среднеквадратичное значение за период
.
Аналогично для напряжения и ЭДС
,
.
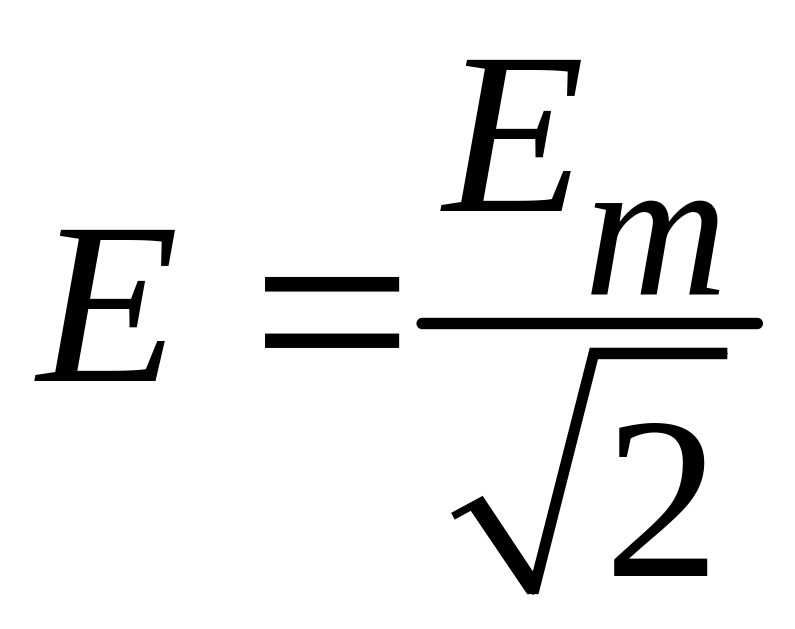Подавляющее большинство приборов, измеряющих синусоидальные токи и напряжения, показывают действующее значение измеряемой величины.
4.2 Особенности физических процессов в цепях переменного тока, реальные и идеальные элементы. Законы Ома, фазовые соотношения, векторные диаграммы, мгновенная и средняя мощности для простейших цепей синусоидального тока (цепи с резистором, индуктивностью и конденсатором.
Синусоидальные ЭДС, напряжения и токи можно изображать графически в виде соответствующих синусоид, такие графики в электротехнике называют волновыми диаграммами (рис. 1).
Обычно на одной волновой диаграмме изображают несколько синусоид переменных величин (напряжений, токов), относящихся к одной и той же цепи. Для оценки их взаимного расположения вдоль оси абсцисс вводится разность их начальных фаз, называемая фазовым сдвигом. Чаще всего встречается фазовый сдвиг между током и напряжением.
Если
,
то говорят, что напряжение опережает
ток по фазе, при
напряжение отстает по фазе от тока, при
напряжение и ток совпадают по фазе, а
если
,
то напряжение и ток находятся в
противофазе.
Волновые диаграммы не всегда удобны для исследования, особенно при сложных разветвленных цепях. Проще в этом случае изображать синусоидальные величины вращающимися векторами. Предполагается вращение против часовой стрелки с частотой вращения ω.
Векторная форма представления синусоидальной электрической величины – это вращающийся в декартовой системе координат x0y вектор с началом в точке 0, длина которого равна амплитуде синусоидальной величины, угол относительно оси х – её начальной фазе, а частота вращения – ω = 2πf. Проекция данного вектора на ось у в любой момент времени определяет мгновенное значение рассматриваемой величины.
Рис. 2 |
Совокупность векторов, изображающих синусоидальные функции, называют векторной диаграммой, рис. 2
|
Изобразим вращающийся вектор, соответствующий току (рис. 3):
.
Рис. 3 |
Величина вектора ОА в заданном масштабе представляет амплитудное значение Im. Проекция этого отрезка на вертикальную ось y (ОВ) есть мгновенное значение величины i(t) в момент времени t. Любой вектор на плоскости, проведенный из начала координат и изображающий значение ЭДС, напряжения или тока, однозначно определяется точкой, соответствующей концу этого вектора (точка А на рис. 3).
|
Комплексное представление синусоидальных электрических величин сочетает наглядность векторных диаграмм с проведением точных аналитических расчётов цепей.
Ток и напряжение изобразим в виде векторов на комплексной плоскости, (рис. 4). Ось абсцисс называют осью действительных чисел и обозначают +1, ось ординат называют осью мнимых чисел и обозначают +j. (В некоторых учебниках ось действительных чисел обозначают Re, а ось мнимых – Im). Рассмотрим векторы U и I в момент времени t = 0.
Рис. 4
|
Каждому из этих векторов соответствует комплексное число, которое может быть представлено в трёх формах: - алгебраической
где
|
;
,
,
,
,
– проекции векторов на оси действительных
и мнимых чисел.- показательной
;
,
где U, I – модули (длины) векторов;
е – основание натурального логарифма;
и
– поворотные множители, т. к. умножение
на них соответствует повороту векторов
относительно положительного направления
действительной оси на угол, равный
начальной фазе.
- тригонометрической
;
.
При решении задач в основном применяют алгебраическую форму (для операций сложения и вычитания) и показательную форму (для операций умножения и деления). Связь между ними устанавливается формулой Эйлера
.