Г) смешанное соединение

При смешанном соединении построение ВАХ цепи можно произвести поэтапно, используя правила для последовательного и параллельного соединений.

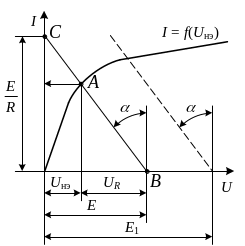
3.2.2 Метод опрокинутой характеристики.

Рассмотрим этот метод на примере последовательного соединения нелинейного элемента НЭ и линейного R (рис. 12). В этом случае нет необходимости строить результирующую ВАХ схемы.

Характеристику нелинейного элемента I = f(U_НЭ) строят обычным образом. Опрокинутая характеристика линейного элемента, представляющая собой прямую линию, может быть построена по двум точкам. Если U_R = 0, то характеристике I_R = f(U_R) принадлежит точка «В», если U_НЭ = 0, то характеристика I_НЭ = f(U_НЭ) пересекает ось ординат в точке «С», определяемой соотношением

.

а)	б)

Рис. 12

Точка пересечения «А» двух графиков даёт решение задачи.

При изменении ЕДС от Е до Е₁ прямую I_R = f(U_R) следует переместить параллельно себе так, чтобы она исходила из точки I = 0. U = E₁ (пунктирная прямая на рис. 12, б).

Или по Бессонову Л.А.

Метод пересечения характеристик (метод опрокинутой характеристики) удобно применять для решения частной задачи, когда один из элементов последовательной цепи является линейным элементом (резистором), заданы ЭДС (или напряжение на зажимах цепи U) и сопротивление R. Требуется определить ток и падения напряжений на элементах цепи.

При расчёте цепи данным способом нет необходимости строить результирующую ВАХ пассивной части схемы. Учитывая, что уравнение

в координатах I и U_нэ представляет собой уравнение прямой, проходящей через две точки:

при U_нэ = 0, , , даст точку «С» на оси ординат;

при I = 0, U_нэ = Е, даст точку «В» на оси абсцисс.

ЛЕКЦИЯ № 3

Тема № 4 анализ и расчёт линейных цепей переменного тока

Учебные вопросы:

4.1 Получение однофазного синусоидального тока. Основные параметры, характеризующие синусоидальную величину: действующее и среднее значения синусоидальных величин и представление их в виде волновых, векторных диаграмм и комплексными числами. Законы Ома и Кирхгофа в комплексной форме.

4.2 Особенности физических процессов в цепях переменного тока, реальные и идеальные элементы. Законы Ома, фазовые соотношения, векторные диаграммы, мгновенная и средняя мощности для простейших цепей синусоидального тока (цепи с резистором, индуктивностью и конденсатором).

Литература:

7. Касаткин а.С., Немцов м.В. Электротехника. – м.: Высшая школа, 2000. – 572 с.

8. Электротехника и электроника: учебное пособие для вузов / в.В.Кононенко [и др.]. Изд. 2-е. – Ростов н/д.: Феникс, 2005. – 752 с.

9. Рекус г.Г. Основы электротехники и электроники в задачах и решениях. – м.: Высшая школа, 2005. – 285 с.

4.1 Получение однофазного синусоидального тока. Основные параметры, характеризующие синусоидальную величину: действующее и среднее значения синусоидальных величин и представление их в виде волновых, векторных диаграмм и комплексными числами. Законы Ома и Кирхгофа в комплексной форме.

Синусоидальным током называют ток, изменяющийся во времени по синусоидальному (гармоничному) закону (рис. 1).

Рис. 1

Синусоидальные токи находят широкое применение в электрических цепях электро-, радио- и других установках. Периодические величины изменяются во времени (i=i(t); u=u(t)) по значению и направлению, причём эти изменения повторяются через некоторые равные промежутки времени Т, называемые периодом (рис.1). .

Период – это время, за которое совершается одно полное колебание.

В любой промежуток времени значение тока i(t) можно определить из выражения

Величину i(t) называют мгновенным значением тока.

Синусоидальный ток характеризуется следующими параметрами:

а) – угловая частота (рад/с или с^–1),

где Т – период колебания (с);

f – частота колебания ( ) (Гц);

б) – амплитудное (максимальное) значение тока (обозначается с индексом m);

в) аргумент синуса, т.е. , называют фазой. Фаза характеризует состояние колебания в данный момент времени t. Величина ψ_i называются начальная фаза.

Любая синусоидальная функция характеризуется темя величинами: амплитудой, угловой частотой и начальной фазой.

В европейских странах в качестве стандартной промышленной частоты принята f = 50 Гц, в США и Японии f = 60 Гц.

Разность начальных фаз двух синусоидальных величин одинаковой частоты ( ) называется сдвигом фаз между ними:

.

Синусоидальный ток имеет ряд преимуществ перед постоянным током, в связи с чем он получил очень широкое распространение:

а) его легко трансформировать из одного напряжения в другие,

б) при передаче на большие расстояния (сотни и тысячи километров) от источника до потребителя при многократной трансформации напряжение остается неизмененным, т.е. синусоидальным,

в) с его помощью может быть достаточно просто получено вращающееся магнитное поле, используемое в синхронных и асинхронных машинах.

Синусоидальные токи и ЭДС сравнительно низких частот, до нескольких килогерц, получают с помощью синхронных генераторов (их изучают в курсе электрических машин). Синусоидальные токи и ЭДС высоких частот получают с помощью ламповых и полупроводниковых генераторов, подробно рассматриваемых в разделе – электроника.