7.2 Основные понятия и законы теории магнитных цепей. Параметры магнитных цепей и связь между ними. Аналоги законов Ома и Кирхгофа для магнитных цепей
Закон полного тока
Одним из основных законов магнитных цепей является закон полного тока, который устанавливает связь между напряжённостью магнитного поля и величиной тока.
Рис. 5 |
На рис. 5 изображены два провода, по которым текут токи I1 и I2. Вокруг токов имеется контур L. (Контур это замкнутая линия, мысленно проведённая вокруг токов). Токи проходят через поверхность, ограниченную контуром L. |
Определение закона полного тока: полный ток – это алгебраическая сумма токов, проходящих через ограниченную замкнутым контуром поверхность.
Ток In, пронизывающий контур L, считается положительным, если направление обхода контура и направление этого тока связаны правилом правоходового винта (буравчика).
В нашем примере полный ток ΣI есть сумма токов I1 и I2:
.
Теперь найдём магнитное напряжение вдоль контура L. Разбиваем контур на отрезки, которые можно считать прямолинейными, а магнитное поле в месте расположения отрезков однородным. Магнитное напряжение Um для одного такого отрезка длиной ΔL:
,
где НL – напряжённость магнитного поля на контуре L.
Магнитное напряжение вдоль всего контура L
.
Полный ток равен магнитному напряжению вдоль контура:
.
Это равенство, установленное экспериментально, и связывает токи с напряжённостью их магнитного поля.
Магнитное напряжение вдоль замкнутого контура часто называют магнитодвижущей силой. Другое название магнитного напряжения вдоль замкнутого контура – намагничивающая сила.
Тогда закон полного тока можно сформулировать так: магнитодвижущая сила F вдоль замкнутого контура L равна полному току ΣI, пронизывающему поверхность, ограниченную данным контуром L.
Формула закона полного тока:
.
Или циркуляция вектора напряженности магнитного поля вдоль замкнутого контура равна алгебраической сумме токов, охватываемых этим контуром
(4)
где Н – напряженность магнитного поля;
l – длина контура;
I – ток.
Законы Ома и Кирхгофа для магнитных цепей
Если имеется несколько витков W с одним и тем же током (катушка), то
,
(5)
где F – намагничивающая сила (НС), это скалярная величина, характеризующая намагничивающее действие тока.
С вектором напряженности Н связан вектор магнитной индукции В
(6)
где 
– абсолютная магнитная проницаемость;
– магнитная постоянная (магнитная
проницаемость вакуума
= 4π×10-7, Г/м – генри на метр);
– относительная магнитная проницаемость.
Эти
величины связаны соотношением
.
В практических расчётах магнитные цепи стараются разбить на минимальное число однородных участков, тогда интеграл можно заменить суммой
,
(7)
где n – число однородных участков.
Если на
участке нет катушек с током, то произведение
вида
называют разностью магнитных потенциалов
между точками m и n
или магнитным
напряжением:
.
В общем случае
.
Поскольку линии магнитной индукции всегда непрерывны и замкнуты в пространстве, то поток вектора магнитной индукции сквозь замкнутую поверхность равен нулю:
,
отсюда следует, что магнитный поток Ф в неразветвленной цепи на всех участках k одинаков, т.е. при разветвлении магнитной цепи поток на участке, подходящем к разветвлению, равен сумме потоков на участках, отходящих от разветвления. Получаем вывод: в разветвленных магнитных цепях магнитные потоки подчиняются первому закону Кирхгофа (но необходимо помнить, что речь идет лишь об аналогии двух принципиально разных явлений).
Если вектор индукции В одинаков во всех точках и перпендикулярен площади сечения участков, то можем записать для k-го участка:
и
откуда получаем
.
подставим в полученное выше выражение:
(8)
получаем аналог закона Ома для магнитной цепи. Здесь RMk – магнитное сопротивление k -го участка:
,
где lk – длина средней линии магнитной индукции, проходящей через центры тяжести сечений.
Можно ввести и магнитную проводимость:
.
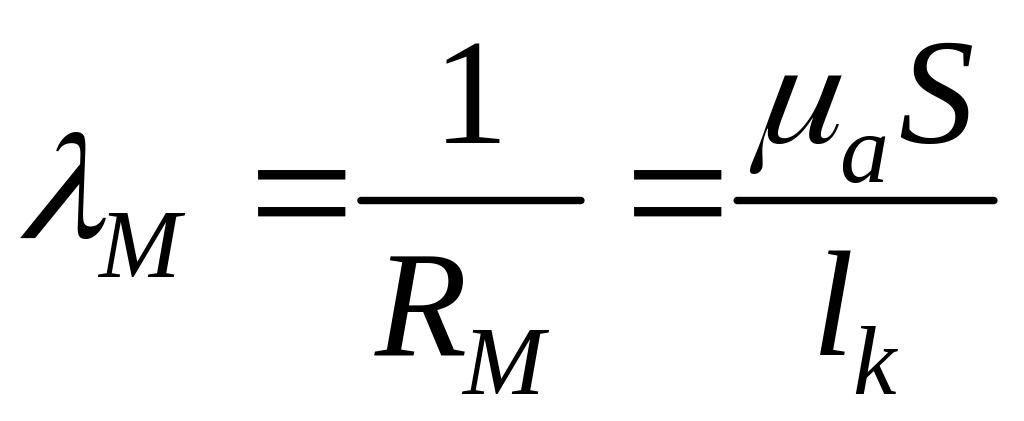Магнитные потоки, напряжения и намагничивающие силы в контурах магнитных цепей подчиняются второму закону Кирхгофа, его аналог для магнитной цепи может быть сформулирован так:
В любом замкнутом контуре магнитной цепи алгебраическая сумма магнитных напряжений равна алгебраической сумме намагничивающих сил, действующих в данном контуре:
.
Более удобная для практики запись:
.