Контрольные вопросы для защиты работы
Основные:
1. Опишите этапы вывода уравнения для потока тепла через цилиндрическую стенку.
2. Каким образом методика данного эксперимента обеспечивает выполнение условия t = t(r) ?
3. Какие материалы имеют коэффициенты теплопроводности, близкиепо порядку величины к измеренным?
4. Перечислите погрешности, связанные с неидеальностьюреализацииметодики определения коэффициента теплопроводности. Назовите наиболеесущественные из них.
5. Перечислите инструментальные погрешности, присущие даннойэкспериментальной установке. Назовите наиболее существенные из них.
Дополнительные:
6. Проанализируйте поведение уравнения для потока тепла через цилиндрическую стенку при устремлении к бесконечности радиуса наружной
стенки. Сформулируйте физическую интерпретацию этого поведения.
7. Перечислите погрешности метода определения коэффициента теплопроводности. Назовите наиболее существенные из них.
8. Пусть измерения проведены до того, как установится стационарныйрежим. Будет ли значение коэффициента теплопроводности, рассчитанное поданным этих измерений, завышенным или заниженным по сравнению с действительным? Обоснуйте ответ.
9. Вам необходимо измерить теплопроводность некоторого материала с
помощью данной лабораторной установки. Каков будет Ваш порядокдействий?
10. Сделайте свои предложения по снижению погрешности определения коэффициента теплопроводности.
Лабораторная работа 2. Определение коэффициента температуропроводноститвердых телметодом регулярного режима
Цель работы: исследование процесса нестационарной теплопроводности на предмете тела, испытывающего охлаждение врегулярном режиме.
Задачи работы: изучение закономерностей временной эволюции температурного поля в твердом теле; определение стадии регулярногорежима вэксперименте с охлаждением тела; расчет теплопроводности и температуропроводности теплоизоляционного материала на основе данных о темпе охлаждения.
1. Теоретические сведения
В общем случае поле температур охлаждаемого или нагреваемого тела
определяется начальным тепловым состоянием тела, его физическими свойствами, геометрической формой и размерами, а также условиями теплообмена с окружающей средой.
По истечении некоторого промежутка времени (при числе Фурье, превышающем 0,3–0,5) устанавливается упорядоченный (регулярный) тепловойрежим, при котором поле температур в теле перестает зависеть от особенностей начального распределения температуры. Если процесс теплообменапроисходит в условиях постоянной температуры среды, окружающей тело, икоэффициент теплоотдачи сохраняет неизменное значение, температура телабудет изменяться во времени по экспоненциальному закону; темп охлаждения (нагревания) для всех точек тела будет иметь постоянное значение.
Математически поле температур тела в регулярном режиме представляется зависимостью
|
(4) |
где θ – избыточная температура, отсчитываемая от температуры окружающей среды; А – постоянный множитель, определяемый из начальных условий; U – функция, зависящая от координат; m – темп охлаждения; τ – время.Темп охлаждения характеризует относительную скорость изменения избыточной температуры.
Условия теплообмена тела с окружающей средой определяются числом
Био.При малой интенсивности теплообмена (Bi< 0,1) темп охлаждения прямо пропорционален коэффициенту теплоотдачи, площади поверхности тела иобратно пропорционален его полной теплоемкости:
|
(4) |
где α – коэффициент теплоотдачи; F – площадь поверхности тела; С– полная теплоемкость тела. При интенсивном теплообмене тела с окружающейсредой (Bi→ ∞) температура поверхности приблизительно равна температуре окружающей среды. В этих условиях температурное поле в теле является суперпозицией бесконечного числа гармоник, каждая из которых экспоненциально убывает со своей скоростью:
У однородного цилиндрического тела радиусом R и длиной l
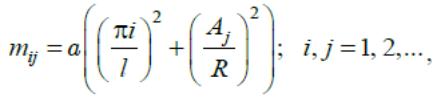
где Aj– j-й нуль функции Бесселя нулевого порядка. Первый нульA1≈ 2,405, второй A1≈ 5,5, далее с ростом j нули функции Бесселя располагаются приблизительно в точках Aj≈ const+ π j . Легко видеть, что из всехгармоник наиболее медленно убывает та, что имеет наименьшие значения i, j:
|
(6) |
По истечении некоторого времени все гармоники, кроме этой, перестанут давать существенный вклад в температурное поле. Градиенты тепла и, следовательно, интегральный поток тепла от тела к окружающей среде станут пропорциональны e−m11τ. Эта стадия нестационарного процесса носит названиерегулярного режима. Определив зависимость от времениизбыточных температур или потоков тепла, мы можем найти величину темпа охлажденияm = m11 и по известным геометрическим параметрам телаопределить еготемпературопроводность. Основную погрешность в методике дает пренебрежение высшими гармониками, которые убывают быстрее, чем основная, номогут все еще влиять на температурное поле. Из высших гармоник, которыенаиболее медленно убывают, i = 2, j =1 и i =1, j = 2. Для них
Удельный вклад высших гармоник можно оценить как
|
(7) |
Основной величиной, которая определяется в опытах, является темпохлаждения. Зависимость (5) позволяет найти коэффициент теплоотдачи, если известна полная теплоемкость. При заданном (найденном из опыта) коэффициенте теплоотдачи по (5) определяется теплоемкость.
Соотношение (6) служит для определения температуропроводности тела при известных параметрах его формы. По найденным значениям теплоемкости и температуропроводности расчетным путем определяют теплопроводность λ =aρc .