4. Проведение расчетов

Из экспериментальных данных определяется величина темпа охлаждения на участке пленочного кипения. Если температура ампулы есть функциявремени t = f (τ), тогда

где ϑ_τ = t_τ − t_s, t_s=100 °C; t_τ – температура ампулы (в градусах Цельсия) вмомент времени τ.

Нагретая ампула погружается в кипящую воду на глубину 10 – 35 мм взависимости от того, какой продолжительности должен быть эксперимент.Величина глубины погружения определяет площадь поверхности теплообмена, а соответственно, и интенсивность отвода тепла от образца. Если h – глубина погружения образца, тогда площадь поверхности теплообмена складывается из двух составляющих:

F = F₁+F₂,

где F₁= π⋅d₁⋅h;F₂= 0,25⋅ π⋅d₂; d – внешний диаметр ампулы (25 мм)(индексом 1 обозначена поверхность, образованная боковой поверхностьюампулы, погруженной на глубину h, а индекс 2 соответствует поверхностидна ампулы).

На участке пленочного кипения темп охлаждения сохраняется постоянным вне зависимости от выбранных моментов времени τ₁ и τ₂.Удельные теплоемкости материалов ампулы равны:

для меди

c_p= 390Дж/(кг ⋅К);

для стали

c_p= 510Дж/(кг ⋅К).

Масса меди составляет 200 г, стали – 75 г.

Экспериментальное значение коэффициента теплоотдачи находится поформуле

гдеС– полная теплоемкость ампулы; ψ – коэффициент неравномерностираспределения температур в теле, принимает значения от 0 до 1. Посколькутермическое сопротивление пленки пара много больше, чем у составляющихампулы, то можно принять (ψ = 1). Из-за малости рабочего участка в даннойустановке реализуется ламинарное течение паровой пленки.

Базируясь на предположении, что толщина паровой пленки есть толщина пограничного слоя и решая уравнения стационарной теплопроводности, для ламинарного движения пленки Нуссельтом была получена теоретическая формула для нахождения коэффициента теплоотдачи:

где

λ_п – теплопроводность пара (при р = 1 бар λ_П = 2,372⋅10^-2 Вт/(м·К));

ν_п – кинематическая вязкость пара (при р = 1 бар ν_п = 20,02⋅10^-6 м²/с);

r – удельная теплота парообразования (при р= 1 бар r = 2256,8 кДж/кг);

g – ускорение свободного падения (9,80 м/c²);

ρ_п – плотность насыщенного пара (при р = 1 бар ρ_п = 0,598 кг/м³);

ρ_ж – плотность насыщенной жидкости (при р= 1 бар ρж = 958,4 кг/м³);

l₀ – характерный размер поверхности теплообмена (в случае дна l₀ = d;в случае боковой поверхности l₀ = h);

С_н – поправочный коэффициент на расположение поверхности (вслучае горизонтальной поверхности С_н = 0,72, в случае вертикальнойС_н=0,943);

Δt – разница температур между поверхностью теплообмена и жидкостью, в которую она погружена:

Δt= t_c− t_s,

где t_с можно (учитывая малую толщину стенки ампулы) в первомприближении принять равной температуре на её внутренней поверхности.

t_c= t_внеш,

где t_внеш – температура внешней термопары, заключенной между меднойболванкой и стальным корпусом.

Чтобы найти средний коэффициент теплоотдачи по всей поверхностиампулы, необходимо сложить теплоотдачи по поверхностям, предварительносоотнося их к долям этих поверхностей от общей поверхности ампулы:

Получившиеся результаты не должны расходиться более чем на 5 %.

Для оценки величины плотности теплового потока используется соотношение

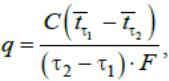
где изменение температур во времени на коротком участке можно описатьлинейными функциями

индексы «внутр» и «внеш» соответствуют термопарам, заключенным в центре и на поверхности медной болванки.

Вторая критическая плотность теплового потока экспериментальнооценивается следующим образом. Температура предельного перегрева жидкости, как и температура насыщения, является функцией только давления:

t_пр= 300 + 0,33(p −1),

где p – давление в барах.

По найденной температуре предельного перегрева жидкости оценивается величина критического температурного напора:

Δt_кр2= 0,9(t_пр− t_s).

После этого по закону Ньютона – Рихмана можно записать:

q_кр2= α_кр2Δt_кр2,

где α_кр2соответствует значению коэффициента теплоотдачи, полученномув результате эксперимента. При необходимости полученный результат можно сравнить с теоретическим соотношением, полученным С. С. Кутателадзе:

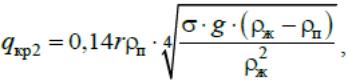
где σ – коэффициент поверхностного натяжения (при нормальном давленииσ=5,886⋅10^–2 Н/м).