2.4 Расчет поперечного ребра

Поперечное ребро рассматривается как балка на двух свободных опорах с расчетным пролетом, равным расстоянию между осями продольных рёбер l_eff=2,18-0,1=2,08м (рис 2.4в).

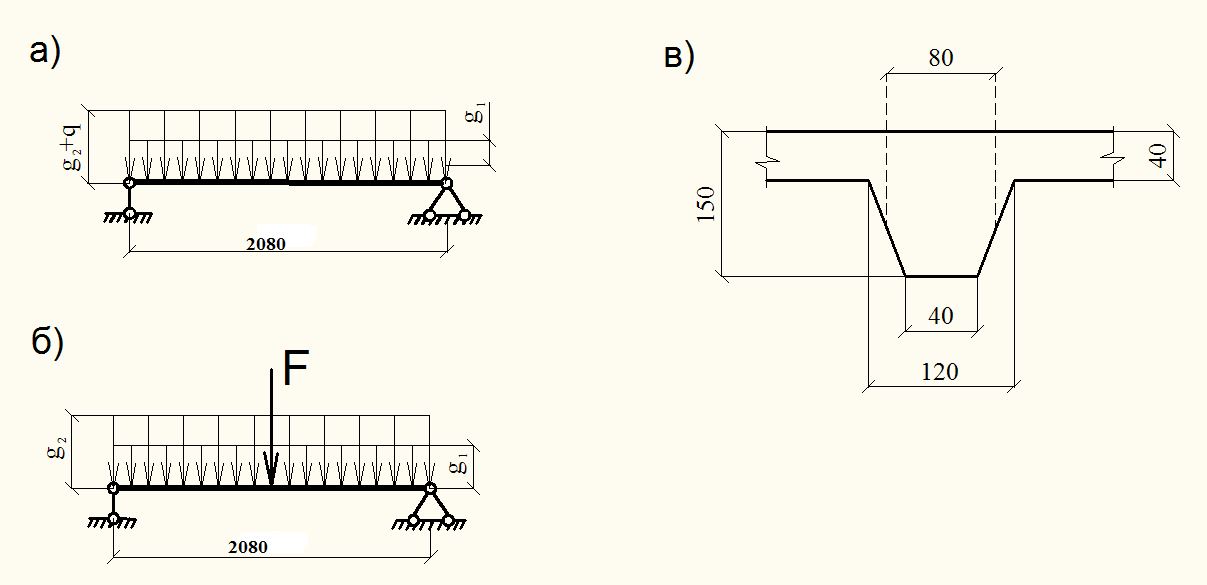
Рисунок 2.4 - Расчетные схемы и сечение поперечного ребра

Расчетная схема ребра при действии постоянной и снеговой нагрузок приведена на рис.2.4а;

Постоянная расчетная нагрузка на ребро:

- от собстенного веса ребра (без учета полки)

g₁=0,08·0,11·2500·10·1·1,35=297Н/м=0,297кН/м

- передаваемая полкой плиты

g₂=2,29·1,5=3,206 кН/м

- расчетная снеговая нагрузка на ребро

g_sd=1,5·1,9=2,16 кН/м

Расчетный изгибающий момент в пролете:

М_sd=((g₁+g₂+g_sd)·l_eff²)/8 (12)

М_sd=((0,297+3,206+2,25)·2,88²)/8= 3,03 кН·м.

Поперечная сила у опор:

V_sd=(( g₁+g₂+g_sd) ·l_eff)/2 (13)

V_sd=(( 0,297+3,206+1,68)·2,25)/2=5,83 кН

Расчетные усилия в ребре от постоянной нагрузки и сосредоточенной от веса рабочего с инструментом F_sd=1·1,5=1,5 кН (рис 2.4б)

М_sd=((g₁+g₂)·l_eff²)/8+(F_sd·l_eff)/5 (14)

М_sd=((0,297+3,2)·2,08²)/8+(1,5·2,08)/5= 2,52 кН·м.

V_sd=(( g₁+g₂)·l_eff)/2+F_sd (15)

V_sd=(( 0,297+3,206)·2,08)/2+1,5=5,143 кН.

Наиболее невыгодной по изгибающему моменту и поперечной силе является 1-ая комбинация нагрузок.

Ребро армируется одним плоским каркасом. Рабочая арматура стержневая класса S500 (f_yd=435 МПа).

Ширину полки тавра определяем по формуле:

b_f′=b_sb+2·b_свеса, (16)

где b_свеса- ширина свеса, которая не должна превышать 1/6·l_eff=1/6·2,08=0,35 м

В принятом ранее сечении b_свеса=(1,5-0,08)/2= 0,88 м > 0,35 м, поэтому в расчет принимаем b_свеса=350 мм.

b_f′=80+2·350=780 мм.

Расчетную рабочую высоту сечения d определяем с учетом толщины защитного слоя и половины диаметра рабочей арматуры (принимая во внимание указания табл.11.4 [1, изм. 3], ориентировочно примем с=30мм):

d=h-c=150-30=120 мм.

Предполагая, что нейтральная ось проходит по нижней грани полки, определяем область деформирования для прямоугольного сечения шириной b_f′=1040 мм и положение нейтральной оси при расчете тавровых сечений:

(17)

Для арматуры S500 при Е_s=2·10⁵ МПа ‰

что указывает на то, что сечение находится в области деформирования II [5, таб.6.7] , для которой .

Проверим выполнение условия:

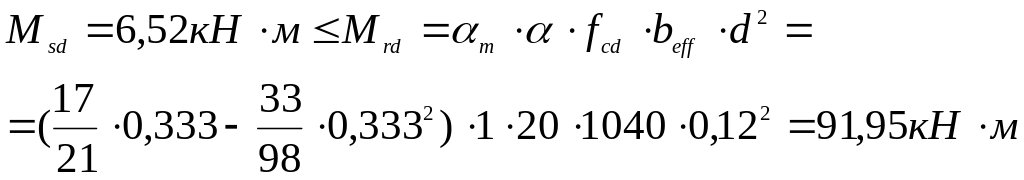
Условие выполняется, т.е. нейтральная ось проходит в полке и расчетное сечение – прямоугольное с шириной b_f′=1040 мм .

Тогда

Определяем значение коэффициента α_m:

α_m =3,03·10³/1·20·10^-3·780·120²)=0,013< α_m,lim=0,371.

Т.к. α_m< α_m,lim, то арматура в сечении используется полностью. Далее определяем значение коэффициента η:

Требуемая площадь растянутой арматуры:

A_st=M_sd/(f_yd·η·d)=3,03·10⁶/(435·0,993·120)=58,45 мм².

Принимаем 1⌀12 мм S500 площадью 113,1 мм².

Прочность железобетонных элементов на действие поперечных сил при отсутствии поперечной арматуры, согласно требованиям норм [1], проверяем по условию:

V_sd≤V_Rd,ct,

где V_sd– расчетная поперечная сила от внешних воздействий;

V_Rd,ct– поперечная сила, воспринимаемая железобетонным элементом без поперечного армирования.

Находим поперечную силу, воспринимаемую железобетонным элементом без поперечного армирования:

V_rd,ct=(0,12 ·k·(100·ρ·f_ck)^⅓-0,15·σ_ср)·b_sb·d, (18)

где (19)

Принимаем k=2.

ρ – коэффициент армирования;

ρ=A_st/(b_w·d)≤0,02 (20)

ρ=113,1/(80·120)=0,012<0,02.

σ_ср– напряжения в бетоне, вызванные наличием осевого усилия, σ_ср=0.

V_rd,ct=(0,12·2·(100·0,012·30)^⅓-0,15·0)·80·120·10^-3=7,61 кН.

Но не менее V_Rd,ct,min=(0,4∙f_ctd-0,15∙σ_ср)∙b_w∙d, (21)

V_Rd,ct,min=(0,4∙1,33)∙0,08∙0,12·10³=5,11 кН.

Поскольку V_sd=5,83 кН>V_Rd,ct=7,61 кН, поперечную арматуру необходимо устанавливать по расчету.

Проверяем условие обеспечения прочности по наклонной полосе между наклонными трещинами:

V_Sd ≤ V_Rd,max , (22)

где V_Rd,max должно быть в пределах:

V_Rd,max = 0,3· η_w1 · η_c1 · ƒ_cd · b_w ·d, (23)

где

η_w1-коэффициент, учитывающий влияние поперечной арматуры, нормальной к продольной оси элемента,

η_w1=1+5·α_E·ρ_sw≤1,3 (24)

α_E- коэффициент перехода от арматуры к бетону,

α_E=Е_s/ Е_c, (25)

где Е_s- модуль упругости арматуры, Е_s=2·10⁵ МПа

Е_c- модуль упругости бетона, Е_c=36,9·10³ МПа(см. п.2.1)

α_E=2·10⁵/(36,9·10³)=5,42

ρ_sw- коэффициент армирования поперечной арматурой,

ρ_sw=A_sw/(b_w·S) (26)

A_sw- площадь поперечной арматуры, пересекаемая наклонной полосой бетона,

b_w- минимальная ширина поперечного сечения элемента в растянутой зоне,

ρ_sw=28,3/(80·150)=0,0024

Подставляем найденные значения α_E и ρ_sw в формулу (24):

η_w1=1+5·5,42·0,0024=1,07<1,3

η_с1=1-β₄·ƒ_cd, (27)

β₄=0,01- для тяжелых бетонов.

η_с1=1-0,01·20=0,8.

Проверяем условие (22), подставив найденные значения:

V_Rd,max = 0,3· 1,07 · 0,8 · 20 · 80 ·120=49,31 кН.

V_sd=5,83 кН< V_Rd,max = 49,31 кН.

Следовательно, диаметр хомутов и их шаг выбраны верно.

Теперь необходимо произвести расчет поперечного ребра с поперечной арматурой по наклонной трещине.

Вычисляем поперечную силу, которую могут воспринимать бетон и поперечная арматура:

, (28)

где η_с2=2 - для тяжелых бетонов;

η_f - коэффициент, учитывающий влияние сжатых полок в тавровых и двутавровых элементах:

η_f=0,75·( b_f´ - b_w) ·h_f´ /( b_w·d) ≤0,5 (29)

причем должно выполняться условие:

b_f - b_w≤3·h_f´ (30)

b_f - b_w=780-80=700>3·h_f´=3·40=120

Условие не выполняется, поэтому вместо ( b_f´ - b_w) вводим в расчет 3·h_f=120 мм.

η_f=0,75·120·40/( 80·120) =0,375≤0,5 ;

η_N- коэффициент,учитывающий влияние продольных сил, η_N =0;

Находим линейное усилие, которое может воспринять поперечная арматура:

V_sw=a_sw·n_w·f_ywd / S_w , (31)

где a_sw- площадь поперечного сечения стержня Ø 6 мм,

n_w- количество пересекаемых наклонной полосой бетона стержней поперечной арматуры,

f_ywd =174 МПа–расчетное сопротивление поперечной арматуры [1,изм.4, таб.6.5],

S_w- шаг хомутов.

V_sw=28,3·1·174/150=32,83Н/мм

Подставляя найденные значения в формулу (28), находим значение V_rd:

=23,55 кН.

Поперечная сила, которую могут воспринять хомуты и бетон V_sd=9,05 кН<V_rd=23,55 кН, следовательно прочность наклонных сечений обеспечена.

Среднее поперечное ребро высотой 250 мм рассчитывается аналогично.

Постоянная расчетная нагрузка на ребро:

- от собстенного веса ребра (без учета полки)

g₁=0,08·0,21·2500·10·1·1,35=567Н/м=0,567 кН/м

- передаваемая полкой плиты

g₂=2,29·1,5=3,43 кН/м

- расчетная снеговая нагрузка на ребро

g_sd=1,5·1,5=2,25 кН/м

Расчетный изгибающий момент в пролете:

М_sd=((g₁+g₂+g_sd)·l_eff²)/8=((0,567+3,43+2,25)·2,08²)/8= 3,38 кН·м.

Поперечная сила у опор:

V_sd=(( g₁+g₂+g_sd) ·l_eff)/2=(( 0,567+3,43+2,25)·2,08)/2=6,49 кН

Расчетные усилия в ребре от постоянной нагрузки и сосредоточенной от веса рабочего с инструментом F_sd=1·1,5=1,5 кН

М_sd=((g₁+g₂)·l_eff²)/8+(F_sd·l_eff)/5=((0,567+3,43)·2,08²)/8+(1,5·2,08)/5= 2,78 кН·м.

V_sd=(( g₁+g₂)·l_eff)/2+F_sd =(( 0,567+3,43)·2,08)/2+1,5=5,66 кН.

Наиболее невыгодной по изгибающему моменту и поперечной силе является 1-ая комбинация нагрузок.

Ребро армируется одним плоским каркасом. Рабочая арматура стержневая класса S500 (f_yd=435 МПа).

Определяем ширину полки.

В принятом ранее сечении b_свеса=(1,5-0,08)/2= 0,88 м > 1/6·l_eff=1/6·2,08=0,35 м, поэтому в расчет принимаем b_свеса=350 мм.

b_f′=80+2·350=780 мм.

Рабочая высота сечения:

d=h-c=250-30=220 мм.

Предполагая, что нейтральная ось проходит по нижней грани полки, определяем область деформирования для прямоугольного сечения шириной b_f′=1040 мм и положение нейтральной оси при расчете тавровых сечений:

что указывает на то, что сечение находится в области деформирования Ib [5, таб.6.7] , для которой .

Проверим выполнение условия:

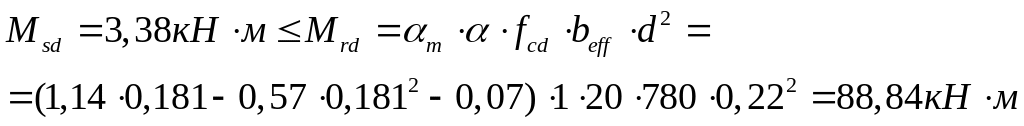
Условие выполняется, т.е. нейтральная ось проходит в полке и расчетное сечение – прямоугольное с шириной b_f′=780 мм .

Тогда

Определяем значение коэффициента α_m:

α_m =3,38·10³/1·20·10^-3·780·220²)=0,044< α_m,lim=0,371.

Т.к. α_m< α_m,lim, то арматура в сечении используется полностью. Далее определяем значение коэффициента η:

Требуемая площадь растянутой арматуры:

A_st=M_sd/(f_yd·η·d)=3,38·10⁶/(435·0,977·220)=36,15 мм².

Принимаем 1⌀8 мм S500 площадью 50,3 мм².

Прочность железобетонных элементов на действие поперечных сил при отсутствии поперечной арматуры, согласно требованиям норм [1], проверяем по условию:

V_sd≤V_Rd,ct,

Находим поперечную силу, воспринимаемую железобетонным элементом без поперечного армирования:

.

Принимаем k=1,95.

ρ=A_st/(b_w·d)≤0,02=50,3/(80·220)=0,0028<0,02.

V_rd,ct=(0,12·k·(100·ρ·f_ck)^⅓-0,15·σ_ср)·b_sb·d=(0,12·2·(100·0,003·30)^⅓-

-0,15·0)·80·220·10^-3=8,79 кН.

Но не менее V_Rd,ct,min=(0,4∙f_ctd-0,15∙σ_ср)∙b_w∙d=(0,4∙1,33)∙0,08∙0,22·10³=9,36 кН.

Поскольку V_sd=6,49 кН<V_Rd,ct=9,36 кН, поперечная арматура устанавливается конструктивно. Принимаем с учетом технологии точечной сварки поперечную арматуру из проволоки Ø6 S240 с шагом 150 мм.