2.2.4 Расчет прочности плиты по нормальному сечению

Расчет продольного ребра плиты

Плиту рассматриваем как свободно лежащую на двух опорах балку П-образного поперечного сечения. Приводим действительное сечение плиты к эквивалентному тавровому сечению высотой 450мм, высотой полки 30мм, шириной 2180мм. Ширина ребра b =(100+150)∙2/2=250мм.

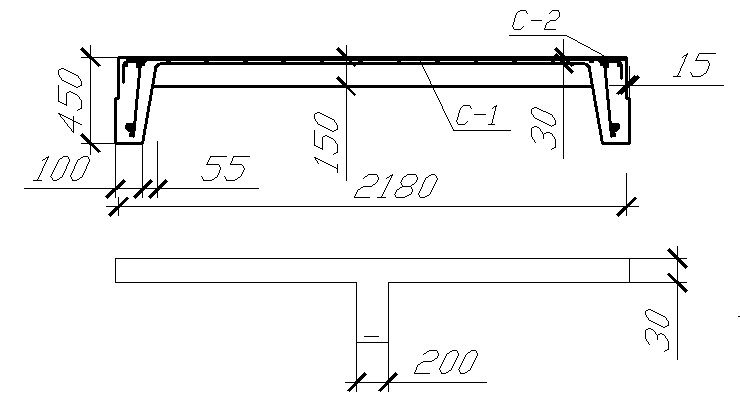Рис.10 – Приведенное сечение плиты

Расчетный пролет плиты:

Где l ­­­­– конструктивная длина плиты,

b_ОП – ширина площадки опирания.

Усилия от расчетных и нормативных нагрузок:

- от расчетной нагрузки

- от нормативной нагрузки (полной)

-от постоянной и длительно действующей

Определим рабочую высоту сечения

При отсутствии напрягаемой арматуры в сжатой зоне:

По справочным данным

нейтральная линия проходит в пределах полки.

Определим граничную высоту сжатой зоны бетона:

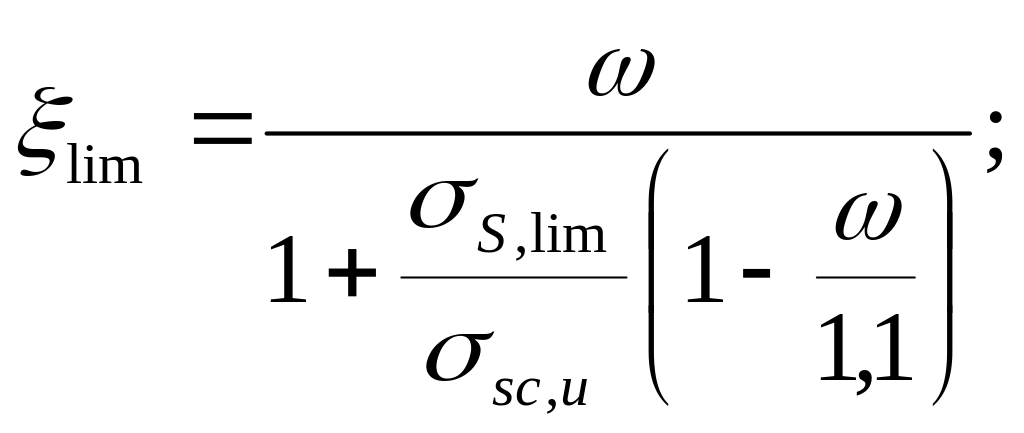
где - характеристика сжатой зоны бетона,

k_о – коэффициент, принимаемый для тяжелого бетона 0,85;

- напряжение в арматуре растянутой зоны;

- предельное напряжение в арматуре сжатой зоны; =500МПа;

При и при , т.е. 0,5∙0,53=0,28>0,05, допускается принимать

Вычисляем площадь сечения растянутой арматуры:

η= 0,983 определяется по таб.20[3].

Принимаем 218 S800 с A_р1  509мм ².

Расчет по наклонному сечению продольного ребра

Поперечную арматуру принимаем класса S240

Необходимо, чтобы выполнялось условие:

,

где

; ;

расчетное сопротивление бетона растяжению;

Получаем:

.

Находим линейное усилие, которое могут воспринять хомуты

где расчетное сопротивление поперечной арматуры;

S – шаг хомутов;

площадь сечения хомутов.

Получаем:

Так как, ,то условие выполняется, следовательно, прочность наклонных сечений обеспечена и поперечной арматуры по расчету не требуется.

2.3 Расчет полки плиты

Расстояние между осями поперечных ребер равно 1400 мм.

Полка представляет собой многопролетную конструкцию с наибольшими размерами поля:

l₁ = 1500 – 2  80 = 1340 мм,

l₂ = 2180 – 2  100 = 1980 мм.

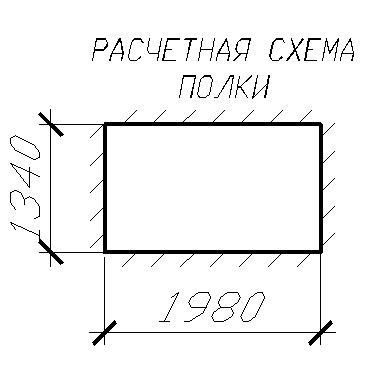
Рисунок 4 - Расчетная схема полки

Соотношение сторон:

l₂ / l₁= 1980 / 1340 = 1,48.

Т.к. l₂ / l₁ = 1,48 < 2, расчетную модель полки ребристой панели принимаем в виде плиты (одной ячейки рассматриваемой ребристой плиты) с защемлением по четырем сторонам (в рёбрах).

На этом основании рассматриваемую плиту целесообразно армировать сеткой с рабочей арматурой вдоль обоих пролетов.

Таблица 2 – Нагрузки на полку плиты (на 1м²)

Вид нагрузки	Нормативная нагрузка кН/м²	Коэфф. надёжности по нагрузке	Расчётная нагрузка кН/м²
1 - нагрузка от веса покрытия без учета веса плиты	0,95	1,3	1,282
2 - вес полки плиты шириной 1м	0,75	1,35	1,012
Итого: постоянная	1,7	-	2,06
временная	1	1,5	1,5
В т. ч. длительная	0,3	1,5	0,45
кратковременная	0,7	1,5	1,05
полная	2,7	-	3,34

Рассчитываем плиту методом предельного равновесия (кинематический способ) [6, парагр.4].

Плита рассматривается в состоянии предельного равновесия как система плоских звеньев, соединенных между собой по линии излома пластическими шарнирами, возникающими в пролетах снизу - по биссектрисам углов, на опорах сверху - вдоль балок, в середине пролета – вдоль длинной стороны плиты.

Воспользуемся готовой формулой [6, формула (3.30)], выведенной из условия равенства работ внешней нагрузки и внутренних усилий на возможных перемещениях:

Fl₁²(3l₂-l₁)/12=(2M₁+M₃+M₄) l₂+(2M₂+M₅+M₆) l₁, (7)

где F – полная нагрузка на полку плиты,

М₁,М₂,М₃,М₄,М₅,М₆ – моменты на 1 п.м. ширины плиты (рис.2.3).

Значения этих моментов находим, пользуясь рекомендуемыми соотношениями между расчетными моментами согласно [6, таб.3.7].

М₂/М₁=0,4

М₃/М₁= М₄/М₁=1,6

М₅/М₁= М₆/М₁=0,6

Подставляя данные значения в формулу (7), получим:

3,341,34²(31,98-1,34)/12=(2M₁+1,6M₁+1,6M₁)1,98+(20,4M₁+0,6M₁+0,6M₁) 1,34;

2,29=10,296M₁ +2,68* M₁;

M₁=0,177 кН/м.

М₂= 0,1770,4=0,07 кН/м,

М₃= М₄=0,1,771,6=0,283 кН/м,

М₅= М₆=0,1770,6=0,106 кН/м.

Арматуру рассчитываем по вычисленным значениям моментов как для изгибаемых элементов прямоугольного сечения.

Используя упрощенный деформационный метод расчета сечений, в качестве расчетного момента выбираем наибольший из действующих вдоль каждой стороны плиты.

Подберем рабочую арматуру, которая будет располагаться параллельно поперечным рёбрам плиты для полосы шириной 1 м. Вычисляем значение коэффициента α_m :

α_m = M_sd / (α · f_cd · b · d²). (8)

Расчетную рабочую высоту сечения d определяем с учетом толщины защитного слоя и половины диаметра рабочей арматуры (принимая во внимание указания табл.11.4 [1, изм. 3], ориентировочно примем с = 17 мм):

d = h – c = 40 – 17 = 23 мм.

α_m =0,164·10⁶/1·16,6·1000·23² =0,012.

Сравниваем полученное значение с α_m,lim:

α_m,lim = ω_с· (ε_cu/( ε_sy+ ε_cu))·(1- k₂· (ε_cu/( ε_sy+ ε_cu))) , (9)

ε_sy = f_yd / Е_s= 417 / 2·10⁵ = 2,085·10^-3,

α_m,lim = 0,81·(3,5 / (2,085+3,5))·(1-0,416·(3,5 / (2,085+3,5))) = 0,375,

α_m = 0,016 < α_m,lim = 0,375 => растянутая арматура достигла предельных деформаций.

Определяем относительное плечо пары сил η:

; (10)

Требуемая площадь сечения растянутой арматуры

A_st1=M_sd/η· f_yd·d;

A_st1=0,106·10⁶/0,993·417·23=11,29 мм² .

Минимальная площадь рабочей арматуры назначаем с учетом коэффициента армирования ρ_min [1, изм.3, таб.11.1]:

ρ_min =26· ≥0,13,

ρ_min =26· > 0,13.

Принимая ρ_min =0,15%, получим:

A_s,min= ρ_min·b·d (11)

A_s,min =0,0015·1000·23=34,5 мм² .

A_s,min=34,5 мм² > A_st1=11,29 мм² , принимаем A_st1=34,5 мм².

С учетом конструктивных требований (шаг S≤200мм) принимаем 5Ø4 мм общей площадью 62,8 мм² с шагом 200 мм.

Аналогично подберем рабочую арматуру, которая будет располагаться параллельно продольным рёбрам плиты:

α_m =0,283·10⁶/1·20·1000·23²=0,032,

α_m=0,041<α_m,lim=0,375

A_st2=0,283·10⁶/0,983·417·23=30,02 мм² .

A_s,min=34,5 мм² > A_st2=30,02 мм² .

С учетом конструктивных требований (шаг S≤200мм) принимаем 5Ø4 мм общей площадью 62,8 мм² с шагом 200 мм.

Назначаем сетку С-1 из проволоки класса S500 Ø4мм с шагом S=200 мм продольных стержней и с шагом S=200 мм поперечных стержней (22 продольных стержней и 45 поперечных).