5. Расчет размерных цепей вероятностным методом

5.1. Основные расчетные зависимости

При расчете размерных цепей методом полной взаимозаменяемости (максимума-минимума)предполагается, что в процессе обработки или сборке возможно одновременное сочетание наибольших увеличивающих и наименьших уменьшающих размеров или обратное их сочетание. Оба случая дают меньшую точность замыкающего звена, но они маловероятны, так как отклонения размеров в основном группируются около середины поля допуска и сочетания деталей с такими отклонениями происходят наиболее часто. Если допустить ничтожно малую вероятность (например, 0,27%) несоблюдения предельных значений замыкающего размера, то можно значительно расширить допуски составляющих размеров и тем самым снизить себестоимость изготовления деталей. На этих положениях и основан теоретико-вероятностный метод расчета размерных цепей.

В теории размерных цепей наиболее часто применяются следующие законы рассеяния размеров деталей: нормальный (закон Гаусса), закон равной вероятности, закон треугольника и закон Максвелла.

Для получения основных расчетных зависимостей вероятностного метода используют теоремы о математических ожиданиях и дисперсиях.

Полагая, что погрешности составляющих и замыкающего размеров подчиняются закону нормального распределения, а границы их вероятного рассеяния (6 ) совпадают с границами полей допусков, можно принять , . При этом у 0,27% деталей размеры замыкающих звеньев могут выходить за пределы поля допуска.

Уравнение для определения допуска замыкающего размера имеет вид:

(16)

Формула (16) выведена из предположения, что распределение действительных размеров подчиняется закону Гаусса, центр группирования совпадает с серединой поля допуска ( ), а поле рассеяния – с величиной допуска.

При несимметричных законах распределения центр группирования не совпадает с серединой поля допуска (рис. 5). Координата центра группирования ( ) для несимметричного закона распределения определяется по выражению:

(17)

где - коэффициент относительной асимметрии несимметричной кривой распределения отклонений -го размера.

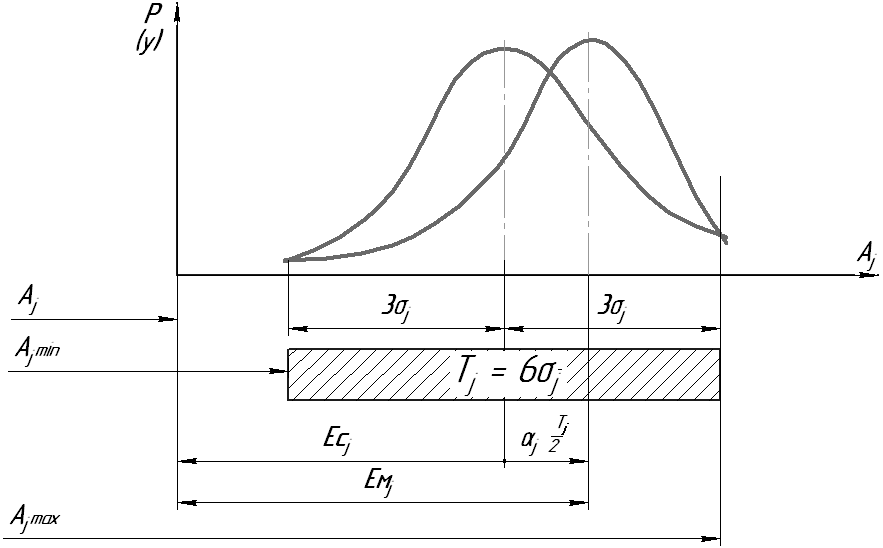
Рис. 5 – Схема определения центра группирования для несимметричной

кривой распределения

Значение координаты середины поля допуска замыкающего звена при асимметричных кривых распределения составляющих размеров определяется по выражению:

, (18)

где и - коэффициенты относительной асимметрии для замыкающего и составляющих звеньев.

Для нормального закона распределения =0.

Для определения допуска замыкающего звена по любому закону распределения погрешностей в формулу (16) вводят коэффициент относительного рассеяния ( )

, (19)

где и - коэффициенты относительного рассеяния замыкающего и составляющих звеньев.

Коэффициент относительного рассеяния , являющийся относительным средним квадратичным отклонением, равен

(20)

Для закона нормального распределения при

;

Когда имеет место закон равной вероятности . При законе распределения, близком к закону Симпсона (закону треугольника), .

Рассеяние размеров замыкающего звена часто можно считать подчиняющимся нормальному закону, для которого .

Тогда выражение (19) примет вид

. (21)

При нормальном законе рассеяния размеров замыкающего звена 99,73% размеров этого звена заключены в пределах поля допуска, т.е. процент риска Р составляет 0,27. Если для каких-либо конкретных условий производства допустим иной выход размера замыкающего звена за пределы его допуска, то последний подсчитывается по формуле:

, (22)

где - коэффициент, зависящий от процента риска Р и принимаемый по табл. 3.

Таблица 3

Значение коэффициента для различных процентов риска Р

Р,%	0,01	0,05	0,1	0,27	0,5	1	2	3	5	10	32
	3,89	3,48	3,29	3	2,81	2,57	2,32	2,17	1,96	1,65	1

5.2. Прямая задача

При решении этой задачи допуск замыкающего звена распределяют между составляющими звеньями цепи различными способами, добиваясь выполнения неравенства:

. (23)

При способе равных допусков средний допуск составляющих звеньев вычисляют по формуле:

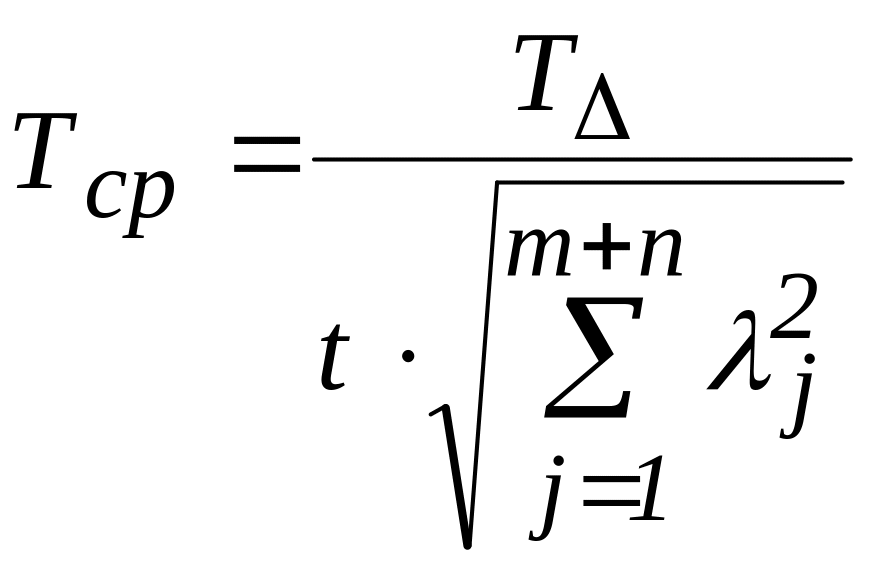. (24)

При способе одной степени точности (квалитета) средний коэффициент точности получают из формулы (22) при условии

, (25)

где - единица допуска размера, принимаемая по табл. 1.

Найденное значение сопоставляют с числом единиц по квалитетам (табл. 2) и определяют квалитет для составляющих звеньев.

По определенному таким образом квалитету и номинальным размерам звеньев назначают допуски на эти звенья и корректируют их, чтобы выполнялось выражение (23).

Предельные отклонения ( и ) назначают по правилу, изложенному в пункте 4.2.2. Координаты середин полей допусков замыкающего ( ) и составляющих ( ) звеньев определяют по формуле (5) и проверяют выполнение равенства (18).

Допускается одно звено принимать за увязочное и для него из равенства (18) определять координату середины поля допуска, а затем по формулам (8) и (9) – предельные отклонения.

5.3. Обратная задача

Последовательность решения обратной задачи вероятностным методом аналогична изложенной в пункте 4.3 для метода полной взаимозаменяемости.

После определения номинального размера замыкающего звена ( ) по уравнению (1), определяют величину допуска по выражениям (19) или (22).

Координату середины поля допуска определяют по формуле (18) и далее вычисляют предельные отклонения ( и ) по выражениям (6) и (7), предварительно подсчитав координаты середин полей допусков всех составляющих звеньев цепи по формуле (5).