3.1 Расчёт нагрузок

Площадь поперечного сечения балки составля­ет:

Нагрузка от веса 1 м длины балки 0,2812·2500 = 7,03 кН/м.

Подсчет равномерно распределенной нагрузки на балку для расчета по предельным состояниям первой группы сведен в таблицу.

Таблица 3.1 Сбор нагрузок на 1м балки.

Вид нагрузки	Нормативная нагрузка кH/м²	Коэфф. надёжности по нагрузке	Расчётная нагрузка кH/м²
Постоянная от веса:
Собственный вес балки	12,6	1,35	17,01
Вес покрытия	16,98	1,35	22,92
Вентиляцион. короба и трубопроводы	4	1,35	5,4
Всего от постоянной нагрузки:	33,58	-	45,33
Временная от снега:	1,2	1,5	1,8
Полная:	34,78	-	47,13

3.2 Определение изгибающих моментов и поперечных сил

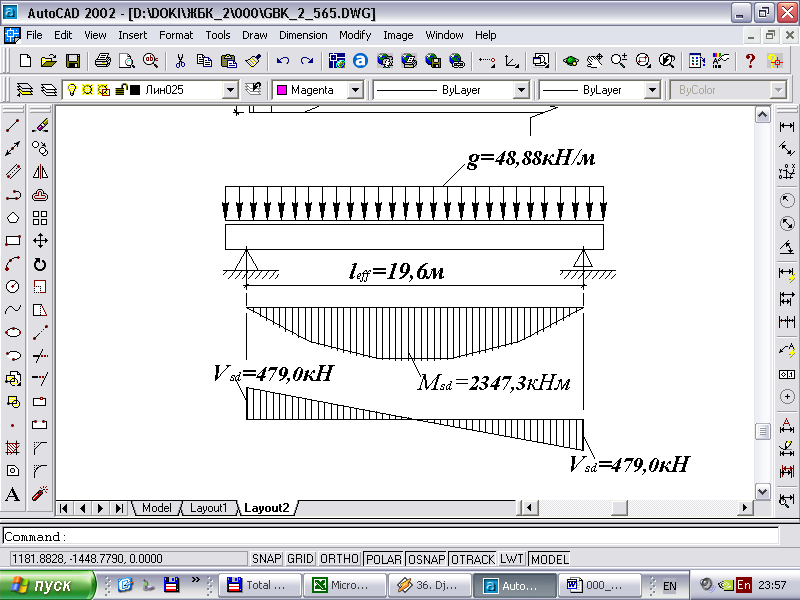
Рисунок 3.2 – Расчётная схема балки и эпюры M_sd и V_sd.

Наибольший изгибающий момент в середине пролета от расчетной нагрузки для предельных состояний первой группы

кНм.

Наибольшая поперечная сила от расчетной нагрузки для пре-

дельных состояний первой группы

кН.

3.3 Предварительное назначение сечения арматуры

Значение предварительного напряжения σ_о арматуры в виде прядей класса 15S1400 может быть назначено из условия: σ_о=р<0,8f_pk. При механическом способе натяжения р=0,05σ_о.

Следовательно, σ_о<0,76 f_pk. Принято:

σ_о=0,7 f_pk = 0,7·16500 = 115,5кН/см²

Ориентировочно сечение напрягаемой арматуры из условия трещиностойкости может быть определено по формуле

A_p ≈

Коэффициент β=0,55.

A_p =

Необходимое число прядей при площади сечения одной пряди 1_,415см² равно 27,07/1,415=19,13. Принимаем 19 прядей класса 15S1400, площадь сечения которых A_ser = 26,89см².

Ориентировочное сечение арма­туры из условия прочности может быть получено по формуле

A_p > ,

что меньше полученного выше значения из условия трещиностойкости. Поэтому для дальнейших расчетов принята напрягаемая арматура из 20 прядей класса 15S1400, размещение которой в балке показано на рис.

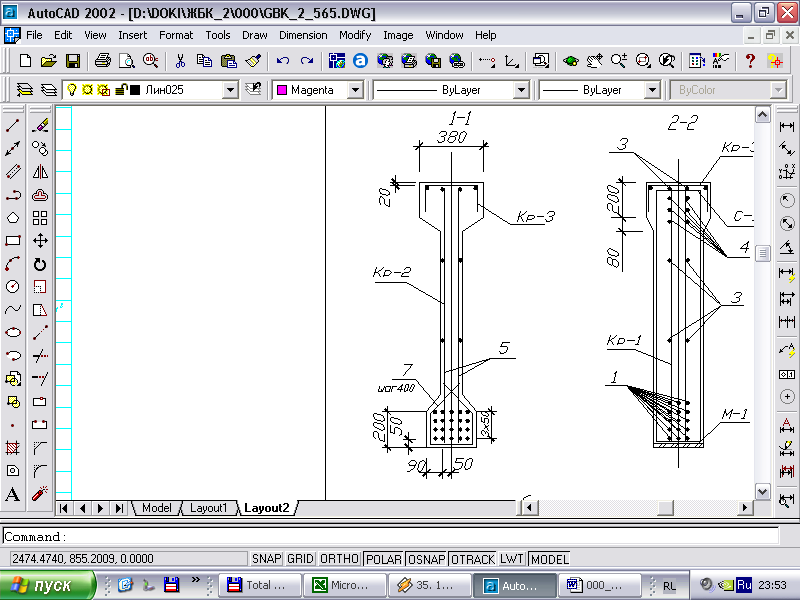
Рисунок 3.3 – Размещение предварительно-напряжённой арматуры.

3.4 Определение геометрических характеристик приведенного сечения балки

n = E_s/E_cm= 1800000/340000= 18000/3400 = 5,3.

Вычисление приведенной площади сечения балки A_п, поло­жения центра тяжести сечения у и момента инерции I_п сведено в таблице 9, где A_i и y_i — соответственно площадь сечения отдельного элемента и расстояние его центра тяжести от нижней грани балки; b_i и h_i — ширина и высота элементов сечения.

Таблица 3.2 – Вычисление геометрических параметров балки.

Ai, см2	yi, см2	Ai·yi, см3	y-yi, см	Ai·(y-yi), см3	, см4
(b’n-b)h’n=(38-12)24=624 (bn-b)hn=(28-12)25=400 bh=12·149=1790 nAn=5,3·19,81=105	h-0,5h’n=149-0,5·24=137 0,5hn=0,5·25=12,5 0,5h=0,5·149=74,5 a=12,5	85500 5000 133300 1300	77-137=-60 77-12,5=64,5 77-74,5=2,5 77-12,5=64,5	2245000 1663000 11200 436000	30000 21000 3310000 -
An=2919	Sn=∑Ai·yi=225100		-	∑=4355200	3361000
y=

Момент сопротивления приведенного сечения для его нижней растянутой грани при упругой работе материалов

W_o = I_п/y=7 716 200/77 = 100 200 см³.

Момент сопротивления для верхней грани балки при упру­гой работе материалов W_o = I_п/(h-y)=7 716 200/(149-77) = 107000 см³.

Момент сопротивления сечения для его нижней грани с учетом неупругих деформаций бетона

W_т = [0,292 + 0,75 (y₁ + 2·μ·n)+0,075 (y'₁ + 2 μ'·n)]·b·h².

В этой формуле:

y₁= (b_n-b)/(b·h)·h_n=(28-12)/(12·149)·25 = 0,223; n = 5,3;

y'₁=2·(b'_n-b)/(b·h)·h'_n=2·(38-12)/(12·149)·24=0,7;

μ=A_ser/(b·h) = 26,89/(12·149)=0,0150; μ'=0.

W_т = [0,292 + 0,75 (0,223 + 2·0,0150·5,3)+0,075(0,7+0)]·12·149²=168105,97см³

Момент сопротивления, с учетом неупругих деформаций для верхней грани балки,

W'_т = [0,292 + 0,75 (y₁ + 2·μ·n)+0,075 (y'₁ + 2 μ'·n)]·b·h².

В этой формуле:

y₁= (b'_n-b)/(b·h)·h'_n=(38-12)/(12·149)·24 = 0,35; n = 5,3;

y'₁=2·(b_n-b)/(b·h)·h_n=2·(28-12)/(12·149)·25=0,446;

μ'=A_ser/(b·h) = 19,81/(12·149)=0,0103; μ=0.

W'_т = [0,292 + 0,75·0,35+0,075 (0,446 + 2·0,0103·5,3)]·12·149²=158818,45см³

Расстояние от центра тяжести приведенного сечения до верхней ядровой точки (границы ядра сечения)

r^в_я=0,8W_o/A_п=0,8·100200/2919=27,5см;

до нижней ядровой точки

r^н_я=0,8W'_o/A_п=0,8·107000/2919=29,4см;